折叠尾翼驱动扭簧参数优化及数值仿真

蔡德咏，马大为，朱忠领，任 杰

(1.南京理工大学 机械工程学院，南京 210094;2.中国人民解放军71897部队，河南 信阳 464194)

无人机箱式发射技术将无人机贮存、运输和发射等功能系统地结合在一起，是实现无人机的机动性、可操作性和可维护性等要求的最佳方式［1，2］，因此得到广泛应用，如:美国的“鸬鹚”、俄罗斯的“图-141”、以色列的“哈比”、德国的“布雷维尔”都采用了箱式发射技术。为了适应箱式发射，减小发射装置尺寸，出现了折叠式尾翼［3］。折叠式尾翼的功用是:在通常情况下，先将尾翼折叠与发射箱内壁相适应，将无人机装入发射箱中。当无人机发射离箱后，尾翼即在展开力作用下自动展开并且锁定，达到设计规定的技术要求。

折叠尾翼设计中参数的确定，如驱动扭簧的刚度、尾翼折叠时刻的扭簧预扭转角的确定，是设计中的关键问题。以往的设计往往是通过动力学仿真或试验来确定折叠机构的设计参数，要想获得比较好的设计参数，得经过多次的计算或试验，通常这种方法获取的参数很难使折叠尾翼的性能达到最优［4］。针对这个问题，文中通过折叠尾翼的动力学分析，根据尾翼展开机构的设计要求及扭簧的设计准则，建立驱动扭簧参数的优化模型，利用Visual Basic语言编写程序，运用模拟退火算法优化得到扭簧参数，并通过数值仿真验证了优化结果。

1 折叠尾翼展开机构动力学模型

本文以某类箱式发射无人机扭簧驱动折叠尾翼展开机构为研究对象，该类尾翼属于扭簧力作用部分翼横向折叠式尾翼，结构如1所示，折叠尾翼由连接机身的内翼、外翼、驱动扭簧等部分组成。无人机在发射箱内时，外翼折叠，由发射箱内壁限位;发射离箱后，外翼在扭簧产生的扭矩驱动下绕旋转轴转动实现展开到位，锁紧装置将外翼锁定，完成展开过程，无人机转入正常飞行姿态。

折叠尾翼展开机构可视为理想约束系统，系统运动微分方程为:

图1 折叠尾翼机构示意图Fig.1 Folding empennage mechanism schematic diagram

式中:J为外翼绕转轴的转动惯量;为外翼绕转轴的展开角加速度;k为驱动扭簧刚度;θ为外翼的展开角度;φ为外翼折叠状态扭簧的预扭转角;m为外翼的重量;g为重力加速度;L为外翼质心a到转轴中心o的距离;M1为气动阻力矩;M2为摩擦力矩。

式(1)可以转化为标准的Runge-kutta格式进行求解，选取时间为自变量，以折叠外翼展开角度、角速度为变量，变量的初值为θ(0)=0、θ'(0)=0，建立常微分方程组，如式(2)所示:

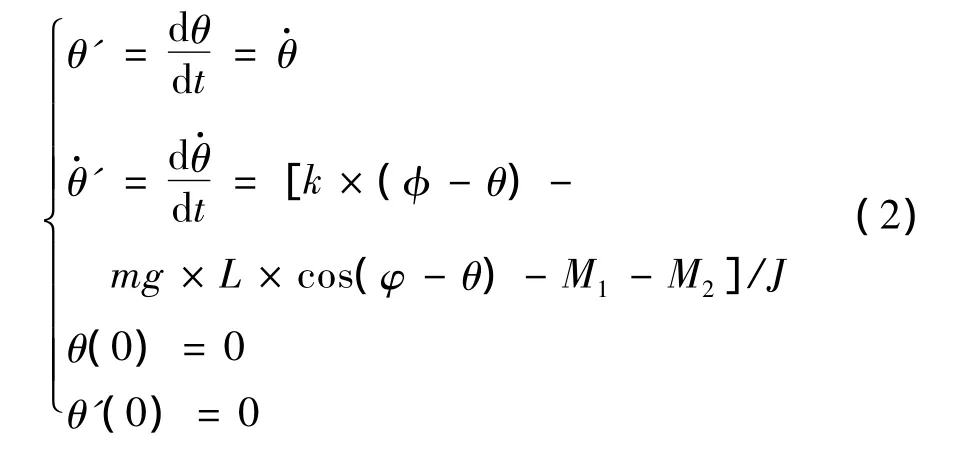
式中φ为外翼的设计折叠角。

用Visual Basic语言编制四阶Runge-kutta计算程序，选取合适的步长，即可以得到外翼展开角度θ、角速度随展开时间t变化的运动规律。

2 优化设计模型

2.1 设计变量

折叠尾翼展开机构中的扭簧是提供外翼展开到位的动力源，扭簧的参数、外翼折叠状态扭簧的预扭转角与外翼展开运动特性直接相关，通过合理选择扭簧参数和预扭转角即可得到合适的展开特性。根据折叠尾翼展开机构的设计要求、结构状况及扭簧的设计准则，选定扭簧的簧条直径d、扭簧中径D和有效圈数n和外翼折叠状态扭簧的预扭转角φ为优化设计变量，即:

2.2 目标函数

外翼展开到位瞬间，过大的冲击会影响无人机飞行姿态，也可能造成一些零件失效。在保证外翼正常打开的前提下，应使冲击载荷尽可能小［5，6］。碰撞过程复杂，冲击载荷难以直接计算，但外翼对内翼的冲击载荷大小与外翼展开到位时刻具有的动能大小密切相关。展开到位时刻动能越小，对内翼的冲击载荷越小，所以选取外翼展开到位瞬间动能最小为目标函数，即:

式中:E为外翼展开到位时具有的动能，而外翼的动能即为扭簧在外翼展开过程中克服重力矩、气动阻力矩、摩擦力矩做的功，所以E的计算式为:

式中扭簧刚度k可由扭簧参数计算得到:

2.3 约束方程

根据折叠尾翼展开机构的设计要求、结构状况及扭簧的设计准则［7］，得到约束条件:

(1)展开角度要求

外翼应能展开到位，式(2)计算得到的最大展开角度应满足设计要求:

式中θmax为计算得到的最大展开角度。

(2)展开时间要求

为了保证无人机能迅速转入飞行姿态，外翼的展开时间不能太长。展开时间应满足设计要求:

式中t(φ)为计算得到的外翼展开到位时间;［t］为设计允许的最大展开时间。

(3)扭簧的几何条件

选用碳素弹簧钢丝为材料(GB4537-1989)，簧条直径d、扭簧中径D、旋绕比C=D/d应满足扭簧的设计准则(GB1358-78)，并符合尾翼转轴的空间尺寸。

(4)扭簧的稳定性条件

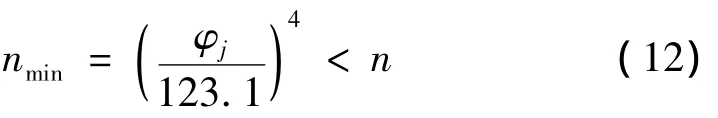
式中φj为扭簧极限扭转角，根据下式计算:

式中Tj为扭簧工作极限扭矩;σj为扭簧极限弯曲应力(σj=0.8σb，σb为弹簧钢丝的抗拉极限强度。);K1为扭簧的曲度系数，根据下式计算。

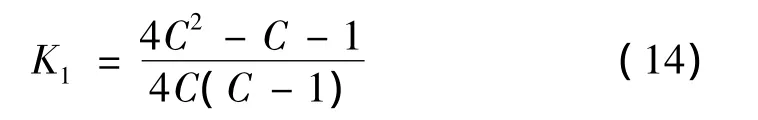
(5)扭簧强度条件

式中Tn为扭簧工作中最大扭矩，即外翼折叠状态扭簧的扭矩。σBp为许用弯曲应力，σBp=0.8σb。

(6)扭簧质量条件

考虑在无人机上使用，质量不应过大，文中约束优化后扭簧的质量应不大于原方案的质量。

式中m0为原方案的扭簧质量，m0=π2D0n0ρ/4，ρ为扭簧钢丝材料的密度。

(7)扭簧自由长度条件

扭簧的自由长度应满足尾翼转轴的结构情况。

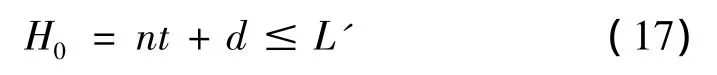
式中H0为扭簧自由长度，t为节距(t=d+0.5)，L'为尾翼转轴空间允许的扭簧最大长度。

综上所述，扭簧参数优化的数学模型为:

3 优化分析

选用模拟退火算法作为优化算法，运用Visual Basic语言编制计算程序，建立尾翼展开机构的扭簧优化求解框架，优化扭簧参数。

3.1 模拟退火算法

模拟退火算法［8，9］(Simulated Annealing，简称 SA)是基于Monte Carlo迭代求解策略的一种随机寻优算法，其出发点是基于物理退火过程与组合优化之间的相识性，SA由某一较高温度开始，利用具有概率突跳特性的Metropolis抽样策略在解空间中进行随机搜索，伴随温度的不断下降重复抽样过程，最终得到问题的全局最优解。模拟退火算法的基本步骤:

(1)给定初始温度t=t0，确定降温准则，并随机产生初始状态s=s0，令初始最优解为si=s*=s0，令k=0;

(2)判断是否满足优化结束的收敛条件，如果满足则输出优化的结果，不满足继续步骤(3);

(3)由状态产生函数得到新状态sj，即sj=Generate(s)，并计算路程目标的增量值，设路程目标函数为C(x)，则增量ΔCj=C(sj)-C(si);

(4)判断ΔCj的值。如果ΔCj＜0，则接受sj为当前解，即si=sj，并判断C(sj)＜C(s*)是否成立，如果正确令s*=sj;如果 ΔCj＞0，判断条件 min{1，exp［-ΔCj/tk］}≥random［0，1］是否满足，如果满足同样接受sj为当前解，即si=sj，如果不满足则保持当前状态不变;

(5)判断是否满足Metropolis抽样稳定性准则，如果满足则转到步骤(2)，并令k=k+1，tk+1=update(tk);如果不满足则转到步骤(3)。

模拟退火法是一种全局优化算法，它可以有效地避免寻优过程过早收敛于局部最优值的问题，利用该方法求得的结果至少是准最优解。

3.2 优化求解框架

尾翼展开机构的扭簧优化求解框架如图2所示，用Visual Basic语言编制计算程序，首先读入簧条直径d、扭簧中径D、有效圈数n和扭簧的预扭转角φ等参数，求解折叠尾翼展开机构的运动微分方程并得到外翼展开角度θ、角速度θ·随展开时间t变化的运动规律，同时计算约束方程，判断是否满足也是条件。满足约束条件则进行目标函数计算，运用模拟退火算法优化，直到收敛到最优解，得到最优方案。

图2 优化求解框架Fig.2 Optimal solving frame

3.3 结果分析

按照优化求解流程，输入折叠尾翼展开机构初始方案的参数:簧条直径d0、扭簧中径D0、有效圈数n0和扭簧的预扭转角 φ0，即X0=［d0，D0，n0，φ0］T，经过5852 次运算，获得了最优解X=［1.4d0，1.07D0，0.46n0，0.28φ0］T。如表1 所示，与原方案相比，优化后的方案扭簧质量没有增加，展开时间没有增大，而外翼展开到位时动能减小了82%。

4 仿真分析

基于几何模型的数值仿真方法，不仅能够形象直观地分析机构运动过程，还可获得所关心的冲击载荷，检查设计合理性［10-12］。本文采用有限元分析软件ABAQUS建立了无人机的有限元模型，利用显式动力学方法求解外翼展开的运动规律和冲击载荷，检验优化结果。

表1 优化前后参数比较Tab.1 Comparison of the original and optimized design parameters

4.1 有限元模型

按照折叠尾翼各构件的几何尺寸和相互位置关系建立几何模型，赋予材料属性，使外翼的质量、质心位置、绕旋转轴的转动惯量等参数与设计值吻合。外翼与内翼之间利用Hinge连接单元建立连接关系，释放绕旋转轴的旋转自由度，并在旋转轴处建立扭簧约束。外翼与内翼的碰撞面由两部分构成，两两之间分别建立接触约束关系。根据已知参数在模型中加载重力、气动阻力矩、摩擦阻力矩。

外翼展开到位时存在碰撞冲击，动态分析时采用集中质量公式的线性单元模拟应力波的效果优于采用一致质量公式的二次单元［13］，所以网格单元都选用线性单元。根据构件的结构特点，内翼和外翼的碰撞面等部分用8节点实体单元划分网格，外翼的蒙皮部分用4节点壳单元划分网格。为了提高获取冲击载荷的精度，增加外翼和内翼碰撞面的网格密度。折叠尾翼的有限元模型如图3所示。

图3 折叠尾翼有限元模型Fig.3 Finite element model of folding empennage

4.2 比较分析

在有限元模型中，根据展开机构优化前后的扭簧刚度和外翼折叠状态扭簧的预扭转角，定义驱动扭簧扭矩和展开角的关系。仿真计算，得到了外翼动能时间曲线、展开的角位移时间曲线、两处碰撞面的冲击载荷(合力)时间曲线分别如图4-图6所示。

结合表1和图4-图6可以看出:优化过程中理论计算得到的优化后方案外翼展开到位的动能为0.18E0，展开时间为0.92t0。有限元仿真计算得到的这两项值分别为0.17E0和0.89t0，误差都不超过4%，验证了优化结果。

进一步分析可以看出:优化前扭簧预扭转角φ0大于外翼折叠角φ，在外翼展开过程中扭簧始终做正功，外翼不断被加速，动能不断增大。虽然可以在较短的时间内展开到位，但到位的冲击载荷比较大。优化后驱动扭簧预扭转角为0.28φ0，小于外翼折叠角φ，但由扭簧参数计算可知扭簧刚度很大，在外翼的展开的初始阶段以较大的扭矩让外翼加速，动能增加比较快，在保证外翼获得足够的动能展开到位后，扭簧施加一个反向的扭矩，开始做负功，外翼转动动能开始减小，到位时刻已经减小到一个较小值。所以优化方案的展开时间没有增长，而冲击载荷最大值仅为原方案的23.2%，很好的改进了尾翼展开机构的性能。

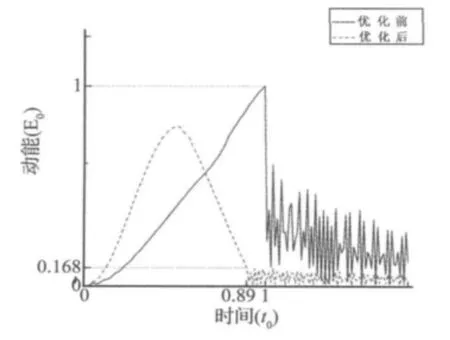
图4 动能时间曲线Fig.4 The time curve of kinetic energy

图5 角位移时间曲线Fig.5 The time curve of angular displacement

图6 冲击载荷时间曲线Fig.6 The time curve of impact load

5 结论

本文根据尾翼展开机构的设计要求、结构状况及扭簧的设计准则，建立驱动扭簧参数优化模型。采用模拟退火算法，用Visual Basic语言编制程序优化得到驱动扭簧的优化参数。运用有限元仿真软件建立了折叠尾翼机构的动力学模型，形象直观地分析机构展开运动过程，比较了优化前后方案的动力学性能。结果表明:

(1)通过建立折叠尾翼展开机构的动力学模型，可根据设计要求和结构条件及扭簧设计准则建立优化模型得到使系统性能最优的扭簧参数，大大提高了设计效率。

(2)应用有限元数值仿真方法，能够形象直观地分析折叠尾翼展开机构运动过程，有效掌握折叠尾翼运动特性和冲击响应。

(3)本文的研究对折叠尾翼展开机构的优化设计和完善具有重要的理论指导意义。

［1］郭小良，裴锦华，杨忠清，等.无人机折叠机翼展开运动特性研究［J］.南京航空航天大学学报.2006，38(4):438-441.

［2］ Kroyer R.Wing mechanism analysis［J］.Computers and Structures.1999，72:253-265.

［3］ Henry JI， SchwartzD R， Soukup M A. Design，construction，and testing of a folding-wing，tube-launched micro air vehicle［R］.AIAA 2005-1451.43rd AIAA Aerospace Sciences Meeting and Exhibit，10-13 January 2005，Reno，Nevada.

［4］秦兵才，文立华.小型折叠弹翼展开机构优化设计［J］.弹箭与制导学报，2009，4:206-208.

［5］张凡立，张美艳，唐国安，等.太阳能电池阵地面展开试验的仿真技术［J］.振动与冲击，2007，26(7):43-45.

［6］王华光，王 华.巡飞器折叠翼的设计要求［J］.飞航导弹，2009，6:36-39.

［7］成大先.机械设计手册(第七篇弹簧)［M］.北京:化学工业出版社，2004:44-47.

［8］Suman B.Study of simulated annealing based algorithms for multiobjective optimization of a constrained problem ［J］.Computersand ChemicalEngineering，2004 (28):1849-1871.

［9］Geng X T.A simple simulated annealing algorithm for the maximum clique problem ［J］.Information Sciences.2007(177)5064-5071.

［10］ Reich G W，Bowman J C，Frank G J.Development of an integrated aeroelastic multibody morphing simulation tool［R］.AIAA 2006-1892.47th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Con，1-4 May 2006，Newport，Rhode Island.

［11］ Lee D H，Chen P C.Nonlinear aeroelastic studies on a folding wing configuration with free play hinge nonlinearity［R］.AIAA 2006-1734.47th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Con，1-4 May 2006，Newport，Rhode Island.

［12］ Scarlett J N，Canfield R A.Multibody dynamic aeroelastic simulation of a folding wing aircraft［R］.AIAA 2006-2135.47thAIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，and Materials Con，1-4 May 2006，Newport，Rhode Island.

［13］石亦平，周玉容.有限元分析实例详解［M］.北京:机械工业出版社，2006，60-62.