输电塔气弹模型制作及风雨荷载的相似比研究

唐顺勇，李宏男

(1.中国联合工程公司，杭州 310022;2.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116024)

近年来，随着国民经济的迅速发展、科学技术的进步和环保意识的增强，电力工业作为经济建设和人民生活的支柱产业正发生着巨大的变化［1］，输电塔的建设速度和规模都达到了前所未有的程度，刚建成的高370m的舟山大跨越塔就是其中一例。输电塔的轻质、高柔和阻尼小等特性，使其主要的控制荷载为风荷载，由于强风雨荷载的作用，对输电塔造成的破坏及次生灾害时常发生［2］。

风工程的研究方法主要有以下三种:现场实测、风洞试验以及理论计算。由于无法在理论上完善地解决风振问题，因此通过气动弹性模型的风洞试验测定风致振动响应仍是目前最常用的方法［3］。要准确评价气弹模型的风致振动响应，气弹模型的精确制作是关键。梁正平等［4］以向家坝上海的800 kV特高压直流线路为例，考虑铁塔模型刚度和气动反应两方面的情况，提出以半刚性模型节段加“U”型弹簧片的方法制作铁塔弹性模型;韩银全等［5］采用昌西到南昌的500 kV输电塔线体系为原型，保证气弹模型与原型塔刚度、质量和阻尼等严格相似，介绍了完全气弹模型的制作过程;付国宏等［6］等以杭州瓶窑500 kV输电线路为原型，制作了气弹模型并进行了架空输电线路风振试验研究。

基于风雨荷载(暴风雨)作用下输电塔线体系风振响应分析的研究还较少。国内外学者对相似理论方面已经做了大量的研究，但是对于雨荷载相似问题的研究还处于起步阶段。石启印等［7］利用相似理论分析了首都机场新塔台结构气动弹性模型风洞实验的相似准则，得到了塔台结构气动弹性模型的相似参数及模型参数的缩尺率。陈星烨等［8］以岳阳洞庭湖大桥模型为例，推导了相似判据以及模态参数的相似比。但是目前对于雨荷载相似问题的研究还鲜见报道。

本文详细介绍了风洞试验中气弹模型的制作方法，以及风洞试验中风雨荷载缩尺问题的理论研究，为以后研究风雨荷载对输电塔的影响提供了理论依据。

1 相似准则

风洞试验的相似性要求一般通过保持模型和原型之间一些对应的由单值条件组合的无量纲参数一致性来得到满足。通过相似准则的量纲分析法，可得出气弹模型风洞试验所要求的相似准则。根据各相似准则［9］，既要保证模型与原型的几何相似、刚度相似，还要保证模型与原型间的6个无量纲相似参数相等，分别是惯性参数(密度比)、Strouhal数、弹性参数(Cauchy数)、重力参数(Froude数)、雷诺数(Reynolds数)和阻尼参数.就目前的技术条件而言，要对模型进行完全气弹模拟是相当困难或是难以实现的，所以只能进行部分模拟。因此，在输电塔线体系风洞试验中，根据实际情况、试验条件以及所要研究问题的性质选取一些至关重要的相似准则，而放弃一些次要的或难以模拟的相似准则。

实际上，有些无量钢参数的相似性可能是互不相容的，比如Reynolds数和Froude数就是相互矛盾的，Reynolds数反映的是惯性力和粘性力的比值关系，在低速风洞内Reynolds数相似参数是很难模拟的，常被放弃;Froude数是反映重力与惯性力的比值关系，对于输电塔气弹模型风洞试验，重力参数是必须要满足的;Strouhal数反映了模型的固有频率和几何缩尺比之间的关系，是风洞试验必须满足的相似准则。

2 气弹模型制作

2.1 工程概况

本次风洞试验的气弹模型是以某500 kV高压输电塔为原型，塔高为78 m，主材为角钢的格构式直线塔SSJ1T，呼高为45 m，水平档距为400 m。铁塔示意图如图1所示。

图1 直线塔SSJ1TFig.1 Straight-line tower SSJ1T

2.2 模拟方法

输电塔气弹模型模拟刚度的方法通常有2种:集中刚度法和离散刚度法［10］.集中刚度法是分别模拟模型的刚度和几何外形。用铜管之类的材料来模拟刚度，用ABS板来模拟模型的几何外衣。离散刚度法是将输电塔的各个杆件看作二力杆，只模拟轴向刚度来模拟整个模型的刚度。这种方法制作的模型很难保证在各个杆件刚度和几何尺寸相似的情况下，做到模型的整体刚度和质量的严格相似。

考虑到原型塔的高度、风洞的高度以及模拟紊流边界层尺寸等要求，模型几何的相似比定为1∶45。塔模型的高度为1.73m，采用空心的黄铜管来模拟塔架的刚度.采用轻质的ABS板来模拟外衣.模型的相似参数见表1所示。

表1 模型的相似系数(n=45)Tab.1 Model of the similarity coefficient(n=45)

为真实反映输电塔各部位对整体塔架的动力特性的贡献，对于高柔的输电塔结构，气弹模型应该与原型塔刚度、质量等分布相似，这是气弹模型设计与制作的关键［11］。输电塔的各个杆件可以看作是二力杆，用空心铜管来模拟拉伸刚度SEI=1:n3，通过铅丝配重来模拟质量相似比Sm=1:n3，又因为符合几何相似比，所以体积也是相似的，进而保证了密度的相似比为1。

输电塔的杆件截面种类很多，有些截面尺寸差别很小，相对于模型制作中的误差，这些差别是可以忽略不计的，因此在实际制作时对杆件进行归并，使制作过程相对简单，归并后的杆件型号如表2所示。

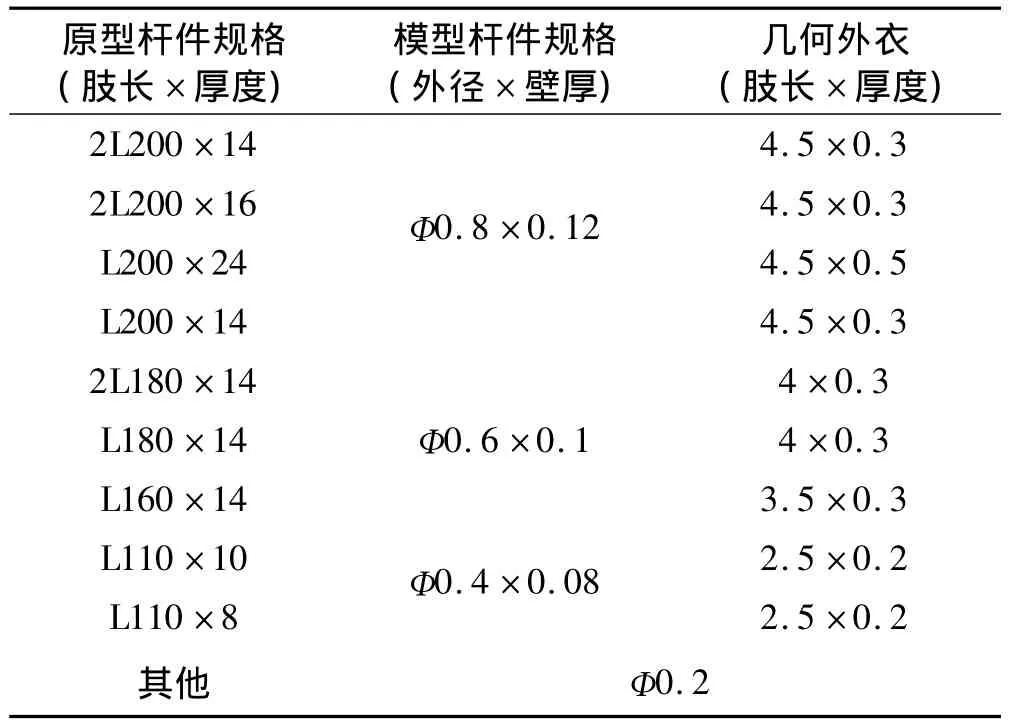
表2 输电塔构件规格(mm)Tab.2 Member size of transmission tower (mm)

本试验只关注单塔的风雨致振动力试验，所以并未进行输电线和绝缘子的模拟。单塔模型如图2所示。

2.3 动力特性计算与标定结果对比

气弹模型制作完成后，我们对整个模型进行模态实测。在输电塔模型上装小型加速度传感器，并用自由激振法测得模型的加速度时程，然后对数据进行FFT处理，得到自振频率。

表3给出了SSJ1T塔的自振频率原型计算值、模型期望值以及模型的实测值。可以发现，前2阶频率相对误差在6%以内，模型设计精度较高;第3阶频率识别不明显，故未列出来。各阶模态的阻尼比均在0.1% ～0.2%之间，符合模型设计要求。

图2 直线塔SSJ1T模型图Fig.2 Model of SSJ1T for the straight-line tower

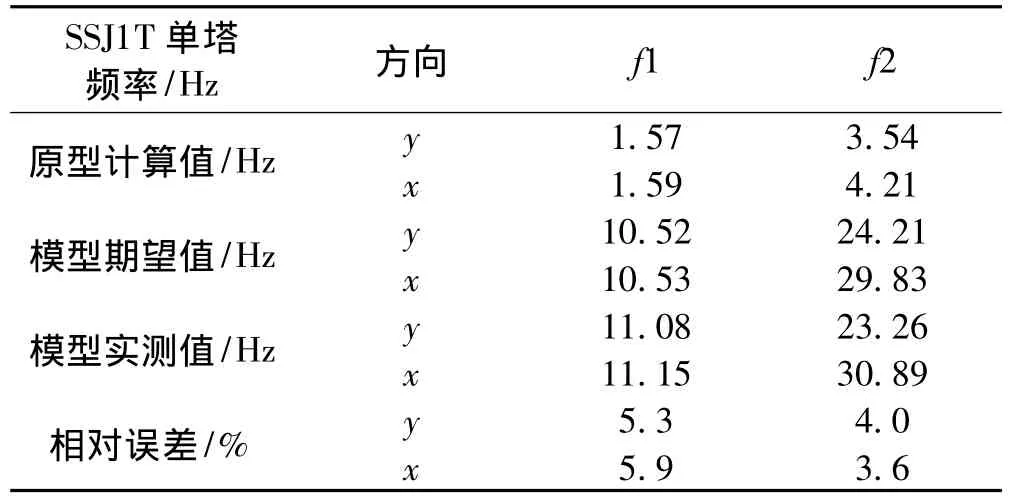
表3 模型自振频率测试结果Tab.3 Natural frequencies of experment model

3 风雨荷载的缩尺比

目前，对于风荷载的缩尺比已经有了比较成熟的计算公式，但是对于雨荷载缩尺目前还没有这方面的资料做详细论述。

3.1 理论依据

根据相似准则量纲分析法，可得出各相似参数。

根据弗劳德数一致性条件，也称为重力相似，所以对模型和原型来说，Fr=1.0。我们可以得到:

式中，V为物体运动速度;g为重力加速度;D为物体的特征长度;以下所有字母的下标m代表模型，p代表原型。

又对于重力加速度g而言:

式中，λg为重力相似比;g为重力加速度。可以推演出:

式中，λv为风速缩尺比;λL为几何缩尺比:

考虑雷诺数一致性条件时:

式中，ρ为流体的密度;μ为泊松比:

即可以得到:

对于低速风洞［12］，由于雷诺数的一致性条件是一般不可能得到满足的，常被忽略。因此，对于风速的缩尺比，采用考虑弗劳德数Fr一致性而得到公式(3)。

3.2 导出缩尺比

各种物理量的缩尺比并不是完全独立的。大多数物理量的缩尺比可根据一些基本缩尺比通过量纲分析导出。比如，力的缩尺比λF:

式中，λF为力的缩尺比;λM为质量缩尺比;λa为物体的加速度缩尺比。

而力的缩尺比也可以这样定义:

式中，λP为压强缩尺比;λs为面积的缩尺比。由以上式(6)和(7)可得到:

也就是说，压强的缩尺比等于几何缩尺比。

3.3 验证风速缩尺比

上文得到的压强缩尺比等于几何缩尺比的结论，是通过一般荷载得到的，那么对于对风荷载也同样是成立的，即:

式中，λP(w)为风荷载的压强缩尺比;ρ为空气密度;V为风速。

由式(9)可以得到:

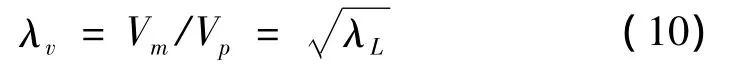
这与根据弗劳德数相似得到的公式(3)是一样的，即验证了我们推导过程的正确性。

3.4 雨荷载的缩尺

既然我们导出的力的缩尺比适应于任意荷载，那么对于雨荷载同样是成立的。对雨荷载而言:

式中，λP(r)为雨荷载的压强缩尺比。

雨滴在与结构碰撞的极短时间内速度变为零，这符合动量守恒定律，雨滴与结构之间的相互作用过程遵循牛顿第二定律［13］。雨滴在时间τ内对结构的撞击力F(τ)为:

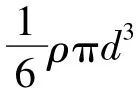
要把雨滴作用在结构上，需要将单个雨滴的冲击力转化为均布荷载Fd(N/m)为:

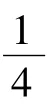
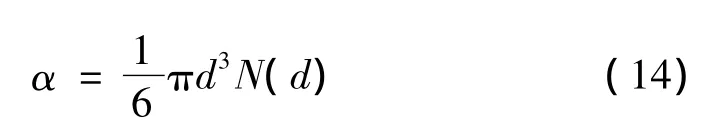
式中:N(d)为单位体积空气中直径为d(mm)的雨滴个数。

可以得出［14］:

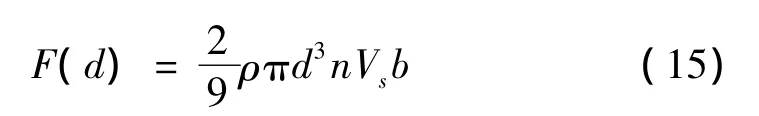
在实际计算时，对于结构受到的降雨冲击力可以分解成竖向冲击力和与顺风向冲击力;竖直方向，Vs取自由下落速度Vm;在顺风向，Vs取顺风向风速。

雨压计算公式为:

式中:Pr为雨荷载的压强;ρr为雨荷载的密度;d为雨滴直径，大约为0 mm-6 mm;n为雨滴数密度，即单位体积内雨滴个数;V为顺风向风速，即雨滴打到塔上的速度。

由公式(11)可以得出:

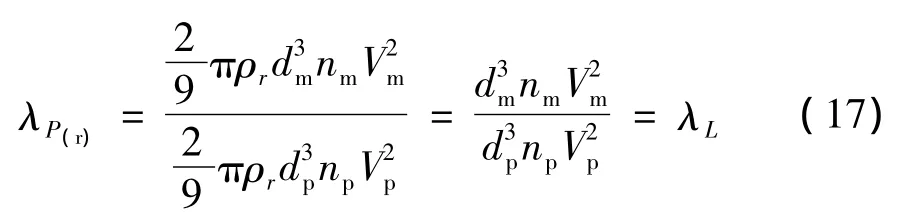
式中，λp(r)为雨荷载的压强缩尺比;ρr为雨荷载密度;d为雨滴直径;n为雨滴数密度;V为顺风向风速;下标m代表模型，p代表原型。

从上式可以导出:

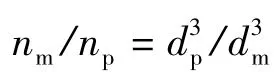
4 结论

本文在满足相似理论的基础上，介绍了高压输电塔气弹模型的制作方法。并进行了风雨荷载的缩尺比研究，得到了以下结论:

(1)本文介绍的气弹模型制作方法，在保证无量纲相似参数相等的前提下，既可满足质量相似和刚度相似，又可满足气动外形相似。按照本文方法制作的气弹模型符合设计要求。

(2)提出了雨荷载的压强计算公式，这是雨荷载缩尺公式的前提。

(3)通过模型和原型的雨压缩尺比等于几何缩尺比的关系，首次得到了雨荷载的缩尺公式，这为风洞试验中雨荷载的相似提供了理论依据。

(4)实际做风雨激励的风洞试验时，我们假设风洞中的雨滴直径等于自然界中的雨滴直径，得出了风洞中和自然界中的雨滴密度相等的结论，这为风洞试验中模拟雨荷载提供了可行依据。

［1］李宏男，白海峰.高压输电塔-线体系抗灾的研究现状与发展趋势［J］.土木工程学报，2007，40(2):39-46.

［2］ Li H N，Bai H F.High-voltage transmission tower-line system subjected to disaster loads［J］.Progress in Natural Science，2006，16(9):899-911.

［3］Loredo-Souza A M ，Davenport A G.A novel approach for wind tunnel modeling of transmission lines［J］ .Journal of Wind Engineering and Industrial Aerodynamic，2001，6(89):1017-1029.

［4］梁政平，李正良.特高压输电塔线体系的气动弹性模型设计［J］.重庆大学学报，2009，32(2):131-136.

［5］韩银全，梁枢果，邹良浩，等.输电塔线体系完全气弹模型设计［A］.第十三届全国结构风工程学术会议论文集(上册)［C］.大连:中国土木工程学会，2007，260-265.

［6］付国宏，程志军，孙炳楠，等.架空输电线路风振试验研究［J］.流体力学实验与测量，2001，15(1):15-21.

［7］石启印，李爱群，杜东升，等.首都机场新塔台模型风洞模拟相似理论分析［J］.特种结构，2004，21(1):47-49.

［8］陈星烨，马晓燕，宋建中.大型结构试验模型相似理论分析与推导［J］.长沙交通学院学报，2004，21(1):11-14.

［9］邓洪洲，朱松晔，陈晓明，等.大跨越输电塔线体系气弹模型风洞试验［J］.同济大学学报，2003，31(2):132-137.

［10］郭 勇，孙炳楠，叶 尹.大跨越输电塔线体系气弹模型风洞试验［J］.浙江大学学报(工学版)，2007，41(9):1482-1486.

［11］李宏男，王前信.大跨越输电塔体系的动力特性［J］.土木工程学报，1997，30(5):28-36.

［12］Barlow J B，Rae Jr W H，Pope A.Low speed wind lowtunnel testing［M］.New York:John Willey ＆ Sons，INC，1999.

［13］李宏男，任月明，白海峰.输电塔体系风雨激励的动力分析模型［J］.中国电机工程学报，2007，27(30):43-48.

［14］任月明.风雨激励下输电塔线体系的动力响应分析［D］.大连:大连理工大学，2007.