基于结点6自由度的输电线舞动有限元分析

晏致涛，李正良，杨振华

(1.重庆大学 土木工程学院，重庆 400045;2.山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045)

覆冰导线在风荷载作用下可能作低频大幅自激振动，这种现象称为舞动。在2009年底至2010年初，河南、河北、湖北、湖南、山东、辽宁等13个省输电线路发生大面积导线舞动现象。舞动发生风速一般较低，幅值会达到垂度的数倍，所以舞动形成后对输电线路造成极大的破坏作用，导致电线相互碰撞、绝缘子损坏、金具破坏，严重时甚至使铁塔倒塌，发生大面积电力供应瘫痪［1］。

舞动发生时，导线会产生竖直、水平和扭转等复杂耦合振动。最早的输电线舞动分析理论是20世纪30年代 DenHartog［2］提出的垂直运动舞动理论，随后，Nigol提出了扭转舞动理论［3，4］，Haaker［5］用单(扭转)自由度模型进行了进一步分析，这几种舞动理论均为基于单自由度体系的解析分析。之后，一些学者进行了2自由度的导线舞动模型分析，如包括竖向和扭转运动的导线舞动的2自由度模型［6，7］及考虑了水平运动和仰俯运动的共同作用的2自由度模型［8］。在实际的野外观测中，导线的舞动是包含水平、竖直以及扭转等各个方向的振动。基于这种现象，Yu［9-11］建立了包含2个平动和1个扭转自由度的3自由度舞动分析模型。Desai［12］等人采用有限元的思想，提出了用3结点等参索单元建立结点3自由度模型研究导线的舞动。

基于3自由度的舞动分析模型得到了极大的发展，许多研究者结合具体工程实例进行了分析［14-18］。该类分析多数基于传统的索单元理论［19］。由于索单元理论一般均忽略抗弯刚度、抗扭刚度和抗剪刚度，多数学者均添加一个抗扭刚度来表征输电线的抗扭能力，采用McConnell［20］提出的耦合系数 BT考虑轴向和扭转的耦合刚度，在舞动分析的时候大都将该耦合系数取值为零。然而，Luongo［21，22］认为采用上述耦合系数简单地考虑轴向与扭转的耦合刚度是不合理的，并通过解析方法说明抗弯刚度对扭转刚度的影响不可忽略，全面考虑抗弯、抗拉刚度以及抗扭刚度是非常有必要的。

在Zhu［23］提出的空间曲梁插值函数的基础上，笔者考虑了导线运动过程中的扭转非线性以及覆冰产生的偏心惯性作用，提出了结点6自由度覆冰输电线舞动分析模型，建立了模拟覆冰导线舞动的基于更新Lagrange格式的有限元方程，并进行了求解。由于考虑了抗弯刚度、抗拉刚度与抗扭刚度的影响，该模型能更加准确地描述输电线的各自由度耦合舞动行为，有助于阐明导线舞动的发生机理。

1 覆冰导线有限元模型

输电线分析模型及坐标系如图1(a)所示，Kx、Ky、Kz分别表示输电线两端绝缘子和输电塔在x，y，z方向上的边简化界条件。图1(b)为输电线的断面形式，由于覆冰后，导线截面的质心移至P点。图1(c)为空间坐标系下的3结点覆冰输电线索梁单元。每个单元是位于局部随转坐标系，每个结点有6个自由度——x，y，z方向的平动和转动。

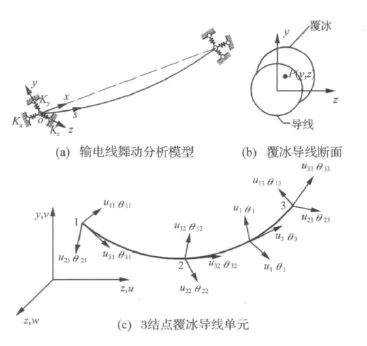
图1 输电线及3结点覆冰导线模型Fig.1 Model of transmission lines and three-node iced cable

1.1 位移插值函数

3结点6自由度覆冰输电线的有限元模型位移插值函数可以参考曲梁理论［23］，按多项式构造，可得t时刻单元位移向量:

式中，κ为单元的曲率，下划线为含曲率的项。若曲率为零，则该插值函数对应普通直梁单元。根据图1(c)中坐标系及符号表示，令结点位移ue={u11u21u31θ11θ21θ31u12u22u32θ12θ22θ32u13u23u33θ13θ23θ33}T，单元内部任一点位移为u={u1u2u3θ1θ2θ3}T，则式(1)可以写成位移插值的矩阵形式，有:

式中，A为式(1)多项式插值的系数矩阵，Tr可由位移插值函数代入各结点位移求得，显然，3结点6自由度单元模型的型函数为ATr。

1.2 曲率—位移关系

在图1(c)中随转坐标系下，忽略索的剪切变形，考虑轴向、两个方向的弯曲以及扭转变形，其应变-位移关系为:

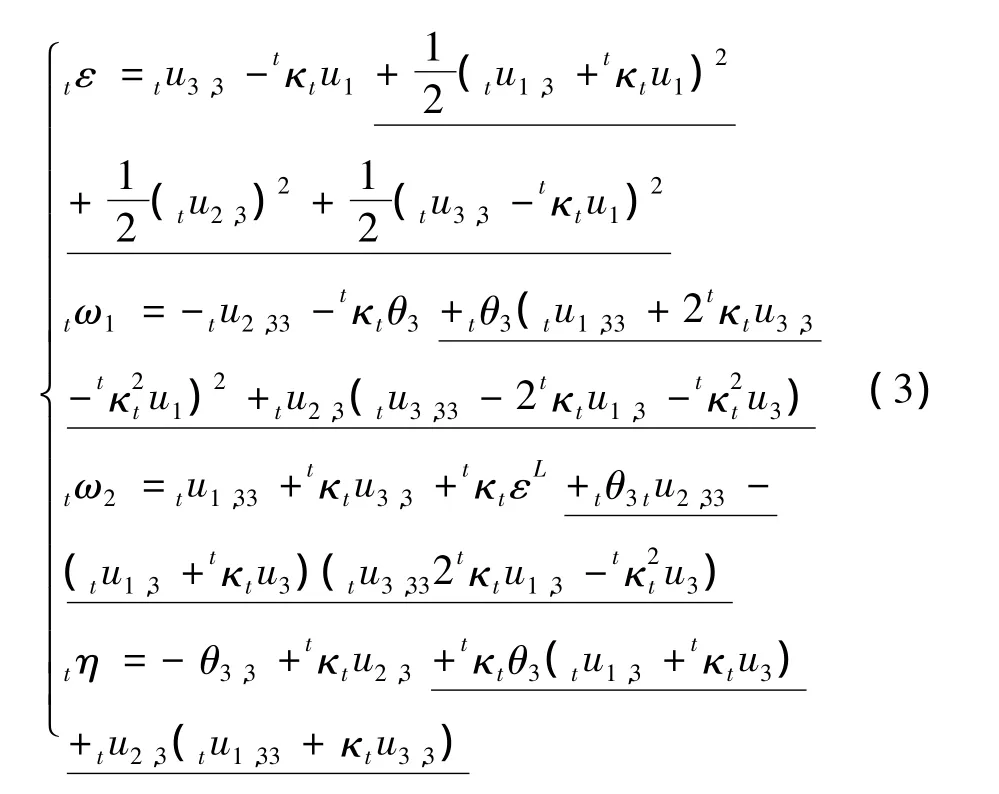
式中:下标中“，”表示求导;ε为轴向应变;φ1为局部坐标系下u1方向弯曲曲率;φ2为局部坐标系下u2方向弯曲应变;η为局部坐标系下u3方向扭转应变;下划线部分表示应变的非线性部分。从应变可见，扭转应变与轴向变形也有关。

2 覆冰导线舞动的有限元方程

根据Hamilton原理，并考虑输电线的阻尼力，可以得到运动方程:

式中tM、tK、tC为t时刻的质量、刚度与阻尼矩阵，t+ΔtF 为t+Δt时刻的荷载向量。

2.1 单元质量矩阵

图1(b)所示的覆冰输电线上的一个横截面在局部坐标系下x，y，z方向的质量密度矩阵为μ，则空间3结点覆冰输电线单元的一致质量矩阵为:

式中，上标“e”表示单元，Ar为截面面积;Sy为截面对y轴的静矩;Iy为截面对y轴的惯性矩;Iz为截面对z轴的惯性矩;J为截面对形心的极惯性矩。质量密度矩阵μ中，Sy和Sz以及极惯性矩J可以沿输电线长度s方向改变。

2.2 单元刚度矩阵

在局部坐标系下建立单元刚度矩阵Ke:

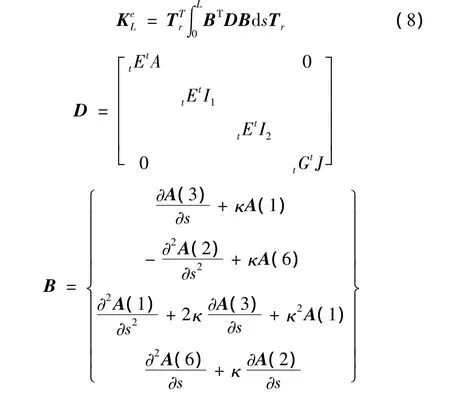
式中，tE、tG分别为t时刻的弹性模量和剪切模量，矩阵A括号里的数字表示行向量。

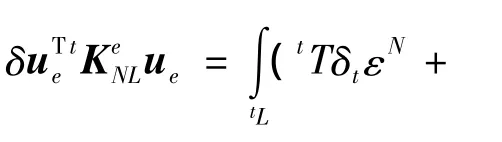
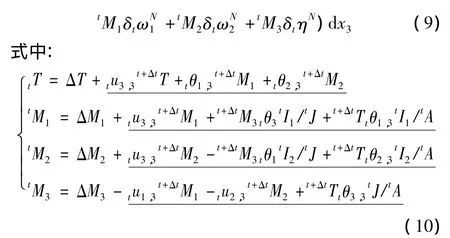
式中，ΔT、ΔM1、ΔM2、ΔM3分别为轴力及力矩的线性增量，可以通过线性刚度表达式(8)乘以变形增量求得。从式中可见，轴力、弯矩以及扭矩是相互耦合的，并且扭矩是非线性的。

式中，g为重力加速度，Sz为覆冰输电线对z轴的静矩;diag为取对角阵符号。

2.3 单元阻尼矩阵

采用瑞利阻尼，表达式为:

式中，αv、βv为瑞利阻尼系数。

2.4 单元荷载向量

作用在导线上的引起舞动的空气动力与作用在其他结构上的常见荷载不同。气动力依赖于覆冰导线的几何非线性和风攻角α。通过覆冰导线的风洞试验，测量得到的对应于攻角α的阻力系数C1(α)、升力系数C2(α)和扭矩系数C3(α)，进而计算得到升力F1、阻力F2和扭矩M3。单元荷载向量Fe可表示为:

式中，F1、F2、F3分别为局部坐标系三个方向上的结点力;M1、M2、M3分别为局部坐标系三个方向上的弯矩。ρair为空气密度;d为裸导线的直径;Vrel为相对风速，一般取Vrel≈Vw，Vw为作用在导线上的平均风速。

2.5 坐标转换矩阵

上述单元质量矩阵、单元刚度矩阵以及荷载列阵等是在局部随动坐标下推导出来的，在求解整体方程时，需要将它转换到整体坐标。从整体坐标矩阵至局部坐标矩阵的转换矩阵可以分两步完成，第一步将全局坐标系的x坐标轴旋转至输电线的弦长方向，y方向旋转至输电线的竖向，z方向旋转至输电线的侧向;第二步将输电线各个结点x，y，z方向旋转成图1(c)中的1、2、3方向，中间结点可以不旋转。

2.6 边界条件

在一跨导线档距两端边界处，既有远跨导线连接，又有绝缘子连接。边界处的刚度系为相应边界刚度与绝缘子刚度的叠加。其中x方向边界刚度系数为x方向刚度系数为绝缘子x方向摆动刚度系数与远跨导线x方向刚度系数相叠加。y方向刚度系数为绝缘子y方向摆动刚度系数，一般假定为无穷刚性。z方向刚度系数为绝缘子z方向摆动刚度系数与远跨导线z方向刚度系数相叠加。上述刚度组装叠加过程一直进行到耐张塔为止，即耐张塔处结点是铰接的。

3 动力平衡方程的求解

求解覆冰输电线非线性舞动动态问题的Newmark-β法的步骤归纳如下:

(1)计算Newmark-β法中a0-a7等8个积分参数。根据新的位形计算覆冰输电线单元的内力tT、tM1、tM2及tM3，根据式(8)～ 式(11)确定t时刻结构的刚度矩阵tK和新的有效刚度矩阵tK^:

(2)形成有效载荷向量

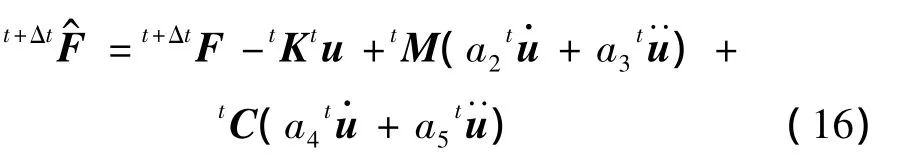
(3)求解位移增量

(4)在每一时间步内进行动力平衡迭代(Newton-Raphson平衡迭代)，求解第i次迭代位移增量的修正量，并计算修正后的位移增量:

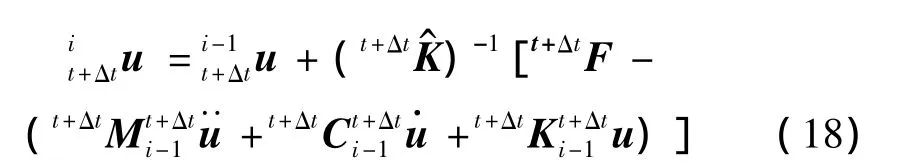
检查收敛性，若收敛，即得到本时间步最终的位移增量t+Δtu，进而求得 t+Δt时刻的位移、速度以及加速度。

4 算例

算例1 为了说明结点6自由度模型分析输电线的正确性，编制程序，分析了文献［19］中的一根输电线。该输电线为一小垂跨比输电线，输电线质量0.821 7 kg/m，刚度为 EI为 11.07 Nm2，输电线的轴力为15 860 N，输电线长为13.385 m。表1表示文献［19］中所列出 Irvine 方法［5］、Desai方法［12］、试验值与本文理论分析该输电线的模态分析结果比较。结果表明，对于上该输电线，由于垂跨比较小，上述4种理论均与试验吻合较好。由于曲梁理论推导没有小垂跨比假设，因此，结点6自由度模型可以适用于更广泛的输电线分析。

表1 不同理论模型分析频率(Hz)Tab.1 Mode analysis with different compute model(Hz)

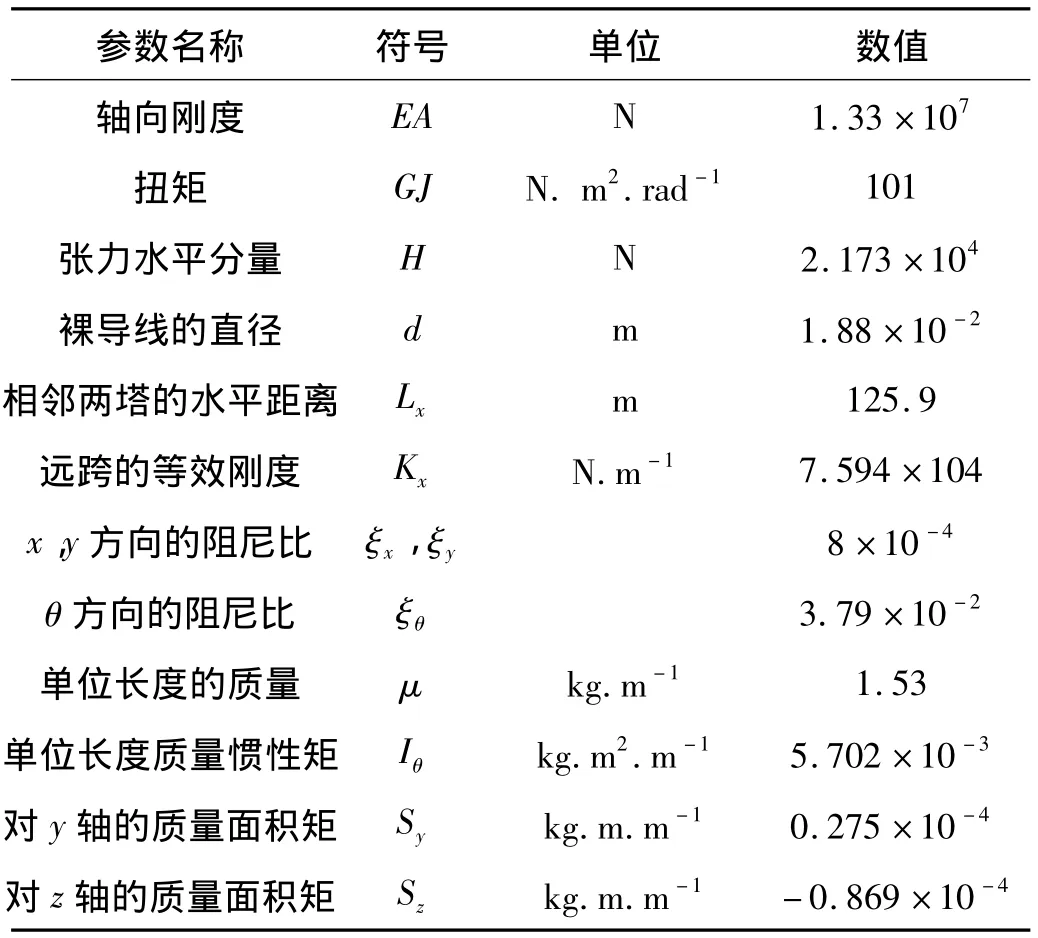
表2 单根导线的物理参数Tab.2 Physical parameters of single conductor

算例2 上述算例表示结点6自由度模型计算线性模态是正确的，为了考察其非线性舞动特性，这里采用6自由度模型计算文献［12］的一个经典覆冰导线舞动算例。算例物理参数如表2，气动参数可以参考原文献。该导线是覆冰形状为D型截面，有野外舞动观测的数据，现有众多的数值分析文献大都利用该野外观测数据进行验证，遗憾的是，野外原始数据中缺少了两个关键的截面参数Sy、Sz。文献［12］假设了这两个参数，分析结果与野外数据吻合较好，本文取值按表2。利用结点6自由度单元进行该导线的舞动分析，编制计算程序，采用Newmark-β法解动力方程。得到初始攻角为100、风速4.1 m/s时的导线舞动轨迹，如图2～图4所示。

图2 本文计算结果与文献［12］比较Fig.2 Comparison between reference［12］and this paper

将计算结果与文献［12］中的计算结果［图2(a)］进行对比。［图2(a)］的中心点位置为(0.04，1.38)，图2b)的中心点位置为(0.003，0.005)，这是由于本文图示位置是基于平衡位置;计算y方向的最大振幅为0.79 m，在侧向的最大振幅为0.02 m，幅值平面的夹角为 0.8°，计算结果有效。

图3～图4分别为输电线舞动时中点的竖向位移及扭转位移时程曲线，计算初值取竖向振幅为0.001m，计算步长取0.001 s，大约在2 500 s振动趋于稳定。由于扭转刚度较低，该导线产生较大的扭转角，属于扭转大变形。传统的3自由度舞动分析模型在处理扭转角时没有考虑抗弯刚度的影响，并且扭转变形是基于小变形、线弹性假设推导的。从图4可以看出，上述假设并不成立，需要考虑扭转非线性的影响。由于本例在4.1m/s风速下发生的是频率比1∶1∶1(侧向频率:竖向频率:扭转频率)的共振，因此，在舞动发生时，竖向振动、侧向振动以及扭转角振动的锁定频率是一致的，振幅是相互耦联的。从时程分析计算可知，发生舞动与初始条件无关，是一种自激振动。

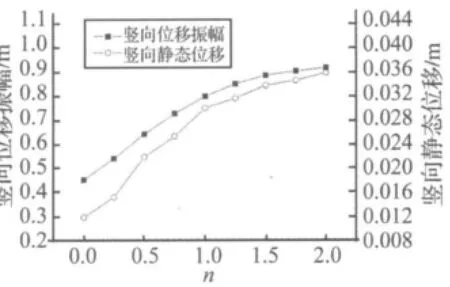
图5 不同抗弯刚度对舞动竖向位移的影响Fig.5 Vertical galloping displacement of different bend stiffness

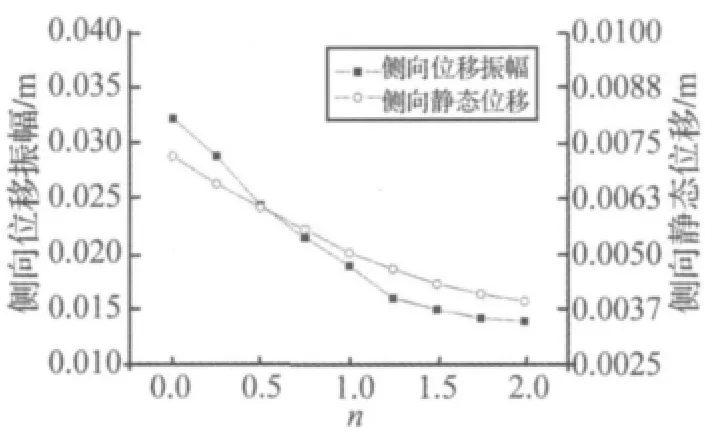
图6 不同抗弯刚度对舞动侧向位移的影响Fig.6 Lateral galloping displacement of different bend stiffness

图7 不同抗弯刚度对舞动竖向位移的影响Fig.7 Torsional galloping angle of different bend stiffness

图5～图7表示假设该导线不同的截面抗弯刚度采用结点6自由度模型分析输电线舞动动态振幅和静态偏移。导线参数和气动力参数仍然如表2，只是原文献缺乏导线的抗弯刚度数据，这里根据原文献的截面形式，假使导线截面均匀分布，确定导线横截面上各个方向的抗弯刚度EI为294 N·m2，图中横坐标n表示EI的倍数。实心点曲线表示舞动的动态振幅，空心点曲线表示舞动的静态偏移。图5表明，随抗弯刚度增加，竖向舞动振幅及静态偏移均增大;图6表明，随抗弯刚度增加，侧向舞动振幅及静态偏移均减小;图7表明，随抗弯刚度增加，竖向舞动振幅减小，但静态偏移变化不大。可见，由于覆冰输电线抗弯刚度与抗扭刚度属同一个数量级，其对输电线舞动的扭转有较大影响，又因为根据式(13)所推导的准定常气动力产生了与平动相关的耦联项，因此对输电线舞动的平动振幅也有较大影响。

5 结论

传统的输电线3自由度舞动分析模型无法考虑扭转与平动的耦合作用及扭转运动的非线性。利用3结点6自由度曲梁理论求解输电线的舞动问题可以合理地反映上述关系。基于6自由度曲梁的应变—位移关系，建立了结点包含具有3个平动自由度和3个转角自由度的输电线舞动分析有限元模型。考虑覆冰导线所受空气动力的非线性和导线大幅运动的几何非线性，利用虚功原理建立基于更新Lagrange格式的覆冰导线非线性运动方程。采用 Newmark时间积分和Newton-Raphson非线性迭代法求解有限元方程。算例分析表明，输电线的抗弯截面模量对输电线的平动和扭转有较大的影响。现有的舞动机理如垂直运动激发理论、扭转激发理论以及惯性偏心激发理论实际上是基于单自由度、2自由度或3自由度的理论，是6自由度耦合运动的特例或近似。

［1］郭应龙，李国兴，尤传永.输电线路舞动［M］.北京:中国电力出版社，2003.

［2］ Den Hartog J P.Mechanical vibration［M］.New York:Mcgraw-Hill，1956.

［3］Nigol O，Buchan P G.Conductor galloping partⅠ-den hartogmechanism ［J］. IEEE Transactions on Power Apparatus and System，1981，100(2):699-707.

［4］Nigol O，Buchan P G.Conductor galloping partⅡ-torsional mechanism［J］.IEEE Transactions on Power Apparatus and System，1981，100(2):708-720.

［5］Haaker T I，Vanoudheusden B W.One-degree-of-freedom rotational galloping understrong wind conditions［J］.International Journal of Non-linear Mechanics，1997，32(5):803-814.

［6］ Byun G S，Egbert R I.2-degree-of-freedom analysis of power-line galloping by describing function methods［J］.Electric Power Systems Research，1991，21(3):187-193.

［7］Yu P，Shah A H，Popplewell N.Inertially coupled galloping of iced conductors［J］.Journal of Applied Mechanicstransactions of the ASME，1992，59(1):140-145.

［8］ Jones K F.Coupled vertical and horizontal galloping［J］.Journal of Engineering Mechanics，1992，118(1):92-107.

［9］Yu P，Desai Y M，Shah A H.3-degree-of-freedom model for galloping-1. formulation［J］. Journal of Engineering Mechanics-ASCE，1993，119(12):2404-2425.

［10］Yu P，Desai Y M，Popplewell N.3-degree-of-freedom model for galloping-2. solutions［J］. JournalofEngineering Mechanics-ASCE，1993，119(12):2426-2448.

［11］ Yu P，Popplewell N，Shah A H.Instability trends of inertially coupled galloping:periodic vibrations［J］.Journal of Sound and Vibration，1995，183(4):679-691.

［12］ Desai Y M，Yu P，Popplewell N，et al.Finite element modeling of transmission line galloping［J］.Computers and Structures，1995，57(3):407-420.

［13］ Desai Y M，Yu P，Shan A H，et al.Perturbation-based finite element analyses of transmission lines galloping［J］.Journal of Sound and Vibration，1996，191(4):469-489.

［14］樊社新，何国金，廖小平，等.结冰导线舞动机制分析［J］.中国电机工程学报，2006(14):131-133.

［15］范钦珊，官 飞，赵坤民，等.覆冰导线舞动的机理分析及动态模拟［J］.清华大学学报(自然科学版)，1995(2):34-40.

［16］胡 杰，郭应龙，恽俐丽.三分裂输电导线舞动的有限元分析与计算［J］.水利电力机械，1996(4):9-12.

［17］刘小会，严 波，张宏雁，等.覆冰导线舞动非线性数值模拟方法［J］.应用数学和力学，2009，30(4)，:457-468.

［18］Wang J W，Lilien J L.Overhead electrical transmission line galloping-a full multi-span 3-DOF model，some application and design recommendations［J］.IEEE Transaction on Power Delivery，1998，13(3):909-915.

［19］Irvine H M，Cable structures［M］.New York:MIT Press，1981.

［20］ Mc Connell K G，Chang C N.A study of the axial-torsional coupling effect on a sagged transmission line［J］.Experimental Mechanics，1986，26(4):324-329.

［21］Angelo L，Zulli D ，Piccardo G.Analytical and numerical approaches tononlineargallopingofinternally resonant suspended cables［J］.Journal of Sound and Vibration，2008，(315):375-393.

［22］Angelo L，Zulli D ，Piccardo G.On the effect of twist angle on nonlinear galloping of suspended cables［J］.Computers and Structures，2009，87(15-16):1-12.

［23］Zhu Z H，Meguid S A.Vibration analysis of a new curved beam element［J］.Journal of Sound and Vibration，2008，309(1-2):86-95.