环境条件影响下悬索桥模态频率变异性的定量评价
2011-02-13丁幼亮李爱群
邓 扬,丁幼亮,李爱群
(东南大学 混凝土及预应力混凝土结构教育部重点实验室,南京 210096)
对于运营状态下的大跨桥梁结构而言,在环境温度和运营载荷等环境条件的变化影响下,结构实测模态频率会在一个较宽的范围内波动,这种波动将淹没或掩盖结构因局部损伤所造成的结构模态频率的真正改变,从而对结构的损伤诊断和状态评估产生不利的影响[1,2]。国内外的学者对此进行了大量的研究[1-6],目前大部分的学者认为温度是影响桥梁结构模态频率变化的最主要因素[3],除此之外,车辆荷载以及风速对大跨桥梁模态参数的影响甚微[4,5]。
但目前还没有学者同时定量地分析了温度、交通荷载及风速所产生的频率识别的变异性,大部分的研究都仅限于一种环境因素的影响或仅得到了环境因素对频率识别的定性影响趋势。另一方面,最重要的是大部分的研究都没有考虑识别方法所引起的频率识别结果的随机误差,例如文献5分析了环境因素对Ting Kau Bridge模态频率的影响,前十阶频率识别结果的相对变化范围为3.22%到15.07%,在消除温度所引起的变化后,频率的相对变化范围减小至1.61%到7.87%,在此基础上的分析表明频率和风速之间的相关性十分微弱,风速所引起的模态频率的变化不明显,这表明在消除环境因素的影响之后,模态频率的相对变化仍很可观,而导致这种结果的原因就只能是频率识别方法所产生的随机误差,到目前为止还没有学者对此进行讨论。
本文将基于长期监测数据量化评价温度、风速、交通荷载及识别方法所引起的润扬大桥悬索桥结构模态频率的变异性,首先采用基于输出的频域识别方法得到模态频率测试值,采用多样本平均技术减小识别算法引起的随机误差,其次基于频率-温度相关性模型消除温度对频率的影响,再在小风速的情况下建立频率和加速度响应均方根的相关性模型以评价交通荷载对频率的影响,在此基础上,分析了模态频率和风速的相关性,得到了风速对频率变化影响的量化评价。
1 模态频率的现场实测
本文以润扬大桥悬索桥为研究对象,其结构健康监测系统共安装了29个加速度传感器,分别布置在主梁八分点截面处,同时,在主梁的北端、北侧1/8截面、北侧1/4截面和南端共安装了27个温度传感器,并在主跨跨中和南塔塔顶分别安装了风速风向仪,加速度传感器的采样频率为20 Hz,温度和风监测的采样频率则均为1 Hz[7,8]。为了得到准确和可信的结构模态频率,对结构健康监测系统在2006年1月至10月所采集的长期监测数据进行了分析,在这段时间内,大桥经历了一年四季的温度变化、台风和强北风的来袭以及交通流量的逐渐增加,因此,模态频率的识别结果中包含了丰富的环境条件的影响,具有普适性和代表性。本文采用峰值法识别润扬悬索桥结构的模态频率,其基本思想是:结构动力响应的频率响应函数在结构固有频率处达到极值,在仅有输出的环境振动测试中,频率响应函数可以被输出的自功率谱所取代,取自功率谱密度图上的峰值即可以确定结构的模态频率。但频域峰值法存在着截尾误差和频率分辨率有限的缺陷,为了克服这些缺陷,本文采用窗口迭代曲线拟合方法(Iterative Windowed Curve-fitting Method,简称 IWCM)改进了频率识别结果,IWCM的详细介绍见文献[9]。
图1给出了主梁截面5的竖向典型加速度响应时程,从中可以看出,悬索桥的动力响应在一定时间尺度内是非平稳的。图2给出了第5阶竖弯模态频率一天的测试结果,可以看出温度变化对频率影响是长期的和趋势性的,而伴随的频率的瞬时颤动变化则是随机的,并且变化幅度也是可观的。这种随机变化是由环境激励的非平稳性所造成的,本文认为算法所引起的模态频率识别随机误差是不能忽视的,下面本文将基于长期监测数据对润扬悬索桥的模态频率识别变异性进行详细的讨论。

图1 主梁截面5的竖向加速度时程Fig.1 Vertical acceleration time histories of the Sec.5

图2 第5阶竖弯模态的频率实测序列Fig.2 Measured frequency sequences of the 5th symmetric vertical mode
2 温度导致的模态频率变异性
2.1 频率识别的随机误差分析
去除显著异常的测试数据之后,得到了2006年1月至10月215天的有效监测数据,在此基础上以10-min为时间区间识别得到了悬索桥前6阶竖弯振型的模态频率,分别为1阶对称、2阶反对称、3阶反对称、4阶对称、4阶反对称和5阶对称。每阶模态频率得到了30960(144×215)个实测样本。图3(a)~图3(d)分别给出了第2、4、5和6阶模态频率和温度之间的相关散点图,需要说明的是图中的温度值采用的是全桥所有温度传感器测试值的平均值。从图3可以看出随着温度的增大,各阶模态频率都呈现出减小的变化趋势,但频率与温度的相关性散点分布比较离散,呈现明显的带状分布特征,即同一温度值对应的实测模态频率可以在一个较宽的范围内波动,这种频率的波动应该被认为是由于识别算法所不能处理的激励非平稳性所引起的随机误差,显然,由图3难以有效地建立悬索桥实测模态频率与温度的统计模型。
为了有效地消除这种随机误差,本文采用多样本平均方法来分析模态频率和温度的相关性,即以每天144个测试样本的日平均值作为频率的测试值,图4给出了模态频率日平均值与温度日平均值之间的相关性分析结果。从图4可以看出通过取多样本的日平均值后,由于高阶振型的频率受温度的影响较低阶振型大,因此低阶模态频率与温度的季节相关性较差,散点图仍然比较离散,而高阶模态频率与温度之间呈现十分明显的季节相关性,散点图分布较图3更为集中。


表1进一步给出了模态频率10-min识别值和1-day平均值的统计信息,从表1可以发现模态频率相对变化的最大值和平均值分别从3.013%和2.633%减小到2.168%和1.268%。这说明多样本平均方法消除了悬索桥温度日变化对模态频率的影响,而保留了季节温度变化的影响,同时也可以有效地减小由识别方法的局限性所造成的模态频率识别值的随机误差。
2.2 频率-温度相关性模型
为了定量地评价温度对模态频率的影响,前提是建立频率-温度的相关性数学模型,分析表明5次以上的多项式模型误差趋于稳定,因此,采用6次多项式模型建立模态频率f与温度T的季节相关性回归公式[10]:

式中,T为温度日平均值;f为悬索桥模态频率的日平均值;pi(i=1~7)为回归模型的系数。基于悬索桥2006年的215个实测模态频率和温度日平均监测样本,采用最小二乘法拟合得到了频率-温度的季节相关性模型。
为了考察6次多项式模型对季节相关性的拟合效果,图5给出了第2阶和第6阶模态频率实测值和预测值的对比结果,图中实线为频率实测值,虚线为基于回归模型的频率计算值。可以看出频率实测值与计算值曲线比较吻合,说明采用6次多项式模型的拟合效果良好,能够很好地刻画频率和温度的季节相关性,因此就可以采用本文提出的多项式回归模型实现对温度引起的频率识别变异性的量化评价。表2给出了当温度分别为0℃和40℃时,根据回归模型计算得到的悬索桥前6阶模态频率,从中可以看出,温度对高阶频率的影响较大,而对低阶频率影响较小,第5阶模态频率的相对变化最大,为1.975%,第1阶模态频率的相对变化最小,仅为0.397%。
2.3 环境温度归一化的模态频率
为了后续研究悬索桥模态频率与交通荷载、风速的相关性,前提是将温度对频率的影响从频率的实测值中消除掉,即得到环境温度归一化的模态频率。统计分析表明,本文选取的215天内,风和交通荷载的日平均值变化很小,与温度的日平均值变化相比较可以忽略。因此可以认为本文2.2节建立的模态频率-温度的日平均相关模型不包含风和交通荷载的影响,故采用2.2节的日平均相关性模型去消除温度对频率的影响是合理的。

表1 模态频率实测结果的统计特性Tab.1 Statistics of measured modal frequencies

表2 温度所引起的模态频率识别的变异性Tab.2 Variations of frequency induced by temperature

图5 模态频率测试值和预测值的对比结果Fig.5 Comparisons of the measured and predicted results of frequencies
具体方法是取参考温度值为20℃,将参考温度值代入回归模型,得到每一阶频率的参考频率fr,同样地将实测温度值代入回归模型,得到模态频率的计算值ft,则环境温度归一化的模态频率可以表示为:

式中,f为归一化后的频率;fm为实测频率。这里需要说明的是,模态频率的10-min测试值和1-day平均值均采用3.2节的季节相关性模型进行温度归一化,图6和图7分别给出了第6阶模态频率10-min和1-day平均的实测值和温度归一化值,图7中实线表示频率实测值,虚线表示归一化值。对比图6和图7可以看出,对于模态频率10-min和1-day平均的温度归一化值而言,温度对频率的趋势性影响都被有效地消除了,但是频率的10-min归一化值仍然保有较宽的变化范围,而频率1-day平均的归一化值的变化范围则较小。


表3进一步给出了温度归一化后悬索桥前6阶模态频率值的统计特性。与表1给出的频率实测结果对比可以发现:(1)模态频率10-min实测值的相对变化的最大值和平均值分别仅从3.013%和2.633%减小到2.506%和2.027%,减小幅度很小,这说明非平稳激励对频率识别结果的影响仍较为显著,识别方法的缺陷所带来的模态频率随机误差仍然较为明显;(2)模态频率1-day平均值的相对变化的最大值和平均值分别从2.168%和 1.268%减小到 0.582% 和 0.413%,这说明不仅温度对频率的影响被有效地消除了,同时非平稳激励所引起的频率识别随机误差也被有效地降低了。

表3 环境温度归一化的模态频率的统计特性Tab.3 Statistics of normalized modal frequencies
3 交通荷载和风导致的模态频率变异性
3.1 频率-交通荷载相关性模型
本节将研究温度归一化模态频率和交通荷载的相关性,采用悬索桥主梁竖向加速度响应的均方根(root mean square,RMS)作为交通荷载的表征值[4]。首先挑选出小风速状态(10-min平均风速小于2m/s)的加速度响应数据,认为此时能对模态频率产生影响的环境因素就只有交通荷载了,其次对挑选出来的加速度响应进行低通滤波,截止频率为3Hz,通过滤波得到仅含有结构动力响应的加速度数据,最后分析温度归一化的10-min模态频率和10-min加速度响应均方根的相关性。图8给出了第1、3、4和6阶模态频率和加速度均方根的相关性散点图,可以看出图中频率-RMS的散点图分布十分离散,模态频率和交通荷载的相关性较弱。进一步采用线性回归分析建立温度归一化频率f和RMS的相关性模型,模型表达式为:
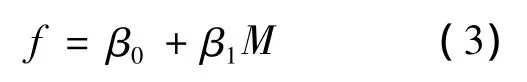
式中,M为 RMS的值;β0和 β1为回归系数。回归系数可通过最小二乘的方法得到:
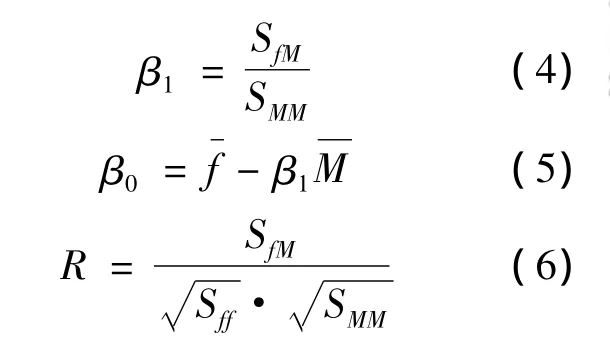
式中,SfM为频率与RMS的协方差;SMM为RMS的方差;Sff为频率的方差;和分别为RMS和频率的均值;R为频率和RMS的相关系数。表4给出了频率和交通荷载的线性回归模型以及交通荷载所导致的模态频率的变化。从表4可以看到,所有线性回归模型的斜率都为负值,这表明随着交通荷载的增强,悬索桥模态频率有轻微的减小变化趋势。另外,表4给出了RMS分别为0 cm/s2和3 cm/s2时,根据回归模型计算得到的悬索桥前6阶模态频率,其中第2阶模态频率的相对变化最大,为0.262%,这说明交通荷载对频率变化的影响甚微。
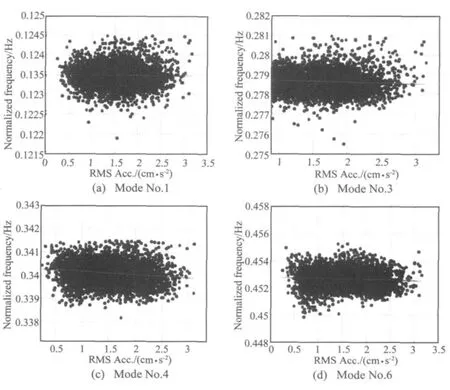
图8 温度归一化的模态频率和加速度响应均方根的相关性Fig.8 Correlation between normalized modal frequency and RMS of the acceleration responses

表4 频率-交通荷载的线性回归模型和交通荷载导致的模态频率变异性Tab.4 linear regression models of frequency-traffic and variations induced by traffic loadings

表5 频率-风速的线性回归模型和风速导致的模态频率变异性Tab.5 linear regression models of frequency-traffic and variations induced by traffic loadings
3.2 频率-风速相关性模型
本节将在上文的基础上消除交通荷载对模态频率的影响,即得到的RMS归一化的频率,此时频率的变化就仅受风速这一种环境因素的影响,在此基础上再分析频率和风速的相关性。采用类似3.3节的方法,将频率归一化至某一参考RMS值:


图9 模态频率和风速的相关性Fig.9 Correlation between normalized modal frequency and wind speed
式中,f为RMS归一化的频率;fm为温度归一化的频率;ft为将RMS实测值代入3.1节频率-RMS回归模型的频率计算值;fr为参考频率,其计算过程为设定RMS参考值为1 cm/s2,代入回归模型计算得到。
在此基础上,图9给出了第1、3、5和6阶RMS归一化模态频率和风速的相关性散点图,可以看出图中频率-风速的散点图分布十分离散,模态频率和风速的相关性较弱。采用与3.1节一样的线性回归模型对频率-风速相关性进行建模,表5给出了频率和风速的回归模型以及风速引起的模态频率的变化。从表5可以看到,线性回归模型的斜率都为正值,这表明随着风速的增强,悬索桥模态频率有轻微的增大趋势。同时,表5给出了风速分别为0 m/s和20 m/s时,根据回归模型计算得到的悬索桥前6阶模态频率,其中第1阶模态频率的相对变化最大,为0.215%,这说明风速对频率变化的影响也很微弱。
4 结论
本文定量地分析了频率识别方法、环境温度、交通荷载及风速这四个因素对润扬大桥悬索桥模态频率识别的影响程度,得到了以下结论:
(1)采用多样本平均方法可以有效地减小由识别方法的局限性所造成的频率识别值的随机误差。通过多样本使得悬索桥的模态频率相对变化的最大值和平均值分别从3.013%和2.633%减小到了2.168%和1.268%。
(2)环境温度是对频率变化影响最大的因素。随着各阶频率都表现出随温度升高而减小的变化趋势。采用6次多项式模型有效地消除了温度对频率的影响,分析表明由温度引起的频率相对变化的最大值和平均值分别为1.975%和1.175%。
(3)交通荷载对频率的变化影响甚微,两者相关性较弱。随着交通荷载的增强,悬索桥模态频率有轻微的减小趋势,采用线性回归方法建立了温度-RMS相关性模型,分析发现由交通荷载引起的频率相对变化的最大值和平均值分别为0.262%和0.104%。
(4)与交通荷载类似,风速对频率变化的影响也很小,两者相关性也较弱。同样采用线性回归方法建立了温度-风速相关性模型,分析发现由风速引起的频率相对变化的最大值和平均值分别为0.215%和0.163%。
(5)分析表明,激励非平稳性引起的频率识别值的随机性非常明显。本文2.1节采用取频率日平均值的方法可以较好地消除这种随机性,但对于较小时间尺度(如10-min)的频率值的随机性却没有合适的处理办法,因此在本文3.1和3.2节消除风和交通荷载影响之后的模态频率识别值中仍然包含了识别过程所产生的随机性,这也是图9的频率分布仍十分离散的原因。
(6)由于问题的复杂性,很难通过理论分析得到环境条件对模态频率影响规律的先验的合理描述,因此本文通过对结构健康监测系统海量监测数据的分析,采用简单回归模型从实测的角度研究了温度、风和交通荷载对模态频率的影响,从一定程度上揭示了环境条件对悬索桥模态频率的影响规律。本文的研究是初步的,在此基础上进一步开展深入的研究工作是必要的。
[1] Ni Y Q,Hua X G.Fan K Q,et al.Correlating modal properties with temperature using long-term monitoring data and support vector machine technique[J].Engineering Structures,2005,27(12):1762-1773.
[2] Ding Y L,Li A Q,Liu T.Environmental variability study on the measured responses of runyang cable-stayed bridge using wavelet packet analysis[J].Science in China Series E:Technological Sciences,2008,51(5):517-528.
[3]Cornwell P,Farrar C R,Doebling S W,et al.Environmental variability of modal properties[J].Experimental Techniques,1999,23(6):45-48.
[4]Zhang Q W,Fan L C,Yuan W C.Traffic-induced variability in dynamic properties of cable-stayed bridge[J].Earthquake Engineering and Structural Dynamics,2002,31(11):2015-2021.
[5]Ni Y Q,Ko J M,Hua X G,et al.Variability of measured modal frequencies of a cable-stayed bridge under different wind conditions[J].Smart Structures and Systems,2007,3(3):341-356.
[6]李顺龙,李 惠,欧进萍,等.考虑温度和风速影响的桥梁结构模态参数分析[J].土木工程学报,2009,42(4):100-106.
[7]李爱群,缪长青,李兆霞,等.润扬长江公路大桥结构健康监测系统研究[J].东南大学学报,2003,33(5):544-548.
[8] Li A Q,Miao C Q.Design and study on the structural health monitoring system for the Runyang Yangtse River bridge[C]//Proceedings of the 2nd International Conference on Structural Health Monitoring of Intelligent Infrastructure.Shenzhen,China,2005.
[9]Macdonald J H G.Identification of the dynamic behaviour of a cable-stayed bridge from full-scale testing during and after construction[D].University of Bristol,2000.
[10]孙 君,李爱群,丁幼亮,等.润扬大桥悬索桥模态频率-温度的季节相关性研究及其应用[J].工程力学,2009,26(9):50-55.