快速评估风电场50年一遇最大风速的算法
2016-03-04盖峰邹长宁袁飞
文 | 盖峰,邹长宁,袁飞
快速评估风电场50年一遇最大风速的算法
文 | 盖峰,邹长宁,袁飞
轮毂高度处的50年一遇最大风速是风电机组选型的重要指标,也是评估风电机组极限载荷的重要依据。在《全国风能资源评价技术规定》中给出了利用气象站数据计算50年一遇最大风速的计算公式,其中要求气象站连续15年以上最大风速样本序列。
目前,气象站统计数据普遍存在着气象站统计数据短缺、迁站、受周边地形地貌影响的问题;在我国的风电场建设过程中,又存在着气象站距风电场较远、地形地貌相差较大、测风数据的相关性差的问题。为此,在实际工作中,业内普遍采用的方法有5倍平均风速法、WAsP Engineering分析法、5日风暴法、独立风暴法等。
但在以上方法中,5倍平均风速法与WAsP Engineering分析法基于欧洲经验,相关推理不够明确;其他方法对于理论的要求较高,难以被多数从业者所掌握。因此,本文将从本质上探讨风电场50年一遇最大风速的概率算法,并给出一种针对理想威布尔分布的快速计算方法,为计算风电场50年一遇最大风速,为风电机组选型以及极限载荷计算提供参考依据。
理论基础
一、重现期概念
在水文和气象上,“N年一遇”的科学表述“重现期”,50年一遇最大风速的意义就是每出现一次10分钟风速超过该风速的平均所需时间间隔为50年。
基于以上定义,理论上50年一遇最大风速出现的概率应为:
二、威布尔分布累计概率
在通常情况下,风速分布服从威布尔分布,所以根据威布尔分布的形状参数k值和尺度参数A值(或C值),可以计算出风速超过高于任意风速V所出现的累计概率,即:
三、 50年一遇最大风速计算
根据50年一遇最大风速的定义,可以得到在风速服从标准威布尔分布的情况下,50年一遇最大风速V50与代表年平均风速的倍数n50和威布尔分布k值之间存在如下关系:
将式(5)左右两侧分别取两次对数,可以得到:
5倍平均风速法验证
根据式(6),可以计算得到不同k值对应的50年一遇最大风速V50与代表年平均风速的倍数n50,如图1所示。
根据以上计算结果,在威布尔分布k值约为1.8336时,n50约等于5,随着k值逐渐增大,n50逐渐减小,即在k值大于1.8336时,n50取5计算得到的50年一遇最大风速V50偏大,在安全性评估方面较为保守。
同时,根据欧洲经验,在k值为1.8-2.3范围内时,50年一遇最大风速V50与代表年平均风速的比值可取5,与以上分析结果一致,且较为保守。
基于标准威布尔分布的N倍平均风速法
通过对式(4)进行变形,可以得到重现期T与n和k之间的关系如下:
在威布尔分布k值为2(即标准瑞利分布)时,n取5,可以得到重现期T为44458年,即在风速服从标准瑞利分布的情况下,采用5倍平均风速法求得的风速重现期远大于50年,因而对50年一遇最大风速的计算过大,机组选型较为保守。
而在某些威布尔分布k值过小的地区,采用5倍平均风速法则又会对50年一遇最大风速计算过小,机组选型又将倾向于激进。
根据以上分析,可以发现采用5倍平均风速法计算50年一遇最大风速较为笼统,容易出现结果偏大或偏小的问题,对此,本文提出了一种基于标准威布尔分布的N倍平均风速法。
5倍法与N倍法计算结果对比
分别采用5倍平均风速法与N倍平均风速法,对不同风速分布下的极限风速进行计算,可以得到:
从表1可以看出,在威布尔分布k值约小于1.8336时,采用5倍平均风速法计算得到的50年一遇最大风速小于N倍平均风速法的结果;而在k值大于1.8336时,采用5倍平均风速法计算得到的50年一遇最大风速大于N倍平均风速法的结果。
对于k值取1.5与3.5的两种特例,笔者曾在两个海外项目中遇到过此类情况,对于威布尔分布k值约为1.5的某中纬度风电场,平均风速约为7.5m/s,但根据现场反馈出现大风的频率非常高,且风速很大;而对于威布尔分布k值超过3的某赤道附近风电场,不仅在实际测风过程中20m/s以上风速的出现频率极低,而且根据现场走访,历史上也未出现过台风等极端气候。这两个实例都在一定程度上印证了以上分析的合理性。
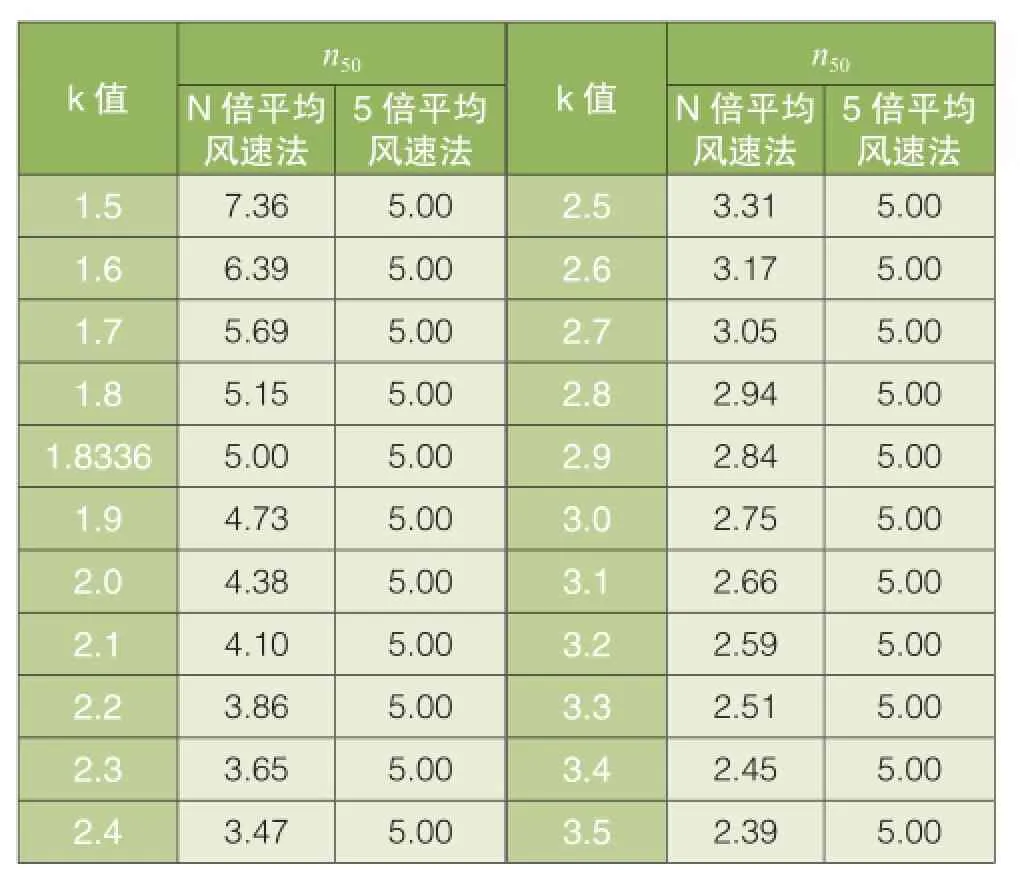
表1 n50随k值变化趋势
结论
综上所述,可以得到以下结论:
1.基于欧洲经验的5倍平均风速法与理论计算结果相吻合,在威布尔分布k值为1.8-2.3的范围内适用。
2.在风速分布服从标准威布尔分布的情况下,采用5倍平均风速法的计算结果会随着k值增大/减小而使机组选型倾向于保守/激进,且在k值为2时,极限风速重现期达到44458年。
3.在风速分布服从标准威布尔分布的情况下,采用基于标准威布尔分布的N倍平均风速法,50年一遇最大风速计算结果随威布尔分布k值增大/减小而减小/增大,更为合理。
(作者单位:国电联合动力技术有限公司)
