金属橡胶材料恢复力的三维模型

刘远方，白鸿柏，李冬伟，王尤颜，陶 帅

(军械工程学院，石家庄 050003)

金属橡胶材料是一种由细金属丝堆叠冲压制成的多孔非线性弹性阻尼材料［1，2］，内部作用机理十分复杂，关于其恢复力的认识和表征，一直以来缺乏严密准确的模型。现有非线性弹性阻尼材料力学研究，在国外比较有代表性的是:双线性恢复力模型［3］、一阶线性微分方程模型［4］和迹法模型［5］等;在国内比较有代表性的是，上海交大博士龚宪生［6］认为，钢丝绳的恢复力具有非线性迟滞特性(其特性与金属橡胶基本相同)，其恢复力是动刚度和阻尼的函数，而其动刚度和阻尼又是振幅和频率的非线性函数。文献［7］对当前非线性弹性阻尼元件恢复力的建模和参数辨识给予了概括地介绍和整理，事实上现有恢复力模型对材料恢复力进行定性分析有一定成效，但是由于材料刚度和阻尼非线性性质的复杂和作用机理的差异，定量研究的模型多数存在模型过于抽象和参数辨识复杂的问题，对于具体的科学实践来说缺乏针对性和操作性。

本文以Matlab软件为平台，以大量试验数据分析为基础，对一组离散谐波激励条件下获得的位移和恢复力数据进行整合处理，通过合理的插值拟合，结合金属橡胶实际作用机理，设计拟合方法和模型结构形式，分别应用曲线和曲面拟合的最小二乘法，拟合恢复力关于位移和速度的二元解析方程。摒弃了现有模型在建立和应用时粗糙的线性简化处理方法，解决了恢复力表征方法依赖谐波激励振幅和频率的弊端，实现了对金属橡胶等非线性弹性阻尼材料恢复力解析表达的突破。

1 恢复力三维模型的一般形式

在非线性振动的微分方程中，惯性力、阻尼力或弹性力并不分别与加速度、速度及位移的一次方成正比［8］，文献［9］也提到了非线性刚度和非线性阻尼的有关特征，在获得试验结果之前，概括性地认为金属橡胶恢复力由对应状态的位移和速度所决定:

其中z为恢复力;x为位移;y为速度;f为函数关系。

不同于现有二维模型的恢复力只以位移为变量，也不同于以谐波振幅和频率为自变量的伪三维恢复力模型，本模型中恢复力表示为位移和速度的二元函数，具体模型结构将在数据处理之后，根据数据特征给出具体形式。

众所周知，速度是位移的导数，一般不能认为位移和速度是两个独立变量，但是因研究问题的具体情况和空间形式等原因，位移和速度在某些场合也可以作为两个独立变量来处理。如图1所示，以位移和速度为变量的坐标系，当外界激励是不同振幅和频率的谐波时，位移和速度在每个闭合曲线上存在唯一的确定性关系，但是因为曲线的不同，这个确定的关系也在改变，所以在整个定义域上，位移和速度具有不确定关系，可以作为三维恢复力模型中恢复力表达式的两个独立变量。

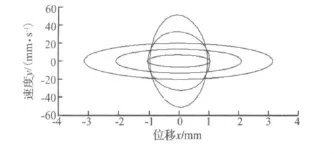
图1 不同振幅和频率谐波激励下的位移和速度关系Fig.1 The displacement-speed relation under the harmonic excitation of different amplitude and frequency

2 恢复力三维模型结构分析和参数辨识

模型的建立以足够的试验数据分析为基础，通过数据的处理和材料实际力学作用机理的分析，得到模型的合理结构形式。

2.1 数据采集

以电液伺服式材料试验机为依托，选取某种工艺的中空圆柱形金属橡胶试件，按照边缘固支的悬臂梁方式夹持，中心孔处施加垂直于圆形端面的位移谐波激励，试件产生剪切和弯曲变形(注:本模型)。以1 000 Hz的采样频率对试件的位移和恢复力进行数据采样，储存为一组txt格式的文本文件。

根据试件的使用场合(即:工作的位移和速度限定范围)，在保证各位移和速度曲线在投影面分布均匀而充足的前提下，为了便于理论研究，设计如表1所示多种谐波激励试验，有“√”标记的情况需要进行试验。

2.2 数据的预处理

由于受到试验中传感器精度、设备误差、安装误差和文献［10］所提到的干摩擦运动的跃动现象等因素的影响，原始数据不可避免地会出现对称性和光滑度不理想的问题，必须对数据进行去直流分量和平滑处理。首先，对各数据去直流分量，以MATLAB软件为平台依次导入位移和恢复力的试验数据，通过以下命令实现去直流分量处理:x=x-mean(x)，z=z-mean(z);然后，对位移和恢复力数据进行傅里叶变换处理后重构，通过重构后的位移解析式求导获得速度数据以及实现恢复力的平滑处理(因为是位移控制，所以位移数据曲线处理前后光滑度变化不大)，如图2所示，图2(a)是恢复力处理前图示，图2(b)为处理后图示，可以明显看出处理前后曲线光滑度的差异。

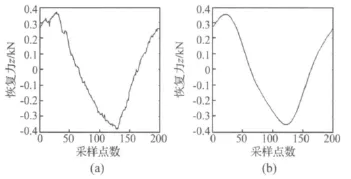
图2 数据预处理前、后的恢复力Fig.2 The restoring force before processed and after processed

表1 试验设计A为振幅(mm)，ω为频率(Hz))Tab.1 Experimental design(A represent amplitude(mm)，ω represent frequency(Hz))

2.3 数据的插值处理

虽然各曲线在位移——速度投影面上分布基本均匀，但是很难保证所有预处理后的数据点关于投影面均匀分布，如果直接进行空间曲面的最小二乘拟合，无法保证拟合精度，所以必须进行插值处理，得到关于投影面均匀的数据点。MATLAB软件无法直接对一组向量进行插值，只有当数据具有如下特征时才可以:变量x和y都是一维向量，各自元素大小分别顺序排列，向量 x，y通过命令［x，y］=meshgrid(x，y)变成矩阵，矩阵x的一个元素xi和矩阵y的一个元素yj刚好对应矩阵z的一个元素zij，只有在这种情况下才可以进行二维插值(一维插值针对曲线，二维插值针对曲面)，所以必须对数据进行插值前的整合，使之具有MATLAB软件可识别的特征。本文的处理方法是，将预处理后的数据根据需要的投影面分辨率(10×10网格，根据情况自行设计)对所有数据进行压缩整合，即在需要的投影面范围x:(-a，a)，y:(-b，b)内，将所有数据按照 10 ×10网格分割处理，把每一网格的中心坐标分别赋值给矩阵x和y对应的元素，把网格内所有预处理后数据点的恢复力均值赋值给矩阵z对应的元素，这样就得到了x，y，z三个同维矩阵，然后通过interp2()命令对全体数据进行二维插值。

插值后，观察三维模型的曲面图3(a)和恢复力等高线投影图3(b)，可以看出以位移和速度为变量的恢复力是一个形状并不复杂并且不闭合的坡形空间曲面。

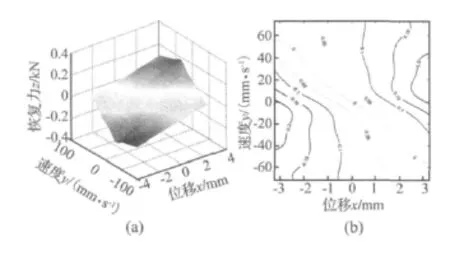
图3 拟合前恢复力的三维显示图和其等高线投影图Fig.3 The three-dimension graphics and the contour line chart of the restoring force before fitting

2.4 恢复力组成的分析和模型参数的辨识

根据金属橡胶的实际作用机理，结合数据的特点，此处把恢复力分解为只与位移有关的纯弹性力、只与速度有关的纯阻尼力和与速度有关的负刚度弹性力(后文有说明)，并根据数据分别进行拟合。

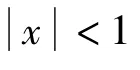
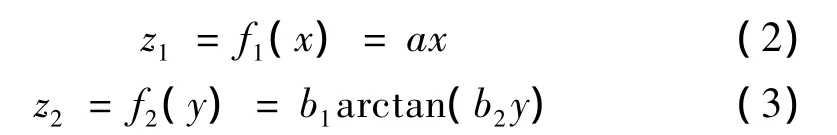
根据数据通过最小二乘法对待估参数进行拟合估计，得到各自的解析表达式如下:

拟合后曲线如图4中实线所示。

图4 纯刚度和纯阻尼曲线(圆点是拟合前数据，实线是拟合后数据)Fig.4 The curse of pure stiffness and pure damping(circle points are the data before fitting，solid line is the data after fitting)

在三维坐标系中表达式z1=f1(x)和z2=f2(y)都是空间曲面，绘出曲面z1和曲面z2，叠加曲面z4=z1+z2，差值曲面(此处设恢复力数据曲面是Z)z5=Z-(z1+z2)，如图5所示。

对恢复力数据曲面和叠加曲面的差值曲面进行详细分析和观察，如图6所示。通过分析可知，差值曲面函数关于位移和速度两个自变量近似为一个奇函数;在曲面存在的四个卦限内曲面峰值绝对值和形状都基本相同;当位移取正值时，差值曲面都是负值，当位移取负值时，差值曲面都是正值;并且在位移为零或速度为零时，差值曲面都取值为零，于是可以设计差值曲面函数为:

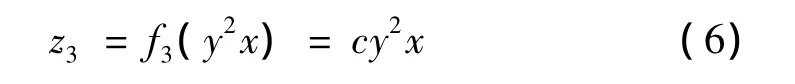
最小二乘法拟合后得到表达式:

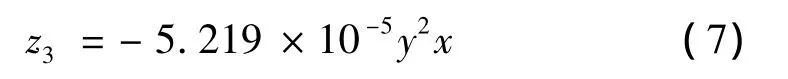
分别绘制差值曲面拟合前、后图和恢复力拟合前、后图，如图7所示。

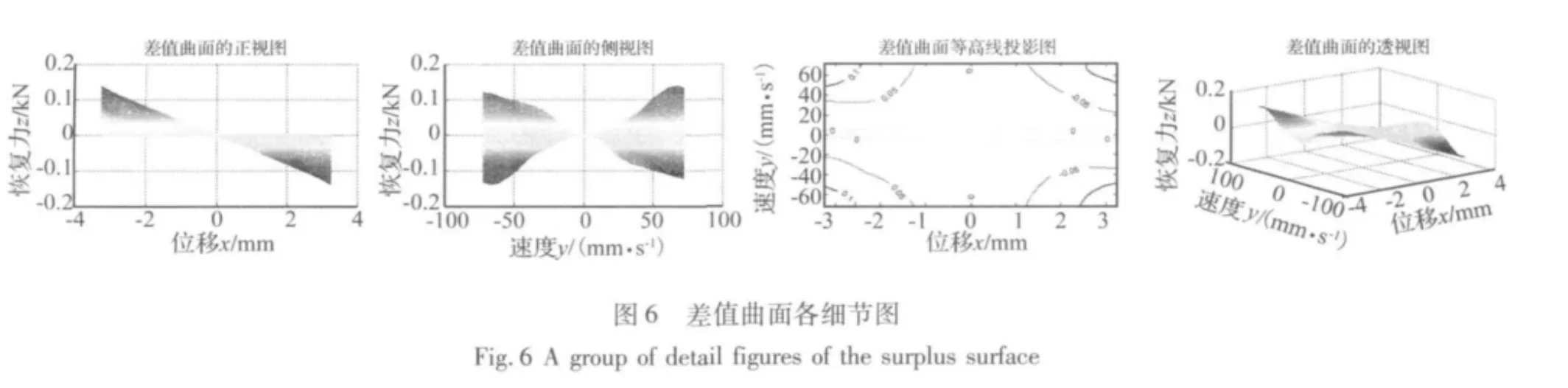
良好的拟合效果表明了金属橡胶材料恢复力中存在与速度平方项相关的负刚度弹性力成分。结合金属橡胶材料作用机理的复杂性和特殊性，初步分析认为至少有三个原因造成了这个结果:一是由于持续的形变，使金属橡胶材料产生了明显的蠕变松弛现象，内部金属丝勾连情况不再保持工作前状态，使材料在位移标定零点的位置出现了材料内部应力不平衡的现象，形成了类似鼓形薄壳体的负刚度结构;二是由于材料运动造成的金属丝滑移现象使开始工作前的试件边界状态发生了改变;三是试验中夹具质量和材料质量在运动时附加的惯性力产生的影响。

至此恢复力三维模型的建立和分析基本完成，本模型中恢复力由三个部分组成，分别是:正刚度线性弹性力、非线性阻尼力和与速度平方有关的非线性负刚度弹性力，方程解析表达式如下所示:

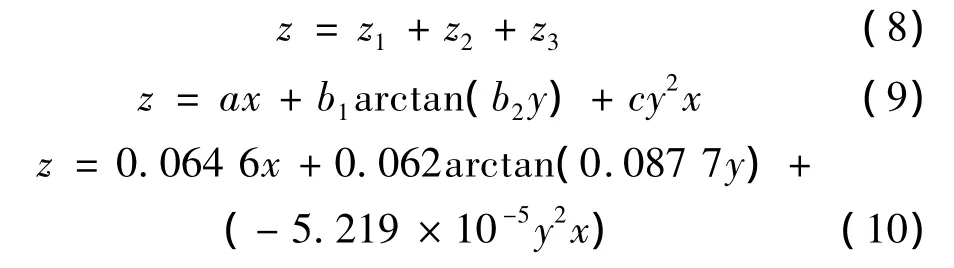
经大量实验分析可知，本模型对于对称结构的金属橡胶试件具有广泛适用性。但是由于金属橡胶材料的恢复力特性受到试件成型工艺参数、安装时的边界条件和试件变形形式的显著影响，因此模型中四个待估参数(a，b1，b2，c)也会受到上述因素的影响，在模型拟合时需要全面考虑，同时，如果存在加载后金属橡胶的自由平衡位置改变的情况，需要对模型进行修正，即在公式(9)的右边添加一个常数项d，d的辨识可由金属橡胶的静载实验给出，因为属于一般性的实验，在此不做赘述，修正后模型的结构形式如下所示:

3 模型的验证

选取试件工作范围的任意振幅频率的谐波激励作为实试验件，采集获得恢复力数据，对比三维模型的解析结果，以恢复力的定测值和解析值的相对误差平均值和相关系数两个指标作为评价标准，表2为所得结果。结果表明拟合精度很高，本模型中对恢复力的分析处理具有合理性，但是频率和振幅的增加在一定程度上会影响拟合精度，尤其频率影响更加明显。

表2 任意三种工况下的模型验证结果Tab.2 The results of model verification in three optional harmonic excitations

4 结论

本文建立了金属橡胶材料弹性恢复力的三维模型，本模型更加直观地反映了金属橡胶的刚度和阻尼特性，模型中恢复力是位移和速度的二元函数，既充分考虑了速度对恢复力的影响，也兼顾了多个离散谐波激励条件下恢复力特性的统一描述，为金属橡胶在任意激励下的力学特性研究和响应估计提供了一个新的研究思路，并为其他弹性阻尼元件的本构力学研究提供了新的方法，但是由于金属橡胶结构和力学特性的复杂性的影响，本模型在随机激励、高频、高温等条件下的应用仍有限制，并不是一个普适的模型，相关研究和分析是有待于进一步深化。

［1］ Menq C H，Bielak J，Griffin J H.The influence of a microslip on vibratory response.part I:a new microslip model and part II:a comparison with experimental results［J］.Journal of Sound and Vibration，1986，107(2):279-307.

［2］姜洪源，郝德刚，敖宏瑞.环形金属橡胶隔振器系统建模与实试验究［J］.湖南科技大学学报(自然科学版)，2005，20(1):13-16.

［3］ Masri S F.Forced vibration of the damped bilinear hysteretic oscillator［J］.J.the Acoustical Society of America，1995，57(1):106-112.

［4］Baber T T，Wen Y K.Random vibration of hysteretic degrading systems［J］.ASCE J.the Engineering Mechanics Division，1982，107:1069-1089.

［5］Badrakhan F.Dynamic analysis of yielding and hysteretic systems by polynomial approximation［J］.Journal of Sound and Vibration，1988，125(1):23-42.

［6］龚宪生，谢志江，骆振黄，等.非线性隔振系统阻尼特性研究［J］.振动工程学报，2001，14(5):334-338.

［7］白鸿柏，张培林，郑 坚，等.滞迟振动系统及其工程应用［M］.北京:科学出版社，2002:13-50.

［8］闻邦椿，李以农，徐培民，等.工程非线性振动［M］.北京:科学出版社，2007.

［9］白鸿柏，黄协清.含有三次非线性的粘性阻尼双线性滞迟隔振系统［J］.振动与冲击，1998，17(1):5-8.

［10］温诗铸，黄 平.摩擦学原理［M］.北京:清华大学出版社，2008.