等效时谐耦合场分析水轮发电机负序运行能力

姚缨英， 刘广

（浙江大学电气工程学院，浙江杭州 310027）

0 引言

发电机在不对称运行时，定子绕组中会产生负序电流，该负序电流会感生出一个与正序磁场旋转方向相反的负序磁场。其在发电机转子的切割下，会在阻尼绕组、励磁绕组及转子本体中感应出2倍工频的负序涡流，从而在发电机中产生附加热损耗［1］，引起发电机，尤其是转子的局部过热从而损坏发电机转子。发电机不对称运行时负序电流对发电机性能的影响极限称为发电机负序运行能力。阻尼绕组在发电机负序运行时起着屏蔽负序涡流的作用，因而其为发电机负序运行时温升最高、最容易烧伤的部件。随着发电机单机容量的不断提高，负序电流造成的危害程度也急剧增加，阻尼绕组烧伤的故障时有发生［2－3］。因此，大型发电机负序运行能力尤其是负序运行时阻尼绕组温度分布的研究已经成为大型发电机设计、制造、以及安全运行的关键之一，具有非常重要的理论意义和工程价值。

发电机负序运行能力的研究是涉及电机电磁场、温度场以及转子运动的综合性问题。目前，国内外对于发电机涡流场和温度场的研究方法大致可归结为3类:1）将电机磁场等效为“磁路”，用解析公式计算得到各部分的损耗，然后将损耗值代入等效的“热路”中，利用解析公式得出转子各部分温升［4－6］，这种方法误差相对较大，且不能得到温度分布，只能计算出温升;2）利用等效的“磁路”和解析公式得到各部分的损耗值，然后将所得损耗值作为负载，建立有限元模型得到最终的温度分布［7－9］，这种方法可以得到相应损耗下的温度分布，但是损耗的计算仍然具有较大误差;3）分别建立电磁场和温度场的有限元模型，利用电磁场得到的各部件损耗总值作为温度场的热源，求解出温度分布［10－11］，这种方法同样可得到相应损耗值下的温度分布，且损耗计算误差相对较小，但忽略了损耗在各导电部件内不均匀分布的实际。对于电机转子运动问题的处理一直是电机电磁场分析的难点和关键，方法主要有边界积分法、重新剖分法和运动边界法等［11－14］，但这几种方法都存在运算量比较大、对系统要求比较高、运算时间比较长等问题。

本文给出一种等效时谐场分析转子负序涡流场的方法，采用相对运动等效的原理将发电机的动态电磁场等效为准静态电磁场进行谐波分析，并用ANSOFT软件的时步动态分析对这种等效的可行性进行了验证。还对阻尼绕组气隙建模和损耗的耦合加载对求解阻尼绕组温度分布的影响进行了研究。建立了考虑阻尼绕组气隙的水轮发电机电磁场和温度场耦合有限元模型;利用顺序耦合的方法对一台容量为250 MW的水轮发电机进行了涡流场－温度场的耦合分析，得到了负序运行工况下的阻尼绕组温度分布，确定了其具有9%的稳态负序运行能力。

1 水轮发电机的有限元模型

1.1 水轮发电机电磁场有限元模型

忽略电机的端部效应，认为磁场在轴向方向是均匀分布的，将发电机电磁场问题简化为二维问题，并根据电机电磁场分布的特点，选取一个单元电机作为电磁场的计算区域，包括转子磁轭、转子磁极、励磁绕组、阻尼绕组、极靴及机身绝缘、定子铁心、定子绕组和各部分气隙等，其中着重考虑了阻尼绕组气隙的建模:在阻尼绕组与极靴之间建一个厚度为0.125 mm的圆环来模拟阻尼绕组气隙，如图1所示。

图1 发电机电磁场分析计算区域Fig．1 Calculate region of electromagnetic

时谐电磁场在求解区域内满足矢量位方程为

式中:A为磁矢量位;ν为媒质的磁阻率;Js为源电流密度;σ为电导率;ω为激励角频率;φ为标量电位。

二维情况下，磁矢量位A和源电流密度Js都只有 z轴分量，即 Ax=Ay=0，Jsx=Jsy=0。

式中:Az为磁矢量位的z轴分量;Jsz为源电流密度的z轴分量。

为模拟发电机在不对称运行时定子电流中负序分量在转子中产生的附加损耗以及温度分布，假设定子电流为频率为f的三相负序电流，将负序定子电流产生的旋转磁场与转子间的相对运动等效为相对静止的转子和频率为2f的定子三相对称电流。此时，上述边值问题可转化为时谐场模型，相应的泛函和条件变分为

式中:Az为频率2f的矢量磁位相应的相量;ω=2π×2f;σ为电导率。

对上述条件变分问题进行有限元离散，即可用来讨论水轮发电机负序磁场的影响。

1.2 水轮发电机转子温度场有限元模型

为了计算和分析的方便，对水轮发电机一对极的磁极系统作如下假设:

1）由于结构和风路的对称性，认为转子轴向中间断面为绝热面;

2）由于磁轭和磁极的交界面处有一气隙层，假设磁轭和磁极之间没有热交换，即此交界面为绝热面;

3）假设转子迎风面和被风面的风温呈线性变化，并用散热系数的差异等效风温的变化;

4）忽略阻尼条端环对阻尼绕组温度分布的影响;

5）阻尼绕组气隙虽然尺寸很小，但其对阻尼绕组与极靴之间的热传递有比较大的影响，因此在建模中对于这部分气隙予以考虑。

根据以上假设，同时考虑与电磁场的耦合，选择水轮发电机一对极的磁极系统的轴向中间断面作为其二维温度场的求解区域，包括转子磁极、励磁绕组、阻尼绕组、极靴及机身绝缘和阻尼绕组气隙等，其中一个极的求解区域如图2所示。

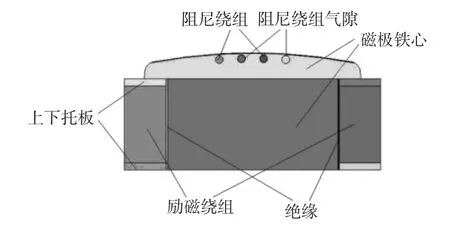
图2 转子温度场一个极的二维求解区域Fig．2 Calculate region of thermal of one pole

根据传热学理论，稳态运行时的电机转子在求解区域内遵循导热学基本定律和能量守恒定律，满足下面的微分方程，即

式中:T为物体的温度;k为物体的导热系数;q为热源密度。

在二维稳态的情况下，由于轴向中间断面为绝热面，不存在z轴方向的热传导，且忽略温度随时间的变化，上述微分方程可简化为

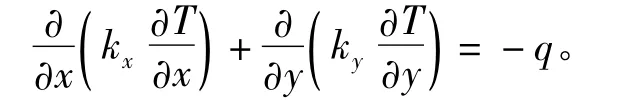
根据前面的假设，磁极和磁轭之间的交界面为绝热面S1，满足绝热面边界条件

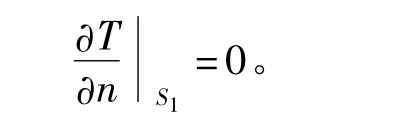
励磁绕组的迎风面、被风面以及极靴的迎风面、被风面和端面均为散热面S2，满足散热面边界条件

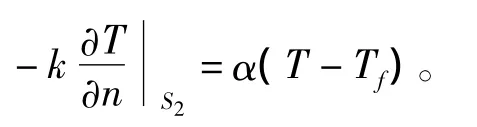
式中:Tf为周围介质温度;α为散热系数。

水轮发电机各部分的散热系数可由下式确定［15］，即

式中:α1为极靴表面散热系数;v为转子周速;α2为励磁绕组表面散热系数;α2（kf=1）与v有关;kf与定子铁心长度和极距有关。

针对迎风面与被风面的不同，假设风温呈线性变化，用一个比例系数k来对其进行区分。本文中迎风面的比例系数k1选择为1.1，被风面的比例系数k2选择为0.9。

由以上各式可知，二维稳态温度场的混合边值问题为

根据变分原理，上述混合边值问题可转化为相应的泛函和条件变分问题为

对上述条件变分问题进行有限元离散后，即可对水轮发电机二维温度场进行稳态分析和求解。

2 负载确定及求解设定

2.1 电磁场分析中转子运动问题的处理及各部分负载的确定

水轮发电机负序运行时，转子和负序磁场以相同的转速向不同方向旋转使电磁场分析非常困难，本文对两者的相对运动进行了等效:认为转子相对静止，而负序磁场以2倍的同步转速向相反的方向旋转;这样就相当于转子静止不动，而定子绕组中存在2倍工频的负序电流。以此来求解阻尼绕组中的负序涡流损耗与运用时步的方法求解运动问题相比占用更少的时间和资源，且求解精确度不会受到影响。

根据上述运动问题的处理方法可以确定电磁场分析需要施加的各部分负载如下:

1）在励磁绕组中不需要施加任何载荷。

2）在定子绕组中，给A、B、C三相施加负序电流对应的电流密度，并且各相之间相位角按照负序条件施加。

3）电磁场谐波分析的频率为2倍工频，即100 Hz。

2.2 温度场分析中各部分负载的确定

水轮发电机转子温度变化由磁极系统各部分的损耗发热所引起，因此，温度场的负载即发电机转子磁极的各部分损耗，其中包括:励磁绕组损耗、阻尼绕组损耗和磁极表面的附加损耗［15］。

Ⅰ）励磁绕组损耗

励磁绕组损耗是指励磁电流的电阻铜耗，即

其中:PCuf为励磁绕组铜耗;If为励磁电流;Rf为励磁绕组电阻。

Ⅱ）阻尼绕组损耗

着重考虑了阻尼绕组损耗分布对阻尼绕组温度分布的影响。首先，电磁场分析和温度场分析时，转子的剖分是完全相同的，然后采用顺序耦合的方式，通过对应的单元和节点直接将磁场分析的结果耦合到温度场分析中，从而获得更加精确阻尼绕组损耗的分布。阻尼绕组一个剖分单元的涡流和损耗分别为

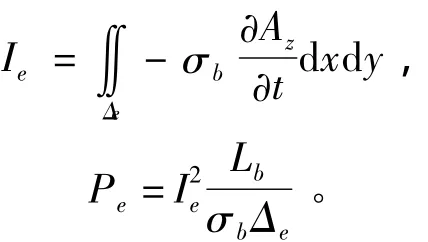
其中:σb为阻尼绕组电导率;Lb为阻尼条长度;Δe为阻尼绕组一个剖分单元的面积。

Ⅲ）磁极表面附加损耗

在建模时考虑了阻尼绕组与极靴之间的小气隙，因此磁极表面附加损耗对于阻尼绕组的温升影响较小，予以忽略。

2.3 电磁场－温度场的顺序耦合求解

采用顺序耦合的方法对水轮发电机负序运行时的电磁场和温度场进行耦合分析，首先，分别定义电磁场和温度场的物理环境;然后，对电磁场进行有限元分析;最后，将电磁场的结果作为负载施加到温度场中对温度场进行有限元分析，得到水轮发电机负序运行时的转子温度场分布，顺序耦合的数据流程如图3所示。

图3 顺序耦合数据流程图Fig．3 Data flow diagram of sequence coupling

阻尼绕组的涡流损耗是由定子绕组的负序电流感应产生的，由于集肤效应的影响，其在阻尼绕组内部是不均匀分布的，非耦合场分别求解的方法默认阻尼绕组损耗均匀分布于阻尼绕组内部，其求解的温度分布不够精确，而顺序耦合方法则以单元为单位加载阻尼绕组损耗负载，能够得到更为精确的阻尼绕组温度分布。

3 方法验证以及计算结果的分析

3.1 等效时谐法计算转子负序涡流场正确性的验证

为了验证本文所采用的“等效时谐场分析转子负序涡流及其温度场”的可行性，用ANSOFT软件按照场－路－运动耦合时步有限元法对同一问题进行了计算。针对如图4所示的求解区域，分别采用时步运动电磁场求解和等效时谐场求解，并对求得的阻尼绕组损耗结果（见图5、图6）及求解所用时间进行对比。

图4 水轮发电机一个极的有限元模型Fig．4 Finite element model of a pole

图5 时步运动电磁场求解的阻尼绕组涡流损耗密度Fig．5 Eddy current loss density of the damper winding based on time stepping electromagnetic field

图6 稳态涡流场求解的阻尼绕组涡流损耗密度Fig．6 Eddy current loss density of the damper winding based on eddy current field

由图5可知，进行时步运动电磁场分析时，阻尼绕组的涡流损耗在负序运行1 s后达到稳定。稳定后的时步运动电磁场求解结果与100 Hz下的等效时谐场求解结果如表1所示。

表1 不同方法求解的阻尼绕组涡流损耗密度Table 1 Eddy current loss density of the damper winding based on different methods （W/m）

由上表可知，时步运动电磁场的求解结果和稳态涡流场的求解结果基本相同，因此在水轮发电机负序运行时对转子的旋转进行相对运动等效处理是完全可行的;同时在相同的网格密度下以0.001 s为步长对时步运动电磁场求解1.5 s大约耗时1 h，而稳态涡流场的求解耗时不到5 min，因此采用等效时谐法在计算工作量方面具有一定优势。

3.2 水轮发电机转子负序涡流场计算结果与分析

采用相对运动等效的时谐分析方法对本文建立的水轮发电机一对极的电磁场模型进行计算，磁场分布如图7和图8所示，从中可见，各阻尼绕组及其附近气隙处的磁场大小并不相同，因此阻尼绕组中损耗的大小也各不相同。

综合图9和表2，可得水轮发电机负序运行时阻尼绕组损耗的分布规律:

1）两个磁极的阻尼条损耗分布几乎是完全对称的，分布规律相同且损耗值大小基本相等。

2）对于每一个磁极，损耗集中于磁极两侧的两根阻尼条上，中间两根阻尼条损耗较小，且位于转子旋转方向最后方的阻尼条损耗最大，位于转子旋转方向前方第二根阻尼条损耗最小。

3）对于每一根阻尼条，损耗分布极不均匀，且损耗集中分布在阻尼条糟口附近。

图7 电磁场的实部和虚部磁力线图Fig．7 Flux density of the poles

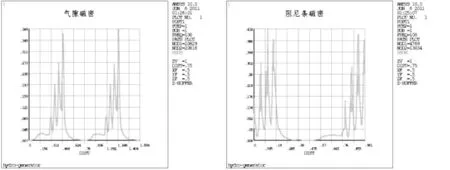
图8 气隙磁密曲线和阻尼绕组磁密曲线Fig．8 Flux density curves of the air-gap and the damper winding

图9 一对磁极阻尼绕组损耗分布Fig．9 Eddy current loss distribution of a couple of poles

表2 负序运行时各阻尼条损耗密度Table 2 Eddy current loss density of damper windings on negative sequence （W/m）

3.3 温度场求解结果与分析

为研究阻尼绕组气隙建模和耦合场加载阻尼绕组损耗对求解阻尼绕组温度分布的影响，分别按照不考虑阻尼绕组气隙建模耦合场求解、考虑阻尼绕组气隙建模非耦合场求解、以及考虑阻尼绕组气隙建模耦合场求解进行温度分布计算，温度分布以及各阻尼条的温升如图10～图15以及表3所示。

图10 不考虑阻尼绕组气隙建模的耦合场总体温度分布Fig．10 Temperature distribution of the poles based on coupling fieldswithoutdamperwindingairgap modeling

图11 不考虑阻尼绕组气隙建模的耦合场阻尼条温度分布Fig．11 Temperature distribution of the dampers based on coupling fieldswithoutdamper winding airgap modeling

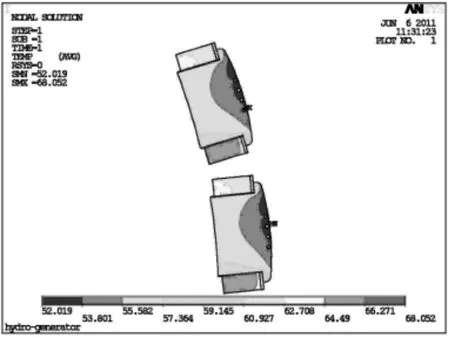
图12 考虑阻尼绕组气隙建模的非耦合场总体温度分布Fig．12 Temperature distribution of the poles based on non-coupling fields with damper winding airgap modeling

图13 考虑阻尼绕组气隙建模的非耦合场阻尼条温度分布Fig．13 Temperature distribution of the dampers based on non-coupling fields with damper winding airgap modeling

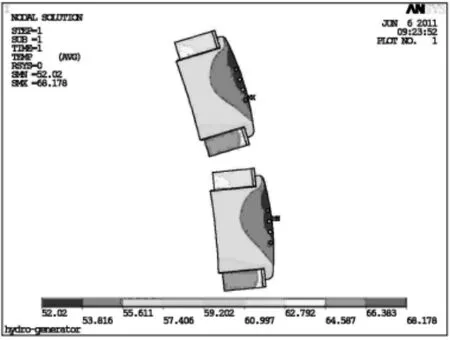
图14 考虑阻尼绕组气隙建模的耦合场总体温度分布Fig．14 Temperature distribution of the poles based on coupling fields with damper winding air-gap modeling

图15 考虑阻尼绕组气隙建模的耦合场阻尼条温度分布Fig．15 Temperature distribution of the dampers based on coupling fields with damper winding air-gap modeling

1）对比不考虑阻尼绕组气隙建模耦合场和考虑阻尼绕组气隙建模耦合场的结果可以发现，前者阻尼绕组温升明显偏低，而且两侧阻尼条由于与极身之间存在良好的热交换造成温升不明显，与实际情况不符;

2）对比考虑阻尼绕组气隙建模非耦合场和考虑阻尼绕组气隙建模耦合场的结果可以发现，前者由于没有考虑损耗在阻尼条内的不均匀分布，造成各根阻尼条内部温升相同且最高温升稍稍偏低。

综合以上几种情况，将计算结果与同类型水轮机设计和运行经验值相比较，本文采用的考虑阻尼绕组气隙建模的耦合场求解结果最能反映实际情况。

3.4 水轮机负序运行能力

由考虑阻尼绕组气隙建模的耦合场求解结果可得水轮发电机9%负序运行时，阻尼绕组的温度分布规律如下:

1）各个磁极之间阻尼绕组温度分布完全对称，分布规律相同且温升值大小近似。

2）对于单个磁极，磁极两侧阻尼条温升较大且靠近被风面的一根温升最高，中间两阻尼条温升较小且温升值基本相同。

3）单根阻尼条内部温度分布不均匀，但温度相差不大。

本文分析的250 MW的水轮发电机阻尼绕组的最高温升为68.178℃，远远低于阻尼条材料的最高耐热温度，因此该水轮发电机具有9%的稳态负序运行能力。

表3 各根阻尼条的温升值Table 3 Temperature rise of the dampers on different situation （℃）

4 结论

本文通过有限元分析得到以下结论:

（1）等效时谐法采取相对运动等效处理水轮发电机负序运行时的转子旋转问题是完全可行的，可以正确计算转子负序涡流场，并且计算量较动态时步有限元法小得多。

（2）阻尼条绕组气隙对阻尼绕组的温度分布具有较大影响，建模时应予以考虑。

（3）耦合场加载阻尼绕组损耗更能反映阻尼绕组内部损耗分布不均的实际，可以得到更为精确的阻尼绕组温度分布。

（4）本文所计算的样机具有9%的稳态负序运行能力，符合设计标准。

［1］周光厚，侯小全．东方600MW汽轮发电机负序能力研究［J］．东方电气评论，2004，18（1）:20 －23．

ZHOU Guanghou，HOU Xiaoquan．Research on negative sequence capacity of dongfang 600MW turbogenerator［J］．Dongfang Electric Review，2004，18（1）:20－23．

［2］邓莉影．飞来峡机组阻尼条熔断的设计分析［J］．水电站机电技术，2003（3）:12－14．

［3］廖旭升．水轮发电机转子阻尼绕组温升过高的原因综述［J］．广西水利水电，2007（2）:49－50．

LIAO Xusheng．Analysis of too high temperature rise of turbine generator rotor damper winding［J］．Guangxi Water Resources ＆Hydropower Engineering，2007（2）:49 －50．

［4］Hammons T J．Comparison of losses and heating generator rotors following sever supply system disturbances［J］．IEEE Transactions on Energy Conversion，1999，5（4）:703－712．

［5］Zhi Gao，Habetler T G，Harley R G．A complex space vector approach to rotor temperature estimation for line-connected induction machines with impaired cooling［J］．IEEE Transactions on Industrial Electronics，2009，56（1）:239 －247．

［6］赵凤山，史乃．瞬态不对称负荷下水轮发电机阻尼绕组的温升计算［J］．哈尔滨电工学院学报，1989，12（1）:1 －11．

ZHAO Fengshan，SHI Nai．The calculation of the damping winding temperature rise of waterwheel generator under transient unbalanced faults［J］．Journal of Harbin Institute of Electrical Technology，1989，12（1）:1－11．

［7］李伟力，周封，侯云鹏，等．大型水轮发电机转子温度场的有限元计算及相关因素的分析［J］．中国电机工程学报，2002，22（10）:85－90．

LI Weili，ZHOU Feng，HOU Yunpeng，et al．Calculation of rotor temperature field for hydro-generator as well as the analysis on relevant factors［J］．Proceedings of the Chinese Society for Electrical Engineering，2002，22（10）:85－90．

［8］付敏，李伟力，张东．水轮发电机气隙内磁场和转子温度场计算［J］．哈尔滨工业大学学报，2003，35（9）:1311 －1134．

FU Min，LI Weili，ZHANG Dong．Calculation for electromagnetic field and rotor temperature field inside air gap of hydroelectric generator［J］．Journal of Harbin Institute of Technology，2003，35（9）:1311－1134．

［9］HUO Feiyang，LI Weili，ZHANG Yu．Calculation of damper winding loss and influence on large hydro-generator temperature［C］//2010 International Conference on Computer Application and System Modeling，October 22－24，2010，Taiyuan，China．2010，（4）:365－369．

［10］范镇南．基于电磁场与温度场计算的贯流式水轮发电机阻尼系统损耗发热研究［D］．重庆:重庆大学电气工程学院，2007．

［11］韩力．大型水轮发电机损耗、发热与通风问题的研究［D］．重庆大学电气工程学院，2008．

［12］张洋．三维瞬态涡流场－电路－运动系统耦合问题的研究［D］．沈阳:沈阳工业大学电气工程学院，2008．

［13］韩力，辛懋，谢红，等．一种模拟实测过程的齿槽转矩数值计算方法［J］．电机与控制学报，2007，11（6）:589 －593，599．

HAN Li，XIN Mao，XIE Hong，LI Hui，et al．Numerical method for calculating cogging torque by simulation of actual measurement［J］．Electric Machine and Control，2007，11（6）:589 －593，599．

［14］刘秀君，李伟力，陈文彪．三相异步起动永磁同步电动机起动特性［J］．电机与控制学报，2006，10（3）:269 －274．

LIU Xiujun，LI Weili，CHEN Wenbiao．Analysis of starting characteristics of therr-phase line-start permanent magnet synchronous motor［J］．Electric Machine and Control，2006，10（3）:269 －274．

［15］ 白延年．水轮发电机设计与计算［M］．北京:机械工业出版社，1982:119－170．

（编辑:刘素菊）