无刷双馈电机转矩和转速的无源性控制

韩力， 潘红广， 刘航航， 罗杰， 王华

（重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

无刷双馈电机（brushless doubly-fed machine，BDFM）作为一种新型的交流调速电机，去掉了电刷和滑环，具有转子结构坚固、变频器容量小、功率因数和转速可调、系统运行和维护成本低等优点，在电动机变频调速控制以及发电机变速恒频控制领域具有广阔的应用前景［1］。然而，BDFM系统又体现出多变量、非线性、强耦合等特点，高性能的控制策略是促进BDFM推广应用的关键。目前交流电机常用的高性能控制方法主要有两种，即矢量控制（vector control，VC）和直接转矩控制（direct torque control，DTC）。矢量控制可以实现磁通和转矩的解耦控制，动态性能好，不足之处是控制结构复杂，计算量大，控制效果易受转子参数变化的影响。1971年Blaschke等人首先提出了感应电机的矢量变换控制方法［2］，从理论上解决了感应电机磁通和转矩的解耦控制。1994年Zhou等人采用转子磁场定向的原理，将矢量控制应用到 BDFM中［3］，通过控制功率绕组和控制绕组之间的同步角实现转速的控制，仿真结果表明该方法具有良好的动态性能，但却增加了系统的复杂性和计算量。之后又先后提出了简化的矢量控制方法［4－5］和定子磁场定向的矢量控制方法［6］。直接转矩控制是继矢量控制之后发展起来的另一种高性能交流电机控制方法，该方法具有鲁棒性好、控制结构简单等优点，不足之处是转矩脉动大。直接转矩控制理论是1977年由Ptunkett等人首先提出的，1986年Tankahashi等人在感应电机的控制中获得了成功应用［7］。1996年Brassfield等人将直接转矩控制应用到BDFM的控制中［8］，2007年Sarasola等人提出了转矩预测控制的直接转矩控制方法［9－10］，仿真结果表明于该方法可以有效减小转矩脉动，但低速时转矩和转速仍然存在较大波动。

无源性控制（passivity-based control，PBC）是一种全新的非线性控制方法，它最早应用于机器人控制。无源性控制方法具有优越的控制性能，它从能量的角度出发，通过配置系统能量耗散特性方程中的无功分量，迫使系统总能量跟踪期望的能量函数，并使系统的状态变量渐进收敛至设定值。这是一种注重系统物理特征自然属性的方法，可有效简化控制器的设计，提高系统的鲁棒性，且控制器的设计是全局定义且全局稳定的［11］。文献［12］采用感应电机的三阶模型，分析了磁链子系统的无源性并设计了相应的控制器，仿真结果表明该方案能保证转矩、转子磁链及转速的渐进跟踪;文献［13］在考虑磁饱和的情况下，对感应电动机的转矩和磁通追踪问题进行了研究;文献［14］研究了双馈风力发电机的无源性控制问题;文献［15］研究了永磁同步电机的无传感器无源性控制方法，获得了很好的效果。

本文以笼型转子BDFM为研究对象，针对其多变量、非线性、强耦合的特点，为了简化控制结构并进一步提高控制性能，从三相静止坐标系下的电压方程出发，经过分析推导建立了dq轴旋转坐标系下电压、磁链和转矩的数学模型，进而建立了与控制绕组子系统电压方程相对应的欧拉－拉格朗日（Euler-Lagrange，方程，并对其无源特性进行了分析。在此基础上，根据无源性控制的基本理论，设计了相应的转矩和转速控制器，并在设计中通过增加状态变量的阻尼项以改善系统的动态响应性能。最后，对两台样机进行仿真分析并与矢量控制、直接转矩控制进行对比，以验证本文所提控制策略的正确性和有效性。

1 BDFM的数学模型

1.1 三相静止坐标系模型和dq轴旋转坐标系模型

BDFM的定子上嵌放有2套彼此独立的三相对称绕组，其中1套是极对数为pp的功率绕组，它直接与电网联接，其频率fp恒定;另1套是极对数为pc的控制绕组，由变频电源供电，其频率 fc可调。定子功率绕组和控制绕组在理论上没有直接的电磁耦合，而是通过转子绕组的磁场调制作用来实现机电能量转换。在ABC三相静止坐标系下，BDFM的电压方程可表示为

式中:up、ip、Zp分别为定子功率绕组的电压、电流和阻抗矩阵;uc、ic、Zc分别为定子控制绕组的电压、电流和阻抗矩阵;ur、ir、Zr分别为转子绕组的电压、电流和阻抗矩阵;Zpr、Zcr分别为定子功率绕组、控制绕组与转子绕组间的互阻抗矩阵。

为了便于将ABC三相静止坐标系下的电压方程变换到转子速dq轴旋转坐标系下，现将BDFM分为功率绕组子系统和控制绕组子系统。在BDFM的磁场转换处于理想情况下时，可假设转子电压、电流、电阻和电感分别满足以下关系［16］，即

式中:uqr、udr、iqr、idr、Rr、Lr分别为转子电压、电流的q轴和d轴分量以及转子的电阻和电感;uqrp、udrp、iqrp、idrp、Rrp、Lrp分别为功率绕组子系统中转子电压、电流的q轴和d轴分量以及转子的电阻和电感分量;uqrc、udrc、iqrc、idrc、Rrc、Lrc分别为控制绕组子系统中转子电压、电流的q轴和d轴分量以及转子的电阻和电感分量。

由式（1）和式（2），根据坐标变换理论，经过一系列的分析推导，可得到转子速dq轴旋转坐标系下功率绕组和控制绕组子系统的电压方程和磁链方程为

式中:uqp、udp、iqp、idp、ψqp、ψdp分别为功率绕组电压、电流和磁链的 q 轴和 d 轴分量;uqc、udc、iqc、idc、ψqc、ψdc分别为控制绕组电压、电流和磁链的q轴和d轴分量;ψqrp、ψdrp、ψqrc、ψdrc分别为功率绕组和控制绕组子系统中转子磁链的q轴和d轴分量;Rp、Lp、Mpr分别为功率绕组的电阻、自感以及与转子绕组之间的互感;Rc、Lc、Mcr分别为控制绕组的电阻、自感以及与转子绕组之间的互感;ωr为转子机械角速度;p为微分算子。

BDFM的电磁转矩为

式中:Tep和Tec分别为功率绕组子系统和控制绕组子系统产生的电磁转矩。

BDFM的机械运动方程为

式中:J、Kd、TL分别为转子的转动惯量、阻尼系数和负载转矩。

由于式（3）～式（7）处于转子速dq轴旋转坐标系中，控制绕组、功率绕组中的各变量如电压、电流、磁链等相对于转子仍然是交流量。为了便于控制，把它们变换到各自的同步速dq轴旋转坐标系下，便可获得便于处理的直流特性。图1给出了功率绕组同步速旋转坐标系、控制绕组同步速旋转坐标系与转子速旋转坐标系之间的变换关系，图中d、q、ω分别代表d轴、q轴和角速度;上标p、c、r分别代表功率绕组同步速旋转坐标系、控制绕组同步速旋转坐标系和转子速旋转坐标系，下标p、c、r分别代表功率绕组、控制绕组和转子的变量;θp、θc分别为转子速旋转坐标系和同步速旋转坐标系之间的夹角，即=－ pt

式中:ωp、ωc分别为功率绕组和控制绕组的角频率;ωsp、ωsc分别为功率绕组和控制绕组的转差角速度。

图1 BDFM的dq轴旋转坐标系Fig．1 Dq-axis rotating reference frames of BDFM

转子速旋转坐标系和功率绕组同步速旋转坐标系以及控制绕组同步速旋转坐标系之间的变换关系分别为

式中f可表示电压、电流、磁链等变量。

通过上述变换，功率绕组子系统和控制绕组子系统在其各自的同步速dq轴旋转坐标系下的电压方程可分别化为

功率绕组子系统和控制绕组子系统的磁链方程在各自的同步速dq轴旋转坐标系的表达式变为

功率绕组子系统和控制绕组子系统的电磁转矩分量在各自的同步速旋转坐标系的表达式变为

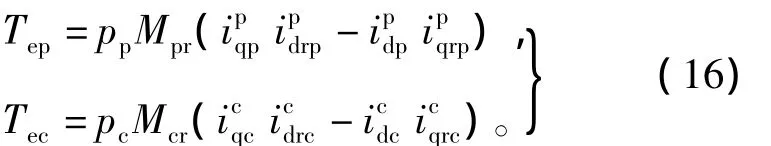
1.2 欧拉－拉格朗日方程

无源性控制方法和其它方法相比，在形式上具有显著的不同，它采用欧拉－拉格朗日方程来描述控制对象的数学模型。考虑到功率绕组直接和电网相联接，其电压幅值和频率恒定，对转速、转矩等目标的控制是通过调节控制绕组的电压幅值和频率来实现的。因此，将控制绕组子系统作为分析对象，将式（13）整理成欧拉－拉格朗日方程的形式，可得到电流的状态方程为

式中:u和i分别为控制绕组子系统的输入电压列矢量和输出电流列矢量;M和R分别为控制绕组子系统的电感矩阵和电阻矩阵;W为与控制绕组子系统有关转速和磁链乘积的项;I2为单位矩阵;J2和B分别为反对称矩阵。

1.3 系统的无源性分析

定义BDFM控制绕组子系统电气部分的能量存储函数为

将式（18）对时间求导，得

将式（17）代入式（19）中，得

由于B为反对称矩阵，故有iTBi=0，则Bi项对系统的能量平衡不起作用，也不影响系统的稳定性，故称该项为“无功力”，在进行状态反馈控制器设计时无需被抵消，因此简化了系统控制规律的设计。

对式（20）两端积分，得

式（21）为能量平衡方程，等号左边是控制绕组电气子系统磁场储能的增量，等号右边第一项为变频器供给控制绕组电气子系统的电能、第二项为控制绕组电气子系统消耗的电阻损耗、第三项为控制绕组电气子系统转化为机械能的部分。式（21）表明，控制绕组电气子系统磁场储能的增量总是小于控制绕组电源的供电能量，系统是严格无源的。

图2给出了功率绕组电气子系统、控制绕组电气子系统和机械子系统三部分的相互连接关系，虚线框内的控制绕组电气子系统和机械子系统构成了反馈互联结构，这是一个可控的部分。设计PBC方法可把控制绕组电气子系统的能量存储函数作为总的能量函数，而把机械子系统看作是电气子系统的无源干扰［11］。

图2 BDFM的反馈互联结构Fig．2 Feedback interconnection of BDFM

2 无源控制器的设计

2.1 转矩控制器的设计

定义控制绕组子系统的电流期望值为

同理，以下凡是变量上标带*号的都定义为期望值，凡是变量上标带～号的都定义为误差值。

选取控制绕组子系统的误差能量函数为

则控制绕组子系统的误差电流为

通过期望的电流矢量i*来获得期望的电磁转矩，将式（23）代入式（17），可得电流的误差方程为

由于B为反对称矩阵，所以上式右边第一项等于零，于是有

通过设定，使扰动量η=0，考虑到R为正定矩阵，由式（28）可知，＜0。根据李雅普诺夫稳定性定理可知［17］，误差电流必将收敛于0。再由电流和电磁转矩的关系式（16）可知，电磁转矩最终也将收敛于期望值。

借用磁场定向的方法来确定功率绕组电流的期望值。将功率绕组的磁链与其对应的同步速旋转坐标系的d轴重合，则由式（14）可得

由于功率绕组直接与工频电网连接，其电抗压降远大于电阻压降，因此在计算功率绕组磁链时，可忽略其电阻压降，得到以下关系，即

转子电流在各自的同步速旋转坐标系下，仍具有式（2）的关系。由式（2）和式（29）可得到功率绕组电流的期望值为

为了实现转子磁场和电磁转矩的渐进跟踪，制定如下控制目标:

1）电磁转矩渐进跟踪

考虑到式（13）中的所有电流均变换成了直流量，由式（13）中的第3行，可得到控制绕组的转差角速度为

由式（13）中的第1行、第2行及式（37），令扰动量η=0，则最后可得到PBC系统的控制规律为

式中:k1、k2是为了提高系统的动态响应性能而增加的阻尼系数。

2.2 转速控制器的设计

通过电流环的设计，实现电流的跟踪控制。在电流环之外设计速度环，实现转速的跟踪控制。基于无源性的BDFM转矩控制系统可渐进跟踪时变的负载转矩，因此转速调节器的设计就变得很简单，只需建立转速误差反馈，采用PI调节器，就可得到控制规律为

式中kp、ki分别为比例和积分增益。

根据以上分析，可得到整个控制系统的结构如图3所示。

图3 BDFM的无源性控制结构Fig．3 PBC structure of BDFM

3 仿真结果及分析

为了验证上述控制方法的正确性和有效性，本文选取两台BDFM样机，在Matlab/SIMULINK平台上进行仿真实验，并分别与矢量控制和直接转矩控制的效果进行对比分析。

3.1 矢量控制与无源性控制的对比

文献［5］采用矢量控制方法对BDFM进行控制，样机参数为:pp=3，pc=1，Rp=14.04 Ω，Lp=0.790 4 H，Mpr=3.379 mH，Rc=9.8 Ω，Lc=1.295 H，Mcr=7.141 mH，Rr=0.339 mΩ，Lr=0.06 mH，J=0.003 8 kg·m2，Kd=0。仿真过程如下:BDFM的初始转速给定为750 r/min，空载启动，1 s时加5 N·m的阶跃负载，2 s时转速给定突增到900 r/min，3 s时转速给定突降到600 r/min。采用基于同步角的矢量解耦控制方法，得到的转速和电磁转矩动态响应特性如图4 所示［5］。

图4 矢量控制的动态响应特性Fig．4 Dynamic response characteristics of VC method

采用无源性控制方法对同一台样机进行仿真，控制器参数取为 k1=k2=1 000，kp=153，ki=0.025，控制绕组子系统中转子磁链的给定值取为0.7 Wb，并假设 Rrp=Rrc=0.5 Rr、Lrp=Lrc=0.5 Lr，得到的仿真结果如图5所示。对比图4和图5可见，无源性控制方法对BDFM的控制是有效的，而且比矢量控制方法具有更加优越的动态响应性能。尽管在起动时超调量更大一些，但转速和电磁转矩的调节时间更短，在转矩发生波动时转速具有更高的鲁棒性，在转速发生波动时转矩的冲击更小。同时，由图5（c）可见，控制绕组子系统中转子磁链的实际值能够很好的跟踪给定值。此外，由于无源性控制方法避免了同时计算转子位置角、功率绕组同步角、转子位置角期望值及对控制绕组同步角的实时求导运算，从而使得该方法的计算量明显减少。

图5 无源性控制的动态响应特性Fig．5 Dynamic response characteristics of PBC method

3.2 直接转矩控制与无源性控制的对比

文献［10］采用直接转矩控制方法，样机参数为:pp=3，pc=1，Rp=0.81 Ω，Lp=80 mH，Mpr=0.89 mH，Rc=0.81 Ω，Lc=630 mH，Mcr=4.3 mH，Rr=1.57 Ω，Lr=0.04 mH，J=0.02 kg·m2，Kd=0。仿真过程如下:系统给定转速为亚同步速580 r/min，在2 s时突增至超同步速850 r/min，在3 s时突加负载8 N·m。采用转矩预测的直接转矩控制，得到的转速和电磁转矩动态响应特性如图6所示［10］。

图6 直接转矩控制的动态响应特性Fig．6 Dynamic response characteristics of DTC method

为了进一步验证无源性控制方法的有效性，对同一台样机进行仿真，控制器参数取为k1=k2=190，kp=125，ki=0.03，仿真结果如7所示。对比图6和图7可见，无源性控制方法在转速给定发生变化时具有更快的动态响应性能，且转矩的波动明显小于直接转矩控制方法，转矩的稳态误差更小。同时，由于后者无需扇区判别、磁链观测等环节，只需普通的处理器就可实现对BDFM的准确控制，体现出明显的优越性。

图7 无源性控制方法的动态响应特性Fig．7 Dynamic response characteristics of PBC method

4 结论

采用非线性控制方法中的无源性控制理论，实现了笼型转子BDFM转矩和转速的准确控制。从能量的角度出发，通过配置BDFM控制绕组子系统能量方程中的无功分量，迫使系统总能量跟踪期望的能量函数，使电流状态变量渐进收敛于期望值，有效简化了控制器的设计。在转矩控制器的设计中增加了状态变量的阻尼项，从而使系统的动态响应性能大为改善。通过对比发现，无源性控制比矢量控制具有更高的鲁棒性和更小的计算量，比直接转矩控制具有更小的转矩波动，表明该方法是笼型转子BDFM的一种优越的控制方案。

［1］ MCMAHON R A，ROBERTS P C，WANG X，et al．Performance of BDFM as generator and motor［J］．IEE Proceedings on Electric Power Applications，2006，153（2）:289 －299．

［2］BLASCHKE F．A new method for the structural decoupling of A．C．induction machines［C］//2nd IFAC Symposium on Multivariable Technical Control Systems，October 11 －13，1971，Dusseldorf，West Germany．1971:1 －15．

［3］ZHOU D，SPEE R．Synchronous frame model and decoupled control development for doubly-fed machines［C］//Proceedings of the 1994 25th Annual IEEE Power Electronics Specialists Conference，June 20－24，1994，Taipei，Taiwan．1994:1229 －1236．

［4］ZHOU D，SPEE R，ALEXANDER G C，et al．A simplified method for dynamic control of brushless doubly-fed machines［C］//Proceedings of the 1996 IEEE 22nd International Conference on Industrial Electronics，Control，and Instrumentation，August 5 －10，1996，Taipei，Taiwan．1996:946 －951．

［5］杨向宇，申辉阳．无刷双馈电机的一种矢量解耦控制［J］．电机与控制学报，2005，9（5）:409 －413．

YANG Xiangyu，SHEN Huiyang．A simple and practical vector decoupled control of brushless doubly-fed machines［J］．Electric Machines and Control，2005，9（5）:409 －413．

［6］SHAO S，ABDI E，BARATI F，et al．Stator-flux-oriented vector control for brushless doubly fed induction generator［J］．IEEE Transactions on Industrial Electronics，2009，56（10）:4220－4228．

［7］NOGUCHI T，TAKAHASHI I．A new quick-response and high efficiency control strategy of an induction machine［J］．IEEE Transactions on Industry Applications，1986，22（5）:820－827．

［8］BRASSFIELD W R，SPEE R，HABETLER T G．Direct torque control for brushless doubly-fed machines［J］．IEEE Transactions on Industry Applications，1996，32（5）:1098 －1104．

［9］SARASOLA I，POZA J，RODRIGUEZ M A，et al．Predictive direct torque control for brushless doubly fed machine with reduced torque ripple at constant switching frequency［C］//2007 IEEE International Symposium on Industrial Electronics，June 4 － 7，2007，Caixanova-vigo，Spain．2007:1074－1079．

［10］张爱玲，张洋．基于转矩预测控制的无刷双馈电机直接转矩控制系统［J］．电机与控制学报，2007，11（4）:326－330．

ZHANG Ailing，ZHANG Yang．Direct torque control for brushless doubly-fed machine based on torque predict control strategy［J］．Electric Machines and Control，2007，11（4）:326 －330．

［11］NICKLASSON P J，ORTEGA R，ESPINOSA P G，et al．Passivity-based control of a class of Blondel-Park transformable electric machines［J］．IEEE Transactions on Automatic Control，1997，42（5）:629－647．

［12］王涛，肖建，李冀昆．感应电机无源性分析及自适应控制［J］．中国电机工程学报，2007，27（6）:31－34．

WANG Tao，XIAO Jian，Li Jikun．Passivity analysis of induction motor and adaptive control［J］．Proceedings of the CSEE，2007，27（6）:31－34．

［13］FATTAH H A A，LOPARO K A．Passivity-based torque and flux tracking for induction motors with magnetic saturation［J］．Automatica，2003，39（12）:2123－2130．

［14］LOPEZ G I，JIMEENEZ M V M，CAMPERO L E，et al．Passivity based control of doubly-fed induction generators in wind turbines［C］//7th Electronics，Robotics and Automotive Mechanics Conference，September 28 － October 1，2010，Cuernavaca，Mexico．2010:607－612．

［15］BELABBES B，FELLAH M K，LOUSDAD A，et al．Passivity based control with orientation of the flux of a permanent magnet synchronous motor without mechanical sensor［J］．Acta Electrotechnica et Informatica，2009，9（2）:51－58．

［16］邓先明．无刷双馈电机的电磁分析与设计应用［M］．北京:机械工业出版社，2008:119－119．

［17］ 刘豹，唐万生．现代控制理论．3版［M］．北京:机械工业出版社，2006:163－170．

（编辑:刘素菊）