无轴承永磁同步电机径向悬浮力动态解耦控制

孙晓东， 朱熀秋， 张涛， 杨泽斌

（江苏大学电气信息工程学院，江苏镇江 212013）

0 引言

无轴承永磁同步电机是将无轴承技术应用于普通永磁同步电机的一种电机，在永磁同步电机基础上，将产生径向悬浮力的磁轴承绕组（线圈）和电机定子绕组叠压在一起，实现电机的无轴承化。无轴承永磁同步电机不仅具有效率高、功率因数高、体积小、重量轻、控制性能好等优点，而且具有磁轴承无摩擦、无磨损、不需润滑、高转高精等优点，从而使其在生物医药、航空航天、半导体制造等特殊领域具有广泛的应用前景［1－5］。

无轴承永磁同步电机转子的稳定悬浮是悬浮力绕组和转矩绕组产生的两种气隙磁场相互作用的结果［6－8］，无轴承永磁同步电机电磁转矩和径向悬浮力之间，以及水平、垂直方向径向悬浮力之间存在着十分复杂的耦合关系，所以要实现无轴承永磁同步电机高性能稳定悬浮运行，必须对其径向悬浮力进行非线性动态解耦控制。

近年来，有学者将神经网络的非线性逼近能力与逆系统方法的解耦线性化能力相结合，提出了非线性系统的神经网络逆控制方法［9］，其基本思想是用静态神经网络逼近非线性函数关系，用积分器表征逆系统的动态特性，由此构成动态神经网络，能完整实现逆系统的静态与动态特性，具有结构简单、易于工程实现等优点，在多变量、非线性耦合系统的线性化解耦控制方面显示了很大的优越性［10－12］。本文在建立无轴承永磁同步电机的悬浮力模型的基础上，分析系统可逆性，构建神经网络逆系统，将神经网络逆系统串在原系统之前构成伪线性系统，并设计闭环PID控制器，实现对无轴承永磁同步电机悬浮力系统的非线性多变量解耦控制。利用Matlab软件环境，构建仿真系统，并进行仿真研究和性能分析。

1 无轴承永磁同步电机的工作原理和径向悬浮力数学模型

1.1 无轴承永磁同步电机的工作原理

无轴承永磁同步电机定子槽中复合叠绕着两套不同极对数的绕组，其中极对数为P1的绕组用来产生电磁转矩（与传统的永磁同步电机定子绕组功能相同），称之为转矩绕组;极对数为P2的绕组用来产生使转子能稳定悬浮的径向悬浮力，称之为悬浮力绕组。当仅有转矩绕组通电时，无轴承永磁同步电机相当于一台传统的永磁同步电机。当悬浮力绕组通电产生的旋转气隙磁场和转矩绕组产生的气隙磁场（包括永磁体产生的气隙磁场）满足以下条件:1）转矩绕组极对数与悬浮力绕组极对数相差1，即P1=P2±1;2）两个磁场的旋转方向一致;3）两套绕组中产生气隙磁场的电流的频率相同，即ω1=ω2。此时，转矩绕组气隙磁场与悬浮力绕组气隙磁场相互作用使无轴承永磁同步电机的转子稳定悬浮和运转［13－14］。

1.2 径向悬浮力产生原理及其数学模型

不考虑转子偏心时，无轴承永磁同步电机的径向悬浮力由麦克斯韦力和洛伦兹力组成。引入悬浮力绕组之后，电机原有的平衡旋转磁场被打破，使得气隙磁场的某一区域增强，而对称区域减弱，因此产生的麦克斯韦力指向磁场增强的一方。两个磁场之间的相互作用如图1所示，其中P1=1，P2=2。图1（a）中，在转子右侧的气隙中，二极转矩磁场与四极悬浮力磁场方向相同，磁场相互叠加，使得右侧气隙内的磁场增强;而在左侧的气隙中，二极转矩磁场与四极悬浮力磁场方向相反，叠加的结果使得左侧气隙中的磁场减弱，故麦克斯韦力的合力指向转子右侧（α正方向）。图1（b）中，在转子上方的气隙中，二极转矩磁场增强了四极悬浮力磁场，使得转子上方气隙中的磁场增强，而转子下方的磁场减弱，因此麦克斯韦合力指向转子上方（β正方向）。

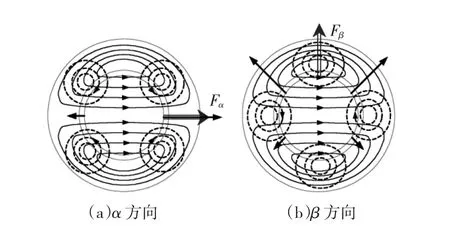
图1 麦克斯韦径向悬浮力产生的原理Fig．1 Principle of Maxwell radial suspension forces generation

由于无轴承永磁同步电机气隙内存在着转矩绕组气隙磁场与悬浮力绕组气隙磁场两种极对数不等的磁场，因此，电机内的洛仑兹力包括了4部分，即载流转矩绕组在转矩绕组气隙磁场中受到的洛仑兹力，载流转矩绕组在悬浮力绕组气隙磁场中受到的洛仑兹力，载流悬浮力绕组在转矩绕组气隙磁场中受到的洛仑兹力与载流悬浮力绕组在悬浮力绕组气隙磁场中受到的洛仑兹力。其中，第一部分洛仑兹力与第四部分洛仑兹力产生了电机的电磁转矩，而第二部分洛仑兹力与第三部分洛仑兹力产生了径向力。当P1=1，P2=2时，无轴承永磁同步电机中载流悬浮力绕组在转矩绕组气隙磁场中受到的α正方向和β正方向的洛伦兹力的情形如图2所示。

图2 洛伦兹径向悬浮力产生的原理Fig．2 Principle of Lorentz radial suspension forces generation

当极对数满足P2=P1+1时，无轴承永磁同步电机中的洛伦兹力和麦克斯韦力方向是一致的，所以径向悬浮力是两者之和;当P2=P1－1时，这两个力是相反的，转子所受合力为麦克斯韦力减去洛伦兹力。本文中P1=1，P2=2，满足第一种情况。无轴承永磁同步电机在d-q轴旋转坐标系下，磁链和电流可以用d-q轴的各分量表示。当悬浮力绕组通电时，无轴承永磁同步电机所受的径向悬浮力可以表示为

此外，由电磁场理论可知，当电机定转子发生偏心时，转子还将受到和偏心位移成正比关系的麦克斯韦径向悬浮力 fα、fβ，他们是一种固有的力，通常称为外界力，其表达式为

式中:k为径向位移刚度;α、β分别为转子在水平、垂直方向的径向位移。

由运动方程可得径向悬浮力的控制模型为

2 径向悬浮力模型的可逆性分析

在对模型进行可逆性分析之前，需要对输出方程求导，直至输出方程中显含有输入变量。根据式（5）可得

3 无轴承永磁同步电机径向悬浮力的神经网络逆解耦控制

由于无轴承永磁同步电机是一个多变量、非线性、强耦合的输入输出系统，其模型非常复杂，径向悬浮力与电磁转矩，以及水平和垂直方向上的径向悬浮力之间存在着强烈的耦合关系。如果不采取有效的解耦措施，无轴承永磁同步电机将不可能稳定悬浮运行，因此实现无轴承永磁同步电机径向悬浮力之间的解耦是保证无轴承永磁同步电机稳定悬浮运行的基本前提。由于无轴承永磁同步电机径向悬浮力的数学模型非常复杂，无法表示成仿射非线系统的形式，同时严格求其逆系统的解析表达式是很困难的，再加上模型的不确定性和参数的时变性，使得反馈线性化方法应用于该系统还有一定的困难。

本文利用静态神经网络和若干积分器s－1来构造无轴承永磁同步电机径向悬浮力模型的神经网络逆，在此基础上，调整静态神经网络的权系数使得神经网络逼近被控对象的逆模型;然后将神经网络逆置于原系统之前，神经网络逆与原系统组成伪线性系统，其输入输出关系是线性的、解耦的。即通过构造神经网络逆系统来“抵消”被控系统的非线性特性，从而实现被控非线性、强耦合系统的线性化和解耦。伪线性系统如图3所示，由神经网络逆和无轴承永磁同步电机径向力模型组成的伪线性系统等效为两个解耦的积分型线性子系统。

图3 伪线性系统Fig．3 The pseudo linear system

对由神经网络逆与无轴承永磁同步电机径向悬浮力模型串联得到的伪线性系统，必须设计线性闭环控制器来实现更好的控制。线性闭环控制器可以采用针对单变量的线性系统理论中的极点配置、PID控制或者二次型指标最优等控制方法。本文选用PD调节器G（s）=1 050+50s作为径向位置调节器。神经网络逆系统与线性闭环控制器组成了神经网络逆控制器，图4为无轴承永磁同步电机径向悬浮力系统的神经网络逆解耦控制结构，右边的虚线框表示为神经网络逆系统，其中静态神经网络用来逼近式（8）逆系统的非线性映射，4个积分器s－1用于表示逆系统的动态特性。

用于逼近逆系统的非线性映射的神经网络可采用任意一种静态神经网络。本文静态神经网络采用3层前馈网络，其中输入层节点数为6，隐含层节点数为14，输出层节点数为2。输出层由具有线性阈值激励函数的神经元组成，隐含层神经元激活函数为

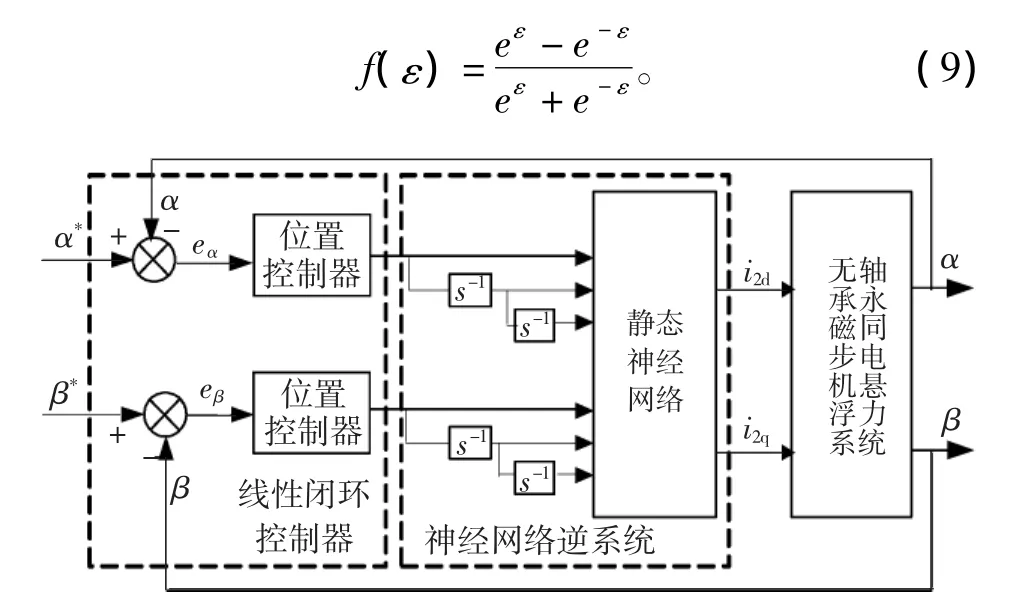
图4 径向悬浮力的神经网络逆解耦控制结构图Fig．4 Decoupling control configuration diagram of radial suspending forces with NNI

根据神经网络逆系统控制方法的步骤，首先需要获取神经网络的训练数据样本，然后再对神经网络进行训练，训练样本集为{，α，β}和{i2d，i2q}，前者为神经网络的输入，后者为期望输出。由于神经网络具有较强的泛化能力，所以其对于未用于训练的样本集中的输入也能给出比较合适的输出，故具有强容错性和鲁棒性。静态神经网络的权系数将在下一步的离线学习中确定。

4 仿真研究

以一台表贴式无轴承永磁同步电机为研究对象，通过仿真研究进一步验证本文提出的解耦控制策略。样机参数为:转矩绕组匝数为240;悬浮力绕组匝数为480;功率为1 kW;电机气隙为2 mm;辅助机械轴承气隙为0.5 mm;转子质量为1 kg;电阻为2.01 Ω;直轴和交轴电感为0.008 H;转子转动惯量为5.6×10－4kg·m2;永磁体等效励磁磁链为0.185 Wb。

4.1 训练样本的获取

考虑无轴承永磁同步电机的实际工作情况，由于无轴承永磁同步电机开环运行时是不稳定的，所以采用闭环控制，以实际运行范围内的随机信号作为闭环系统的输入，以该系统的径向位移作为输出。对无轴承永磁同步电机的两路电流信号（系统输入）和两个方向的径向位移（系统输出）进行采样，整个激励时间设为5.5 s，采样步长取为0.001 s，一共获得5 500组数据，从中等间隔地选取3 000组作为神经网络的训练数据，剩余2 500组作为检验数据，图5为系统的训练样本图。利用高精确度的七点数值算法离线求得径向位移的一阶、二阶导数，从而构成训练样本集{α，β}和{i2d，i2q}。由于神经网络的输入信号大小相差悬殊，这会影响权值学习算法的收敛速度及训练精确度，并会削弱辨识出的神经网络逆系统的泛化能力和鲁棒性。因此将输入及输出信号进行归一化处理，将神经网络的输入输出训练数据转换到［－1，1］范围内。

图5 系统的神经网络逆的训练信号Fig．5 Training signals for NNI of system

4.2 神经网络的离线训练

根据采样得到的输入输出样本集训练神经网络，利用带动量项和变学习率的误差反向传播（back propagation，BP）算法对静态神经网络进行训练，经过1 000次左右训练，神经网络输出均方误差小于0.001，满足要求，从而确定了静态神经网络的各个权系数和阈值。

4.3 神经网络逆解耦控制效果

在仿真研究中，为验证本文所提方法的有效性，需对解耦线性化的结果进行仿真验证，系统的给定输入在不同的时刻发生变化，解耦控制结果如图6所示。t=1.2 s时，径向α轴位移给定从－0.010 mm变化到0.010 mm;t=0.8 s时，径向β轴位移给定从0.020 mm变化到－0.005 mm。由图6可知，控制一个输入只影响一个方向的输出，表明系统实现了α、β方向解耦。

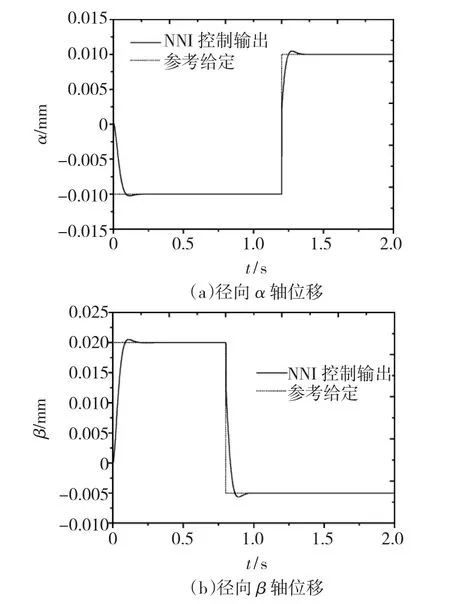
图6 神经网络逆解耦控制结果Fig．6 Results of NNI decoupling control

为了进一步验证神经网络逆系统解耦控制的抗干扰能力，分别在t=0.5 s和t=1.5 s时突加α、β轴方向，大小为15 N的扰动。图7为扰动下的α、β轴的径向位移，可以看出，两位移曲线在小范围内产生了一点波动，但是立刻回到稳定位置，体现了系统具有很好的鲁棒性。

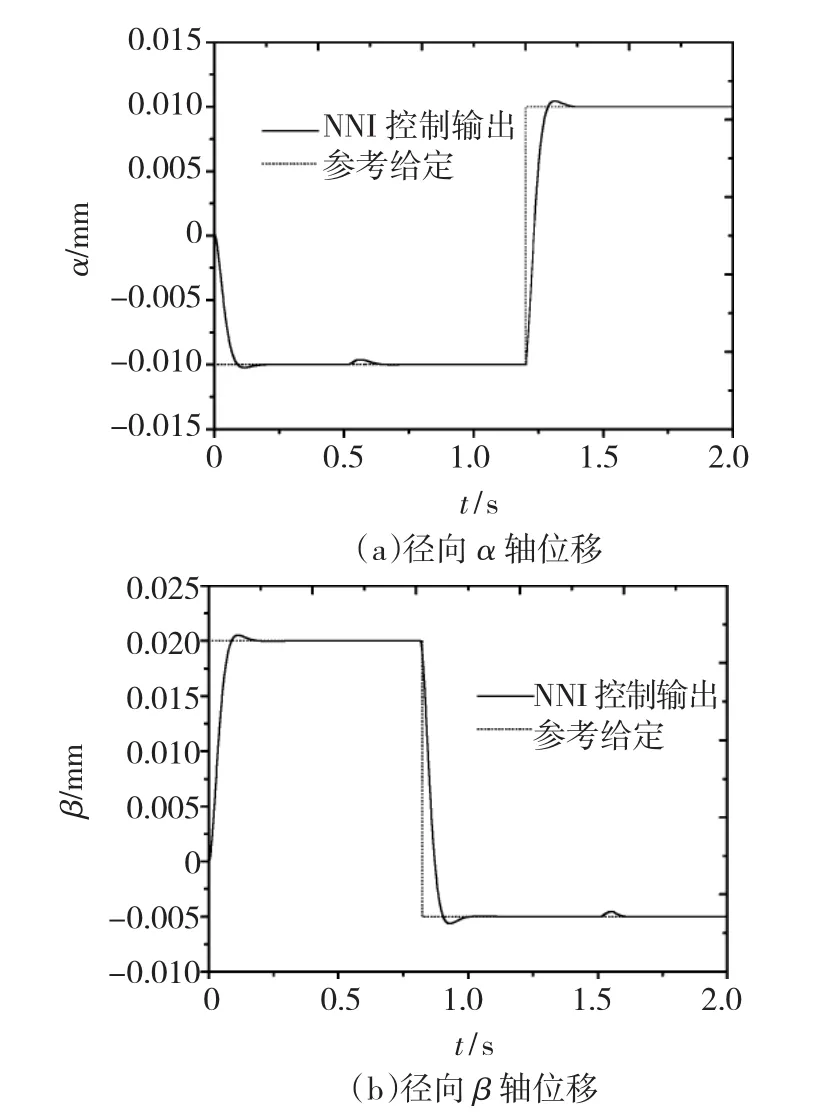
图7 扰动时神经网络逆解耦控制结果Fig．7 Results of NNI decoupling control with disturb

5 结语

本文在介绍无轴承永磁同步电机工作原理的基础上，导出了无轴承永磁同步电机径向悬浮力的数学模型，分析了该模型的可逆性，证明了该系统的可逆性，并应用神经网络逆系统方法成功地实现了无轴承永磁同步电机径向悬浮力之间的动态解耦。利用线性系统的综合方法对解耦后的位置子系统设计调节器进行闭环控制，使系统具有优良的静、动态性能和很强的鲁棒性。仿真结果证明了该控制算法的有效性，为下一步无轴承电机径向悬浮力和电磁转矩的解耦控制及电机带不同负载的研究奠定了一定基础。

［1］朱熀秋，吴熙，陆静，等．一种三相交流混合磁轴承数学模型与性能分析［J］．电机与控制学报，2009，13（2）:245 －250．

ZHU Huangqiu，WU Xi，LU Jing，et al．Mathematics model and performance analysis for a 3-phase AC hybrid magnetic bearings［J］．Electric Machines and Control，2009，13（2）:245 －250．

［2］诸德宏，洪益州，朱熀秋．基于α逆系统理论磁轴承数学模型及控制系统［J］．电机与控制学报，2009，13（4）:497－502．

ZHU Dehong，HONG Yizhou，ZHU Huangqiu．Mathematical model and control of magnetic bearings based on α-th order inverse system theory［J］．Electric Machines and Control，2009，13（4）:497－502．

［3］FANG Jiancheng，SUN Jinji，LIU Hu，et al．A novel 3-DOF axial hybrid magnetic bearing［J］．IEEE Transactions on Magnetics，2010，46（12）:4034－4045．

［4］刘贤兴，孙宇新，朱熀秋，等．无轴承永磁同步电动机的发展、应用和前景［J］．中国机械工程，2004，15（17）:1594－1597．

LIU Xianxing，SUN Yuxin，ZHU Huangqiu，et al．Development，application and prospect of bearingless permanent magnet-type motors［J］．China Mechanical Engineering，2004，15（17）:1594 －1597．

［5］ZHANG Shaoru，LUO Fanglin．Direct control of radial displacement for bearingless permanent-magnet-type synchronous motors［J］．IEEE Transactions on Industrial Electronics，2009，56（2）:542－552．

［6］ZHU Huangqiu，CHENG Qiuliang．Bearingless motor’s radial suspension force control based on flux equivalent with virtual winding current analysis method［J］．Chinese Science Bulletin，2009，54（9）:1590－1598．

［7］ZHU Huangqiu，CHENG Qiuliang，WANG Chengbo．Modeling of bearingless permanent magnet synchronous motor based on mechanical to electrical coordinates transformation［J］．Science in China，Series E:Technological Sciences，2009，52（12）:3736－3744．

［8］SUN Xiaodong，ZHU Huangqiu，PAN Wei．Decoupling control of bearingless permanent magnet-type synchronous motor using artificial neural networks-based inverse system method［J］．International Journal of Modelling，Identification and Control，2009，8（2）:114－121．

［9］戴先中，刘国海．两变频调速电机系统的神经网络逆同步控制［J］．自动化学报，2005，31（6）:890 －900．

DAI Xianzhong，LIU Guohai．Neural network inverse synchronous control of two－motor variable frequency speed-regulating system［J］．Acta Automatica Sinica，2005，31（6）:890－900．

［10］王新，戴先中．一种基于神经网络逆的感应电动机解耦线性化改进策略［J］．电工技术学报，2008，23（4）:32 －38．

WANG Xin，DAI Xianzhong．An improving method to decoupling and linearization of induction motor based on neural network inverse［J］．Transactions of China Electrotechnical Society，2008，23（4）:32－38．

［11］孙玉坤，任元，黄永红．磁悬浮开关磁阻电机悬浮力与旋转力的神经网络逆解耦控制［J］．中国电机工程学报，2008，28（9）:81－85．

SUN Yukun，REN Yuan，HUANG Yonghong．Decoupling control between radial force and torque of bearingless switched reluctance motors based on neural network inverse system method［J］．Proceedings of the CSEE，2008，28（9）:81－85．

［12］刘国海，薛剑锋，康梅，等．两电机调速系统神经网络广义逆在线调整控［J］．电机与控制学报，2009，13（4）:511－515．

LIU Guohai，XUE Jianfeng，KANG Mei，et al．On-line adjustment control of two motor speed-regulating system based on neural network generalized inverse［J］．Electric Machines and Control，2009，13（4）:511－515．

［13］ASAMA Junichi，ASAMI Tetsuro，IMAKAWA Takashi，et al．Effects of permanent-magnet passive magnetic bearing on a twoaxis actively regulated low-speed bearingless motor［J］．IEEE Transactions on Energy Conversion，2011，26（1）:46－54．

［14］OOSHIMA Masahide，TAKEUCHI Chiharu．Magnetic suspension performance of a bearingless brushless DC motor for small liquid pumps［J］．IEEE Transactions on Industry Applications，2011，47（1）:72－78．

（编辑:于双）