巧用必要条件 突破解题难点

●蒋惠光 胡文婷 (奉贤中学 上海 201400)

巧用必要条件 突破解题难点

●蒋惠光 胡文婷 (奉贤中学 上海 201400)

上海市高中一年级第一学期数学教材(试用本)第23页给出了一个关于“子集与推出关系”的定理:“设A，B是2个非空集合，A={a|a具有性质α}，B={b|b具有性质β}，则A⊆B与α⇒β等价”．这个定理告诉我们:“若β是α的必要条件，则A⊆B”．利用必要条件与集合之间的这种关系，常常能够帮助我们在面对一些比较复杂、抽象的数学问题时，巧妙地化解难点，找到解题的突破口．本文将通过对几个典型问题的剖析，阐述在有关问题中利用必要条件解题的一些常用方法和技巧．

1 题设条件特殊化——探求目标所在

都成立，这是一个具有一般性的结论，蕴含着特殊情形．充分利用“若等式对一切正整数都成立，则当n=1，2，3时等式必成立”这一逻辑关系，即“等式对一切正整数n都成立”的必要条件是“当n=1，2，3时等式成立”，由此得到一个方程组，顺利地求出了a，b，c的可能值，后面用数学归纳法证明就水到渠成了．通常，一个具有一般性的结论在某些特殊情形下会变得比较简单，原来难觅踪影的目标往往在特殊情形下就会暴露出它的“原形”，从而为后续的解题打开了“突破口”，这种“从一般到特殊”的思路是一种常用的解题方法．

2 题设条件宽泛化——锁定目标范围

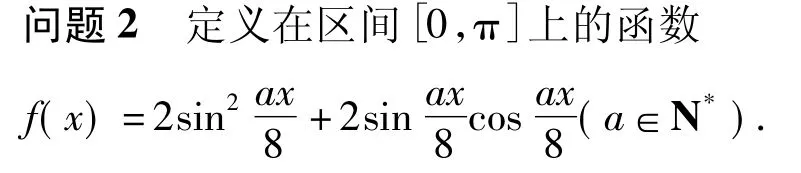
(1)将 f(x)化为 Asin(ωx+φ)+B(其中 A＞0，ω＞0)的形式;

用同样的方法进行验证可知a=4，5，6都满足题设，但a=7不满足．

综上所述，a 的取值为3，4，5，6．

3 题设条件具体化——揭示目标性质

评析本题的难点在于题设条件“a1a2…an=a1+a2+…+an”是一个含有n个未知量的不定方程，比较抽象，难以直接上手．此时需要设法变更条件，使之更加具体、具有“可操作性”．为此，从题设条件推出所求目标 a1，a2，…，an满足性质“a1·a2·…·an－1＜n”和“n＞(n－1)!”(n≥4)，也就是说这2个不等式成立是题设成立的必要不充分条件．由于这2个不等式与n建立了直接而具体的联系，使我们能够从中推出当n≥4时问题无解，并求出了唯一解．这种将原来比较抽象的题设条件具体化的方法是一条重要的解题途径．

4 题设条件简单化——分步逼近目标

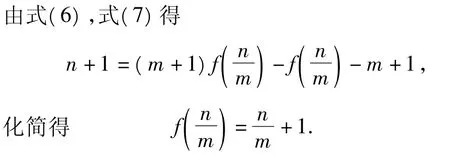
由此可知所求的函数是唯一的，即f(x)=x+1，x∈Q．经检验知，它满足题设条件(1)和(2)．

评析这是一道国际数学奥林匹克竞赛试题，有相当的难度，要想一步到位直接求出满足题设条件的函数f(x)绝非易事．先简单后复杂、从低级到高级，这是我们普遍遵循的一种思维方式．本题从题设所包含的最简单情形开始研究:当y=1时，容易推出结论:f(x+1)=f(x)+1;利用这一递推关系式可得到f(x+n)=f(x)+n和f(n+1)=n+2，这就把结论推广到了整数的情形;再进一步，利用有理数都可以表示为(m，n∈Z，且 m≠0)的形式，运用已得到的结论推出=+1，从而求得函数．

总之，利用必要条件解题是一种“以退为进”的解题策略，其关键在于设计一个恰当的“必要条件”，使之比原来的题设条件具有更强的“可操作性”，更容易入手，从此打开解题的突破口．这种方法对于不少较有难度的数学问题，尤其是对“求满足某种性质的元素或探索其是否存在”这一类数学问题往往是非常有效的!同时，运用此法解题还有利于学生深刻理解充分条件、必要条件和充要条件等重要数学概念，真正弄清它们之间的逻辑关系．这对于培养学生的发散思维、收敛思维能力，形成思维的多样性，提升思维品质都有很好的帮助，值得在日常的教学活动中加以充分利用．

［1］ 蒋惠光．一道自主招生试题的拓展与研究［J］．数学教学，2010(8):41．

［2］ 殷启正，陈志友．国际数学奥林匹克(IMO)思想方法［M］．济南:山东教育出版社，1993．