在活动中感悟数学:以多边形内角和的教学为例

●郜青林 (温岭市第九中学 浙江温岭 317520)

在活动中感悟数学:以多边形内角和的教学为例

●郜青林 (温岭市第九中学 浙江温岭 317520)

《义务教育阶段数学课程标准(修订稿)》强调:学生学习应当是一个生动活泼的、主动的和富有个性的过程．除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式．学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程．在这样的数学活动中，让学生经历从不同角度寻求分析问题和解决问题的方法的过程，体验解决问题方法的多样性，掌握分析问题和解决问题的一些基本方法．并在与他人合作和交流过程中，更好地理解他人的思考方法和结论．下面笔者结合《多边形内角和》的教学设计，例谈如何组织开展数学活动．

1 基于学生的知识基础，提出活动问题

重视研究学生原有的知识基础．任何新知识都是旧知识的延伸发展，因此教师要认真深入研究学生学习新知识所必备的知识基础及旧知识的掌握状况．即已经知道什么，哪些知识掌握得较扎实，哪些知识掌握得较模糊等，从而确定教学的途径、方法．因为学生在小学阶段已经初步掌握了三角形的内角和及正方形和长方形的内角和等知识，所以笔者在“多边形内角和”的教学导入是这样设计的:

师:大家还记得三角形的内角和是多少度?

生:180°．

师:正方形、长方形的内角和呢?

生:360°．

师:任意一个四边形的内角和是否也是360°?

生:……(给学生1分钟左右的时间思考)．

设计意图从学生的实际出发，开门见山地谈到了本节课需要的知识基础“三角形的内角和”，同时也给学生留下了思维的空间．既重视全体学生的学情，又重视个别学生的学情，有利于因材施教．

2 利用学生的已有经验，探究新知识

孔子曾说过:“不愤不启，不徘不发”．教师作为一个启发者、引导者，应为学生根据所学知识巧妙设计问题，使学生产生“心欲求而未得，口欲言而不能”的积极进取状态，让学生达到“愤悱状态”．激发学生的求知欲，调动学生积极主动地探索、分析、解决问题．可采用多种方式引导探索，让学生先通过尝试、探索思考，然后讲解引导获得新知识;或先猜后证，即学生先通过大胆猜想发现结论，然后教师引导证明;亦或学生先动手实验，进行观察、分析从而发现规律，然后教师引导寻求结论．在此过程中，教师要适时点拨充分发挥主导作用．在抛出问题“任意一个四边形的内角和是否也是360°”后，可以进行如下引导:

师:(点拨)大家能利用三角形内角和去研究四边形的内角和等于360°吗?

生:……(给学生1分钟左右的时间思考)．

师:(点拨)用三角形的知识去证明四边形的知识，关键是什么?

生:只要将四边形分成几个三角形即可．

师:请同学自己动手试试，分好后再简易推理四边形的内角和是不是360°．

(分小组，放手由学生自己去实践，教师掌握各组的进程，并作指导．)

展示学生的几种方案如下:

生1:连结一条对角线，如图1所示．把四边形分成2个三角形，四边形 ABCD的内角和等于△ABD的内角和与△BCD的内角和之和，即180°+180°=360°．

图1

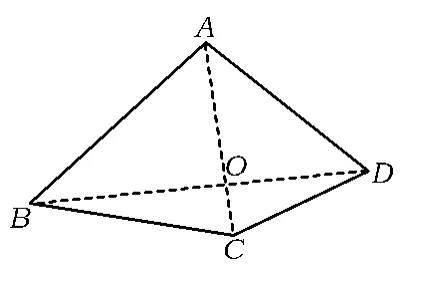
图2

生2:连结2条对角线，如图2所示．把四边形分成4个三角形，则四边形ABCD的内角和等于△ABO，△BCO，△DCO，△ADO的内角和之和减去360°，即180°+180°+180°+180°－360°=360°．

(教师提出:若点O不是对角线的交点，则可以吗?点O在边上或在四边形的外部，又如何推理呢?如图3，推理过程此处略．)

图3

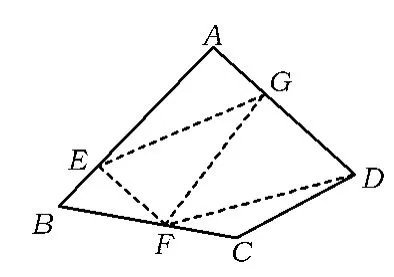
图4

生3:不考虑交点的位置也可以证明．如图4所示，四边形ABCD的内角和=△AEG的内角和+△EBF的内角和+△EFG的内角和+△FDG的内角和+△FCD的内角和－180°－180°－180°=180°+180°+180°+180°+180°－180°－180°－180°=360°．

设计意图该设计注重培养学生的能力，同时也体现了教师的主导作用．以学生为本，把课堂还给了学生．只有这样，学生的头脑才真正动起来，才能真正地参与到知识的发现过程中来，我们的教学才能真正做到注重过程而不是结论．

3 引导学生归纳活动过程，拓展知识

通过对任意四边形内角和的探究，学生已经找到了研究多边形内角和的最简单办法．教师应该趁热打铁，帮助学生总结方法并加以拓展，可以作如下设计:

师:大家分得很好，这说明用三角形的知识去研究四边形的方向是正确的，也足以说明任何四边形的内角和都是360°．大家回顾一下刚才的作图，哪种分法及推理更简洁呢?

生:生1的分法更简洁．

师:生1的作法就是从一个顶点引对角线，从而分成了2个三角形．那么大家考虑:从五边形的一个顶点出发，可以引几条对角线?它们将五边形分为几个三角形?五边形的内角和等于180°乘以几?

同时，在屏幕上打出从五边形一个顶点出发，可以引＿＿条对角线，它们将五边形分为＿＿个三角形，五边形的内角和等于180°×＿＿ ．．

生:2条对角线，3个三角形，乘以3．

师:请大家完成屏幕上的表格，如表1所示．

表1 对角线数、三角形数与内角和

师:从表格上你发现什么规律?

生:从一个顶点画的对角线的条数比边数少3，分成三角形的个数比边数少2．

师:为什么会这样呢，是不是任意多边形都有这个规律，能推理吗?

生:在画对角线时，不能往点的自身及和它相邻的2个点引，故此比边数少3;而除与这个顶点相邻的2个边外的边都对应一个由对角线分这个顶点而成的角，刚好有边数少2个三角形．

师:你观察得很仔细，那么大家可以说出100边形的相应数值吗?

生:97条，98个三角形，内角和为98乘以180°．

师:那n边形呢?

生:(n－3)条，(n－2)个三角形，内角和为(n－2) ×180°．

师:大家通过学习得到了多边形的内角和为(n－2)×180°，其中n表示的是什么?

生:边数．

师:对，n表示多边形的边的条数．在研究一个复杂问题时，通常可以转化为从简单问题入手来研究，去寻求规律，从而使复杂问题得以解决．

设计意图通过由一个顶点出发引多边形的对角线是分割多边形为三角形，探求多边形内角和的最简单方法入手，是研究问题的一般规律，也是探求复杂问题结论的一种方法，潜移默化地培养了学生解决问题的能力．

从三角形的内角和到多边形的内角和，在教学中通过分图活动以及师生的共同探究，让学生感受一种研究问题的一般方法，从特殊到一般的经历，体会数学的转化思想．因此，在教学时，教师一定要掌握知识发生的渊源，尽可能地给学生创造数学活动的机会，培养他们探究的习惯．其实，只要我们在教学活动上多花点功夫，经常反思活动成效，让学生在课堂上体验做数学的乐趣，品尝做数学的快乐，课堂教学就一定能高效率地开展起来，也能得到更好的教学效果，从而实现轻负高质的愿望．