一种四自由度空间并联机构的奇异容错纠错策略与方法研究

陈 斯 范守文

电子科技大学，成都，611731

一种四自由度空间并联机构的奇异容错纠错策略与方法研究

陈 斯 范守文

电子科技大学，成都，611731

以Gosselin的奇异分类为基础，将第二类奇异位形对并联机构的不利影响看成是一种机械系统故障，提出了结合冗余驱动的并联机构奇异容错纠错策略框架。阐述了该容错纠错策略框架的基本思想和实现步骤，用线性方程组解的情况和矩阵条件数解释了该奇异位形“故障”发生和被克服的实质，以此为基础定义了描述奇异被消除程度的奇异容错度指标，基于该指标提出了容错结构优化算法，用来确定使并联机构具有最佳奇异容错能力的冗余驱动的结构参数。分析得到了2RPS＆2TPS型并联机构的一个典型的第二类奇异位形，比较了三种奇异容错策略克服这一奇异位形效果的优劣，对这三种容错纠错策略进行了仿真研究，结果表明，提出的以奇异容错度为依据的容错纠错策略能有效克服奇异位形的不良影响。

并联机构；奇异位形；容错；纠错；冗余驱动

0 引言

容错纠错技术是提高机电产品可靠性的有效手段［1］。现代机电产品正朝着集成化、自动化、智能化的方向发展，其发生故障的随机性很大，往往难以预料。工程实践表明，除了少数突发故障以外，大多数故障如果早期发现，及时采取恰当的措施是完全可以防止的。虽然人们无法保证所设计的系统各个构成环节绝对可靠，但如果将容错、纠错的概念引入到系统中，构成容错、纠错系统，则可以使系统中的各个故障因素对系统性能的影响被显著削弱，这就意味着间接地提高了系统的可靠性，尤其是在构成系统的各个部件的可靠度未知时，容错、纠错技术更是在系统设计阶段保证了系统可靠性的要求，为提高复杂系统的可靠性开辟了一条新途径。容错纠错的基本思想是：在系统中存在一定的冗余，容错技术能够自动适时地监测并诊断出系统的故障，然后采取相应的控制方案或处理方法自动隔离或在线修复故障［2］。

机构的奇异位形可以定义为机构运动状态不可控的点的集合。并联机构由于其具有特殊的闭环结构，所以比其他类型的机构拥有更多的奇异区间、更丰富的奇异种类，理论分析也更加复杂［3－5］。奇异位形对并联机构的有效工作空间、可控性、刚度、速度变化的均匀性和运动的灵活性等都会产生不利的影响［6－7］。

并联机构的奇异位形可以看作先天固有的一类机械系统故障。机构如果对“奇异”这种“故障”具备了容错纠错能力，它的应用价值将得到进一步的提高。文献［8］从理论上证明了冗余驱动能够消除驱动奇异，文献［9－11］就不同的并联机构提出了冗余驱动的实现方法并取得了较好的效果。

本文提出了并联机构奇异位形容错纠错策略的基本框架，基于线性方程组解的分类和矩阵条件数的数学意义给出了添加冗余驱动不产生额外内力的条件、冗余驱动克服第二类奇异的判定依据以及奇异容错失效的原因，最后围绕克服2RPS＆2TPS型并联机构一个典型的奇异位姿问题，对并联机构奇异容错能力的评价指标、冗余驱动结构参数的最优设计和各种奇异容错策略的优劣比较进行了讨论。

1 并联机构的奇异容错纠错策略

2RPS＆2TPS型并联机构如图1所示，它由正方形布局、外接圆半径分别为r和R的动平台和固定平台，以及连接它们的4条腿组成，4条腿的长度分别为l1、l2、l3、l4，4条腿与动平台由球铰连接。l1、l3与定平台由轴线与B2B4平行的转动副连接，l2、l4与定平台由虎克铰或球铰相连。机构的自由度为4，每条腿中各有一个移动副，在4条腿驱动器的作用下，动平台可以实现空间的位置和姿态变化。

图1 四自由度空间并联机构简图

并联机构奇异的实质是机构的雅克比矩阵降秩，位形空间与驱动空间因失去确定的映射关系而处于不可控的状态。并联机构奇异位形的分类方法中经典的有 Gosselin［12］和 Park［13］的分类方法，在Gosselin的奇异分类方法中，第一类、第三类奇异发生在工作空间边界，通过限定驱动器运动范围很容易就能避免；第二类奇异以奇异曲面的形式大量存在于工作空间内部，将工作空间分割成互不连通的区域，机构的结构越复杂，奇异曲面越复杂，对运动影响也越大。第二类奇异发生时，末端执行器具有瞬时自由度，机构在外力的作用下不能保证静态平衡，处于一个不稳定的状态，第二类奇异也称为力不确定位姿或力不约束位姿，克服它的方法最值得研究。本文将第二类奇异看作机械系统的“故障”，研究了其容错纠错技术，下文提到的奇异都是指第二类奇异。

并联机构对奇异的容错纠错是指机构在无人干预的情况下能顺利地度过奇异位姿，完成预定操作任务。基本原理如图2所示。故障检测模块由传感器测得的数据计算得到描述奇异位形可诊断性和可修复性两个指标值。首先比较诊断性指标，当它高于某值时，机构正常工作，冗余驱动器处于从动状态；当它低于某值时，故障发生。再比较修复性指标，当它高于某值时，系统对故障具有容错纠错能力，冗余驱动器启动，添加的冗余驱动的关节由被动变为主动；当它低于某值时，故障不能自动排除，系统停机，报警。

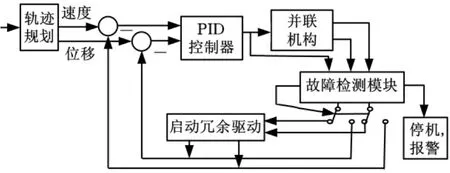
图2 奇异位形容错纠错控制系统原理框图

2 冗余驱动实现奇异容错的原因分析

设驱动器数为m，自由度数为n，A′的秩为R（A′），则A′∈ Rm×n（m ＞n），A 为A′的子方阵。对于某时刻特定的输入，B′q·′ 可看作常量，式（3）为超定线性方程组，它的解分三种情况。

（1）R（A′）＞n时式（3）无解，对应冗余驱动产生很大的内力，机构可能遭到破坏。因此添加冗余驱动的必要条件是R（A′）≤n，即冗余驱动器的运动不任意，应由其他驱动器运动的线性组合给出。后面的讨论只针对R（A′）≤n的情况。

（2）R（A′）＝n时式（3）有唯一解。此时机构可能处于两种状态：一是原机构不发生奇异；二是冗余驱动克服了奇异，方程组必须满足m－n≥n－R（A），且引入冗余驱动而增加的m－n个方程中有n－R（A）个线性无关的方程不能由式（2）中任意r′个方程线性表示。

（3）R（A′）＜n 时式（3）有无穷多解。由于R（A）≤R（A′），故A奇异。该情况发生的原因有二：当m－n＜n－R（A）时，有R（A′）≤R（A）＋（m－n）＜n，实质是添加冗余驱动器的数量不够；当m－n≥n－R（A）时，增加的m－n个方程中找不到n－r′个线性无关的方程或这n－r′个方程中有方程能由式（2）中r′个线性无关的方程线性表示。这两种情况都对应于冗余驱动没有克服奇异。

3 容错性能指标与容错结构优化

国内外学者对冗余驱动克服奇异位形做了一些有价值的研究工作。文献［8］将冗余驱动力能否在机构的不可控运动方向做功作为判定奇异是否得到克服的判定依据，文献［10］以平面三自由度并联机构为例，通过比较添加冗余驱动前后机构所具有的奇异位姿的减少说明冗余驱动克服了奇异。对于冗余驱动的启动控制，需要提出一个指标来定量描述奇异被克服的程度。本文定义了并联机构的奇异位形容错纠错度指标，它只与机构的结构参数、运动位姿和冗余驱动的结构参数有关，以下简称为奇异容错度，用χ表示：

式中，i＝Cnm，m＞n；Aj为机构中n个驱动约束方程构成的方程组的辅助正解雅克比矩阵；cond（）为矩阵的条件数函数；λj为各个雅克比矩阵条件数的权系数，cond（Aj）→ ∞时，λj＝0，否则λj＝1。

特别地，对于没有冗余驱动器工作的原机构，m＝n，将它的奇异容错度记为χ0：原机构在发生奇异的位姿处不具有奇异容错能力，所以这些位姿对应的χ0为零。χ0＝0可以作为原机构发生奇异的判定依据。

矩阵的条件数刻画了扰动对方程组解的影响程度。cond（A）能反映并联机构的三种状态：cond（A）较小时数值稳定性好，对于q·的微小变化，p·的变化也很小，机构的可控性和运动性好；cond（A）较大时数值稳定性差，q·的微小变化能引起p·很大的变化，机构的可控性和运动性差；cond（A）无穷大时A奇异，q·不变时p·仍能在对应特征向量方向上变化，即动平台具有了瞬时自由度，机构发生奇异。cond（A）≥1恒成立，所以0≤χ≤1。当χ＝0时，所有cond（Aj）都为无穷大，即A′中每个n阶子方阵都奇异，R（A′）＜n，冗余驱动没有克服奇异；当χ＞0时，R（A′）＝n，冗余驱动克服了奇异。χ越大说明容错的效果越好。

由以上的分析可知：冗余驱动实现奇异容错的充要条件是，在原机构发生奇异的位姿处冗余机构的奇异容错度大于零，即χ＞χ0＝0。

定义奇异容错度的维数为驱动器数与机构维数之差，简称奇异容错维数，记为V（χ），即

显然V（χ0）＝0。某一奇异具有容错的必要条件是奇异容错维数不小于奇异空间的维数，即

并联机构添加冗余驱动前后的奇异容错度分别为χ和χ0，一方面它们可以分别作为诊断性指标和修复性指标实现容错控制，另一方面也能利用它们对冗余驱动的结构参数进行优化设计。χ描述了奇异被消除的程度，它的大小只与原始机构的结构参数、位姿变量及冗余驱动的结构参数有关。因此容错结构优化问题可以描述为：根据已知的操作任务确定原始机构的结构参数，并由χ0＝0确定出机构发生奇异的位姿后，搜索冗余驱动的结构参数，使χ极大化，即

式中，p为并联机构的位姿输出向量；Rp为运动平台工作空间；e为添加冗余驱动的分支与动平台相连的铰链点在基础坐标系中的坐标向量；Re为e所允许选取的位置的集合；f为添加冗余驱动的分支与定平台相连的铰链点在基础坐标系ξ中的坐标向量；Rf为f所允许选取的位置的集合。

满足式（9）、式（10）的位姿发生了奇异，式（11）是对冗余驱动结构参数的约束。式（7）～式（11）是非线性约束最优化问题。

4 奇异容错纠错实例

4.1 原始机构的奇异位形分析

建立坐标系如图1所示，定平台各铰链点在基础坐标系ξ中的坐标为：Bi＝ （gi，hi，0）T，i＝1，2，3，4。动平台上各铰链点在动坐标系ξ′中的坐标为：P′i＝（mi，ni，0）T，i＝1，2，3，4。

ξ′相对于ξ的姿态可通过两次旋转变换得到：①绕y轴旋转角度α；②绕x′轴（由旋转变换①得到）旋转角度β。旋转变换矩阵R为

4条腿的长度用铰链点Bi、Pi的坐标表示为：｜Bi－Pi｜2＝l2i，得到机构的约束方程如下：

由式（17）知：α＝β＝0时｜A｜＝0，即两平台平行时发生奇异。机构运动通过该位姿时，它的各种性能将难以保证，机构若要在此位姿停留，在外力的作用下将失去平衡。

4.2 容错策略及容错效果分析

添加带驱动的TPS分支是并联机构实现冗余驱动常用的方法，由自由度计算可知，添加这种分支不改变原机构的自由度。用此方法在2RPS＆2TPS机构上实现冗余驱动，该分支安装的位置不同会影响奇异容错的效果。假设它与动平台中心p相连，与定平台的连接点f可以在定平台上任意选取。

方案Ⅰ：f点选为O，如图3a所示。写出约束方程后对时间求导，再与式（15）构成新的方程组，得到此冗余机构的A′1，代入α＝β＝0后经初等行变换得

由式（18）知R（A′1）＜4，说明方案 Ⅰ 没有克服奇异。从上面的过程不难发现，现有的冗余驱动结构参数的设计方法具有一定的盲目性，随意添加冗余甚至有时不能达到奇异容错的效果。

笔者通过研究发现动平台和固定平台上各铰链点的对称分布是造成这一奇异发生的原因，可以采用不规则的铰链点分布消除此类奇异。

方案Ⅱ：如图3b所示。相比原始机构，铰链点B2在基础坐标系中的坐标选取为（－0.5R，－R，0），其他结构参数不变。l2对应的约束方程为

用式（20）替换式（15）中对应的方程后代入α＝β＝0，并经初等行变换得

由式（21）知R（A′2）＝4，所以方案 Ⅱ 克服了这类奇异。

图3 机构简图

4.3 仿真算例及分析

外接圆的半径分别取R＝180mm，r＝90mm，动平台中心p点在基础坐标系ξ中的坐标为（70，0，400）mm，α、β 在 （－10°，10°）范围内变化。用容错结构优化方法进行运算：第一步由式（9）、式（10）得到机构发生奇异的一个姿态参数α＝β＝0。将α＝β＝0代入原机构的辅助正解雅克比矩阵，得到奇异容错维数为1，确定需要添加冗余驱动器最少的数目为1。冗余驱动机构的A′3为

由式（22）可知，f点坐标在Y轴方向的选取对于奇异容错的效果没有影响。确定f点在X轴方向的坐标fX为优化设计变量，由容错结构优化算法求得fX＝±180mm。将f点选为A1点的方案记为方案Ⅲ，如图4所示。

图4 机构简图

图5 奇异容错度随α的变化曲线

图5为β＝0、α∈ （－3°，3°）时，原机构和方案Ⅰ、方案Ⅱ、方案Ⅲ的奇异容错度随α的变化情况。从图5中可看出零维奇异容错度在α＝0°附近急剧地趋向于零，说明原机构在α＝β＝0处发生了奇异；方案Ⅰ的奇异容错度在α＝β＝0处也为零，说明它没有起到克服奇异的作用；方案Ⅱ、方案Ⅲ在α＝β＝0处都不为零，说明它们克服了奇异；方案Ⅲ的奇异容错度值比方案Ⅱ的奇异容错度值大，说明方案Ⅲ的奇异容错效果更好，图6显示了奇异容错度的值与fX之间的关系。

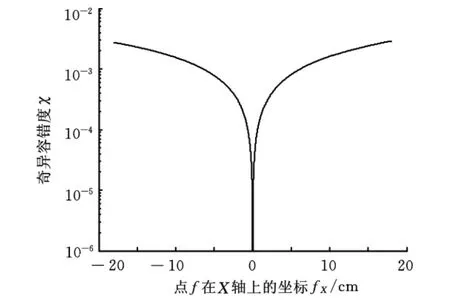
图6 奇异容错度与fX的关系

5 结论

（1）发现了2RPS＆2TPS型并联机构一个典型的奇异位形位姿，当固定平台与动平台平行时，出现奇异位形；证明了采用不规则的铰链点分布能有效消除该奇异位形。

（2）随意添加冗余驱动具有一定的盲目性，有时甚至起不到消除奇异的效果；基于奇异容错度的冗余驱动器结构参数的优化设计方法能够得到奇异容错效果最佳的添加冗余驱动的方案。

（3）当机构一些尺寸参数由于某些原因确定且无法修改时，添加冗余驱动消除奇异的方法相比不规则的铰链点分布法具有更好的奇异容错效果。

［1］ 范守文，黄洪钟，杨玻玻.机电产品的容错纠错设计系统及其基本框架研究［J］.计算机集成制造系统，2007，13（7）：1275－1281.

［2］ Russell K，Sodhi R S.Kinematic Synthesis of Adjustable RRSS Mechanisms for Multi－phase Motion Generation［J］.Mechanism and Machine Theory，2001，36（8）：939－952.

［3］ 黄真，杜雄.3／6－SPS型Stewart机器人的一般线丛奇异分析［J］.中国机械工程，1999，10（9）：997－1000.

［4］ 吴宇列.并联机构奇异位形的微分几何理论以及冗余并联机构的研究［D］.长沙：国防科学技术大学.2001.

［5］ 沈辉，吴学忠，李泽湘.并联机构奇异点的运动分岔研究［J］.国防科技大学学报，2004，26（6）：54－57.

［6］ 韩先国.并联机床相关理论及设计方法研究［D］.北京：北京航空航天大学，2002.

［7］ 李艳文.几类空间并联机器人的奇异研究［D］.秦皇岛：燕山大学，2005.

［8］ 白志富，韩先国，陈五一.冗余驱动消除并联机构奇异研究［J］.航空学报，2006，27（4）：733－736.

［9］ Marquet F，Krut S，Company F，et al.ARCHI：A New Redundant Parallel Mechanism－modeling，Control and First Results［C］／／Proceedings of the 2001IEEE／RSJ International Conference on Intelligent Robot and Systems.Maui，Hawaii，USA，2001：183－188.

［10］ Wang Jinsong，Wu Jun，Li Tiemin，et al.Workspace and Singularity Analysis of a 3－DOF Planar Parallel Manipulator with Actuation Redundancy［J］.Robotica，2009，27：51－57.

［11］ Sadjadian H，Taghirad H D.Kinematic，Singularity and Stiffness Analysis of the Hydraulic Shoulder：A 3－d.o.f.Redundant Parallel Manipulator［J］.Advanced Robotics，2006，20（7）：763－781.

［12］ Gosselin C，Angeles J.Singularity Analysis of Closed－loop Kinematic Chains［J］.IEEE Transaction on Robotics and Automation，1990，6（3）：281－290.

［13］ Park F C，Kim J M.Singularity Analysis of Closed Kinematic Chains［J］.Transactions of the ASME Journal of Mechanical Design，1999，121（1）：32－38.

Study on Fault Tolerance and Fault Rectification Strategy and Approach for Singularities of a 4－DOF Spatial Parallel Mechanism

Chen Si Fan Shouwen
University of Electronic Science and Technology of China，Chengdu，611731

Based on singularity classification approach of Gosselin，singularities of typeⅡ were treated as a kind of mechanical system faults，a fault－tolerance and fault－rectification strategy framework for eliminating singularities was presented based on actuation redundancy herein.Basic idea and implementation process of this framework were expatiated，the essence of singularity occurring and singularity being removed were interpreted by solutions of linear equations and matrix condition number.Degree of singularity fault－tolerance was defined as an index for describing the performance of singularities being eliminated.Based on this index，an optimization algorithm was proposed to determine optimal structural parameters for the redundant actuation，which enabled parallel manipulators to possess maximum singularity fault－tolerance ability.A typical singularity loci for 2RPS＆2TPS parallel mechanism was obtained，three fault－tolerance and fault－rectification strategies were presented and compared in details.Simulation researches for above three fault－tolerance and fault－rectification strategies were conducted.Simulation results show that the fault－tolerance and fault－rectification strategy based on degree of singularity fault－tolerance can eliminate side effect of singularities in parallel mechanisms effectively.

parallel mechanism；singularity；fault－tolerance；fault－rectification；actuation redundancy

TH11；TG502.13

1004—132X（2011）10—1143—06

2010—07—28

国家自然科学基金资助项目（50775027）；机械传动国家重点实验室开放基金资助项目（SKLMT－KFKT－201010）；流体传动及控制国家重点实验室开放基金资助项目（GZKF－201029）

（编辑 袁兴玲）

陈 斯，男，1985年生。电子科技大学机械电子工程学院硕士研究生。主要研究方向为并联机构设计、容错控制。范守文，男，1968年生。电子科技大学机械电子工程学院教授、博士研究生导师。