基于频率加权的整车主动悬架系统控制器降阶研究

黄长喜 汪洪波

合肥工业大学,合肥,230009

基于频率加权的整车主动悬架系统控制器降阶研究

黄长喜 汪洪波

合肥工业大学,合肥,230009

建立了整车7自由度主动悬架系统动力学模型。考虑高频动态未建模不确定性和人体对振动的敏感频段等因素,为有效抑制路面干扰,设计了加权广义悬架系统 H∞控制器。在此基础上,应用频率加权右互质分解控制器降阶方法对所设计的高阶控制器进行降阶。乘坐舒适性比较和频域仿真分析结果表明,高阶控制器的阶数被较大程度地降低,且降阶悬架闭环控制系统能获得与全阶悬架闭环系统相近似的控制性能。

主动悬架;H∞控制;频率加权;控制器降阶

0 引言

近年来,汽车悬架系统的主动控制研究引起了国内外众多学者和研究人员的重视,各种现代控制方法被应用于设计主动悬架控制器,且获得了最优的闭环悬架控制性能[1-3]。然而,由于整车悬架系统数学模型阶次很高,导致所设计的最优控制器、鲁棒控制器等阶次亦较高,使得控制器的工程实现成为难题。为此,寻求尽可能简单的控制器并保证悬架闭环系统具有较好的控制性能,将是众多车辆设计、控制工程师关心的问题。文献[4]通过分析1/4车液压气动的非线性悬架模型的特征获得了包含主导状态的低阶模型;文献[5]将奇异摄动降阶法应用于全车悬架模型的降阶中;文献[6]给出了一种Hankel范数最优降阶方法的算法,并将其应用于半车主动悬架模型的降阶中;文献[7]将基于线性矩阵不等式的控制器降阶方法应用于主动悬架系统中,该方法能保证降阶闭环系统的稳定性和控制性能。

本文首先建立7自由度整车悬架模型,考虑高频动态未建模不确定性和人体对振动的敏感频段,设计了频率加权的广义悬架系统H∞控制器。在此基础上,应用频率加权右互质分解的控制器降阶方法对所设计的高阶控制器模型进行降阶研究,并进行了闭环悬架系统乘坐舒适性比较和频域仿真结果分析。

1 整车7自由度主动悬架系统模型建立

考虑簧载质量的垂向、俯仰、侧倾运动以及非簧载质量的垂向运动,建立的汽车7自由度的整车模型[8-9]如图1所示。

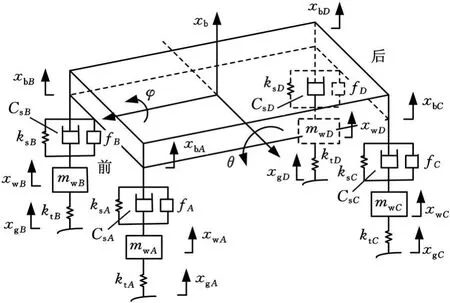
图1 整车7自由度主动悬架系统示意图

在俯仰角θ和侧倾角φ较小时,车身4个端点(A、B、C、D)处的垂直位移有如下关系:

则可得主动悬架系统(ASS)的状态空间模型为

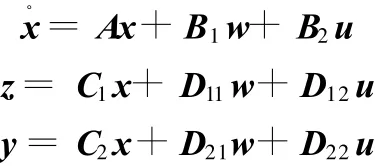
式中,A、B1、B2分别为系统状态矩阵、系统干扰输入矩阵、系统控制输入矩阵;C1、D11、D12分别为被控状态矩阵、被控干扰输入矩阵、被控控制输入矩阵;C2、D21、D22分别为量测状态矩阵、量测干扰输入矩阵、量测控制输入矩阵。

2 H∞控制器设计

对主动悬架被控系统G0设计 H∞输出反馈控制器,其输出反馈闭环控制系统框图见图2。

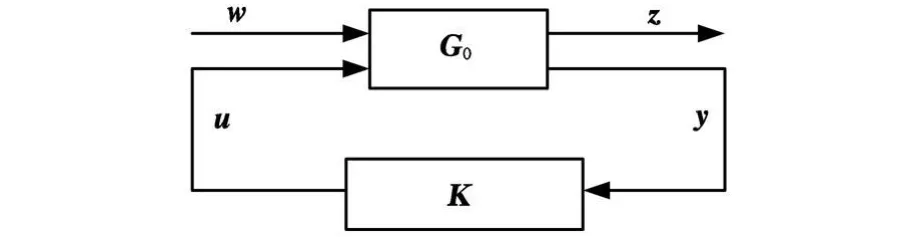
图2 输出反馈控制系统

根据ISO2631-1997标准,人体对振动的敏感频率范围在垂直方向为4～8H z,在旋转方向为1～2H z。取垂直方向和俯仰、侧倾旋转方向加权传递函数[6]分别为

考虑高频动态未建模的不确定性及人体对振动敏感频段的加权传递函数,主动悬架加权广义控制系统框图见图3,图中p、q分别为高频动态未建模不确定性输入量和输出量。其中不确定性由W robΔu 表示 ,其中:经检验,此为28阶稳定的系统模型。

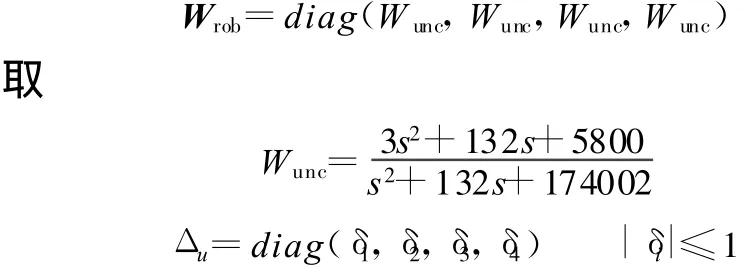
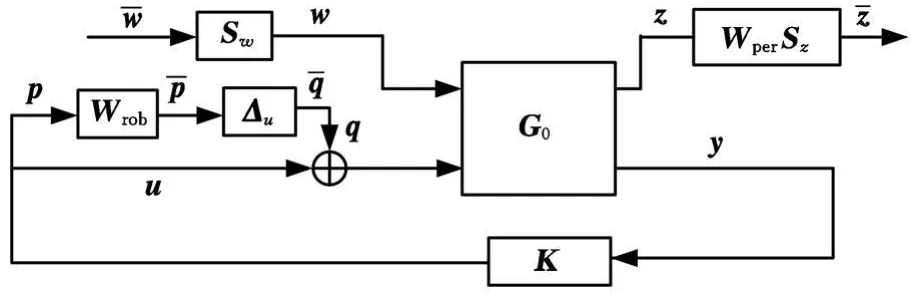
图3 加权广义悬架控制系统框图

根据H∞控制理论,为使干扰输入的影响得到有效抑制,此时控制器的设计问题转化为广义系统的 H∞设计问题,可利用MATLAB/LM I工具箱求解出控制器,以使得

3 基于频率加权右互质分解的悬架控制器降阶研究

根据文献[10],在MATLAB软件中编写频率加权的右互质分解控制器降阶算法程序,对所设计的28阶控制器进行降阶研究。为了评价降阶控制效果,假定汽车以20m/s的速度直线行驶在B级路面上,路面的功率谱密度函数[11]为S(f)=Kroadvs/f2,Kroad=5×10-6m,速度 vs=20m/s,频率 f的单位为Hz。根据ISO2631-1,引入汽车舒适性指标GCI作为评价指标:

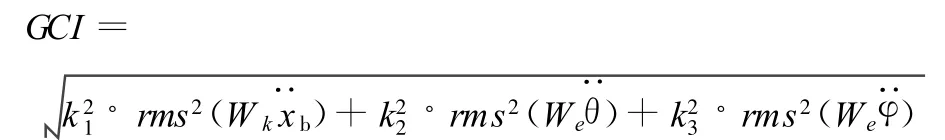
其中取系数k1=1,k2=0.4,k3=0.63,加权传递函数Wk、We的选取参见文献[6],rms为均方根求取函数。器的阶数降至更低时,各项指标相对增大较多,闭环性能损失较多。

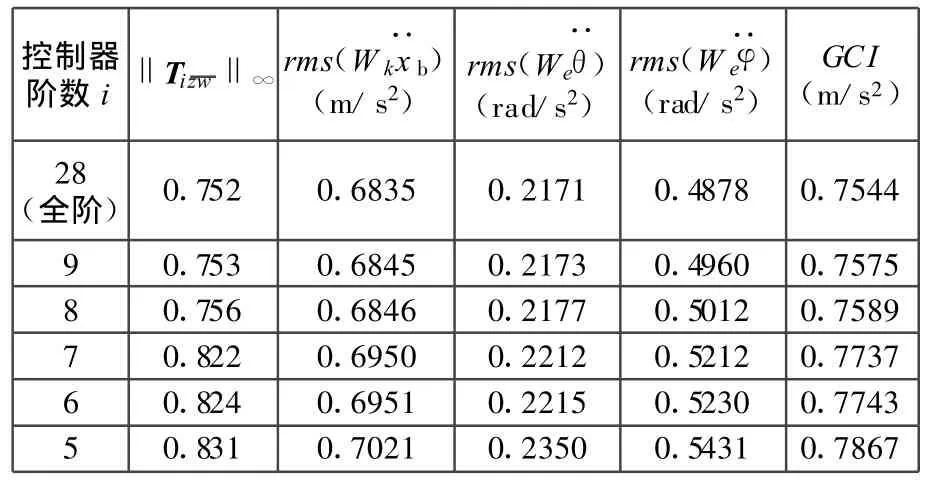
表1 不同阶闭环悬架系统汽车乘坐舒适性比较

因此,为了获得阶数尽可能低的控制器且与全阶控制器相近的控制效果,可将28阶降至8阶较为合适。

4 仿真结果分析

为了更好地观察降阶控制器的闭环控制性能,将全阶、所获得的8阶降阶悬架控制器与考虑高频动态未建模不确定性的原被控对象构成的广义全阶、降阶悬架闭环控制系统(分别记为FASS、RASS)和被动悬架系统(记为PSS)频域响应进行比较,仿真结果如图4～图9所示。图4～图9分别表示从左前路面位移输入xgA分别至车身质心处垂向加速度x¨b、车身俯仰角加速度θ¨、车身侧倾角加速度φ¨、左前悬架动挠度(xbA-xwA)、右前悬架动挠度(xbB-xwB)、左前悬架作动力 fA输出的传递函数的幅频增益,分别记为FG1、FG2 、FG3 、FG4 、FG5 、FG6 。

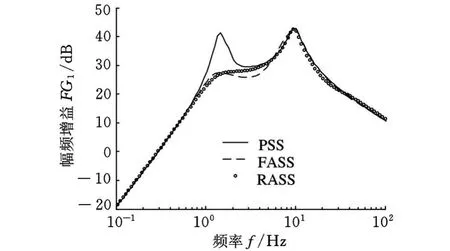
图 4 x gA至x¨b的传递函数的幅频增益

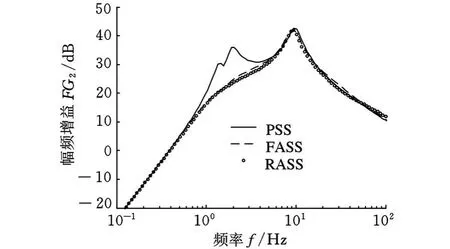
图 5 x gA至θ¨的传递函数的幅频增益

从图 4～图 9所示频域仿真结果可看出,RASS、FASS的闭环控制性能均较PSS有较大程度地提高。RASS的频域性能较FASS有一定的损失,但在人体对振动的敏感频段垂直方向4～8Hz、旋转方向1～2Hz上,幅频增益均有较大程度地减小,提高了车辆的乘坐舒适性能;从左前轮位移输入至悬架动扰度、悬架作动器控制力的幅频响应亦为接近。

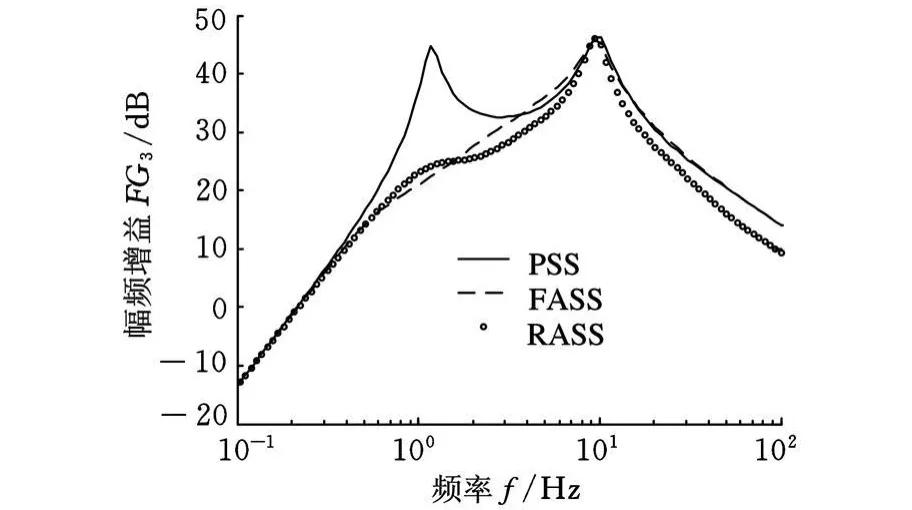
图6 x gA至φ¨的传递函数的幅频增益

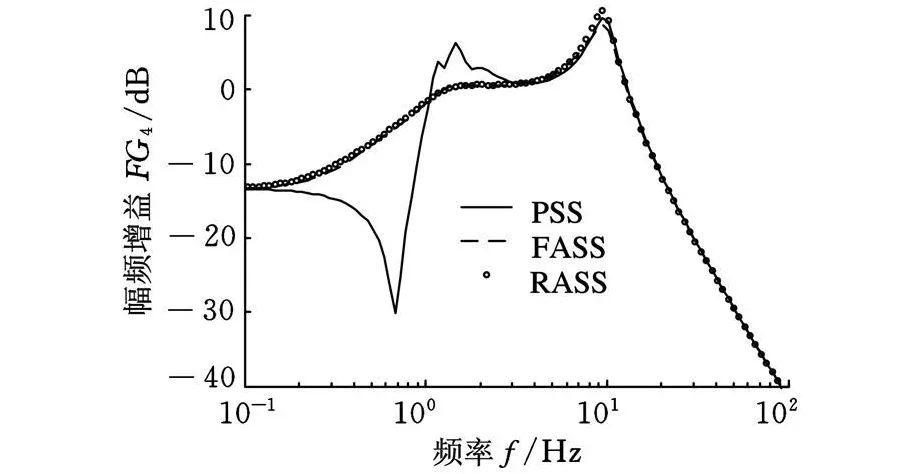
图7 x gA至(x bA-x wA)的传递函数的幅频增益

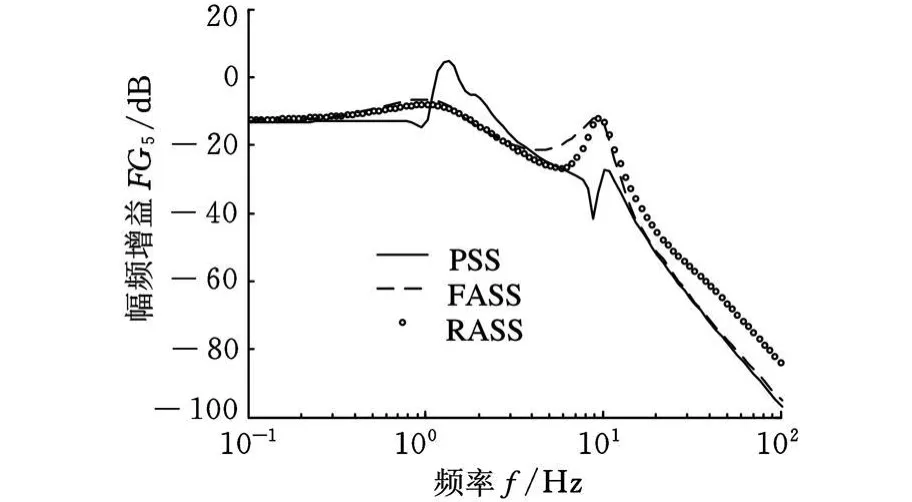
图8 x gA至(x bB-x wB)的传递函数的幅频增益

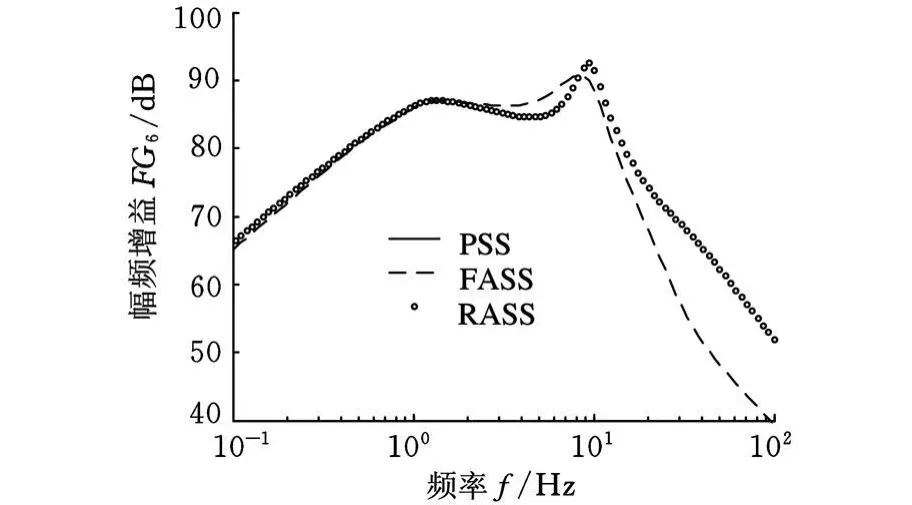
图9 x gA至fA的传递函数的幅频增益

5 结论

本文首先建立了整车7自由度主动悬架14阶动力学模型,考虑高频动态未建模不确定性和人体对振动的敏感频段,设计了频率加权广义主动悬架系统H∞控制器,以获得对路面干扰具有较好的抑制效果。

针对所设计的高达28阶悬架控制器,采用频率加权右互质分解的控制器降阶方法进行降阶,所得到的各阶降阶悬架控制器均能够保证闭环系统稳定。全阶、降阶悬架闭环控制系统乘坐舒适性能比较和频域仿真结果分析表明:基于频率加权右互质分解的控制器降阶方法能较大程度地降低控制器的阶数,且保证降阶闭环悬架控制系统的性能损失较小。这将为下一步高阶悬架控制器的简化工程的实现提供理论支持与技术保障。

[1] YamashitaM,Fujimori K,Hayakawa K,et al.App lication of H∞Control to Active Suspension Systems[J].Automatica,1994,30(11):1717-1729.

[2] Abdellahi E,Mehdi D,M'Saad M.On the Design of A ctive Suspension System by H∞and M ixed H2/H∞:an LM I Approach[C]//Proceedings of the American Control Con ference.Chicago,2000:4041-4045.

[3] 韩波,王庆丰.电液主动悬架的H∞控制研究[J].汽车工程,2000,22(2):77-80.

[4] Lohmann B.Application ofModelOrder Reduction to a Hydropneumatic Vehicle Suspension[J].IEEE Transactions on Control Systems Technology,1995,3(1):102-109.

[5] Kim C,Ro P I.An Accurate Full Car Ride Model U-sing Model Reducing Techniques[J].Journal of Mechanical Design,2002,124(12):697-705.

[6] Wang J,Xu W,Chen W.Op timal Hankel-norm Reduction of Active Suspension Modelwith Application in Suspension Mu ltiobjective Control[J].Int.J.Vehicle Design,2006,40(1/3):175-195.

[7] Amirifa R,Sadati N.A Lower-order H∞Controller Design for an Active Suspension System via Linear Matrix Inequalities[J].Journal of Vibration and Control,2004,10:1181-1197.

[8] Dave C,喻凡.车辆动力学及其控制[M].北京:人民交通出版社,2003.

[9] Ikenaga S,Lewis F L,Campos J,et al.A ctive Suspension Control of Ground Vehicle Based on a Fu ll-vehicle Model[C]//Proceedings of the American Control Conference.Chicago,2000:4019-4024.

[10] Varga A.On Frequency-weighted Coprime Factorization Based Controller Reduction[C]//Proceedings of the American Control Con ference.Denver,2003:3892-3897.

[11] Wang J.Generalized Multi-ob jective Control with Applications to Vehicle Suspension Systems[D].Leeds UK:University of Leeds,2003.

Controller Order-reduction for Fu ll-vehicle Active Suspension System Based on Frequency-weighting Method

Huang Changxi Wang Hongbo
Hefei University of Technology,H efei,230009

A dynamicsmodel for a full-vehicle active suspension system w ith 7 degree-of-freedom wasbuilt.Considering the factorsof high-frequency dynam ic uncertainties and human's sensitive frequency ranges to vibration,aweighted H∞controller for the generalized suspension system was designed to restrain the road disturbances.Frequency-weighted coprime factorization based controller reduction method wasutilized to reduce the order of the obtained high-order controller.Through ride com fort performance comparision and frequency-domain sim ulation analyses,the research results dem onstrate that the order of high-order controller can be reduced significantly,and the reduced-order suspension closed-loop control system can obtain the similar control performance with the full-order one.

active suspension;H∞control;frequency weighting;controller order-reduction

U461

1004—132X(2011)11—1366—04

2010—08—02

(编辑 苏卫国)

黄长喜,男,1974年生。合肥工业大学电气与自动化工程学院副研究员。研究方向为风电系统控制、现代控制理论及其应用。汪洪波(通讯作者),男,1981年生。合肥工业大学机械与汽车工程学院讲师、博士研究生。