一种基于线性物理规划和两级集成系统综合方法的多目标多学科优化方法

陶友瑞 韩 旭 姜 潮 刘迎春

1.湖南工程学院,湘潭,411104 2.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

一种基于线性物理规划和两级集成系统综合方法的多目标多学科优化方法

陶友瑞1韩 旭2姜 潮2刘迎春1

1.湖南工程学院,湘潭,411104 2.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082

提出一种高效、直观的方法来解决多目标多学科设计优化问题。在该方法中,设计者首先确定线性物理规划中各目标的偏好类型及偏好值,然后利用ε约束法将多目标问题转换成单目标问题,再采用两级系统集成综合方法进行多学科设计优化,得到不同设计优化方案,最后采用线性物理规划评价各设计方案的优劣并得到最优方案。采用该方法对一个工程实例(减速器模型)进行了优化,从5个设计方案中求得了最优设计方案,最优解中的两个目标函数值都在可容忍区间,从而也验证了该方法的有效性。通过该算例也说明该方法具有很好的工程应用价值。

多学科设计优化;多目标优化;线性物理规划;两级集成系统综合方法

0 引言

多学科设计优化(MDO)是一种用于大型系统的并行设计方法,是一种通过充分探索和利用系统中相互作用的协同机制来设计复杂系统工程和子系统的方法论,目前已经成为优化设计领域的研究热点,主要应用于航空航天领域[1]。在工程问题中很多学科设计优化问题是多目标问题,由于多目标优化问题一般不存在单个最优解,因此希望求出其Pareto最优解集,然后根据Pareto前沿的分布情况进行多目标决策。求解Pareto最优解集传统的方法是将多目标问题转换为多个不同的单目标优化问题,用单目标优化方法分别进行求解,这些单目标最优解对应原多目标优化问题的Pareto最优解,用这些解的集合去近似Pareto最优解集。求解方法主要有加权法和约束法[2]。

在多学科设计优化研究的早期,包括协同优化(CO)策略在内的所有的MDO策略只能处理单目标的多学科优化问题。近年来,研究人员开始关注多目标多学科设计优化问题。Tappeta等[3]对协同优化策略进行了改进,使其能够处理多目标问题,在该方法中,采用加权法将多目标问题转换为单目标问题。Sobieszczanski-Sobieski等[4]的研究表明,加权法用于设计空间的搜索是有效的。Zhang等[5]将自适应的权系数方法引入并行子空间优化(concurrent subspace optim ization,CSSO)策略中,得到了一种新的处理多目标多学科问题的方法,该方法可以用来处理大规模变量的问题。但是,加权法的主要缺点是对Pareto前沿非凸的情形不能求出所有Pareto最优解,而且多个目标之间往往不可比较,从而限制了其应用。Huang等[6]也对CSSO处理多目标问题进行了研究,采用约束方法使CSSO在多学科设计优化的框架中处理多目标问题。然而,该方法只用于求得Pareto最优解,而不能直接得到满足设计者偏好的Pareto最优解,另外,约束法的主要缺点是约束边界值变化范围的确定需要先验知识。

物理规划由美国学者Messac[7]于1995年提出,它是一种新的处理多目标优化问题的有效方法。物理规划能从本质上把握设计者的偏好,无需反复设置各个目标的权重系数,大大减轻了大规模多目标设计问题的计算负担,并将整个设计过程置于一个更加灵活、自然的框架中。它通过综合偏好函数将工程设计问题中的多目标优化问题转换为单目标优化问题,获得反映设计者偏好的最优设计。线性物理规划(LPP)是物理规划的特殊形式,用于处理线性问题。M cA llister等[8]将线性物理规划方法引入协同优化策略中,用于处理多目标多学科问题。在该方法中,设计者可以采用有物理意义的参数来描述多个系统级的目标。毫无疑问,该方法扩展了协同优化的应用范围,也为线性物理规划方法在多学科设计优化中的应用打下了基础。但是协同优化策略本身存在优化结果可能不收敛的缺陷,故该方法的应用也受到相应的影响。因此,寻求线性物理规划方法在其他多学科设计优化策略中的应用势在必行。

两级集成系统综合(bi-level integrated system synthesis,BLISS)方法是Sobieszczanski-Sobiesk等[9]在1998年提出的一种基于分解技术的工程系统多学科设计优化方法,由于它具有可以处理多变量和较容易人为干预优化过程的独特优点而被认为是性能最强的一种多学科优化策略。BLISS方法只能处理单目标的多学科优化问题,本文欲将线性物理规划方法嵌入到BLISS中,使其能处理多目标多学科问题。

1 多目标多学科问题的描述

与单学科问题不同,在多学科问题中各学科之间存在耦合关系,因此多目标多学科问题较单学科多目标问题复杂。多目标多学科问题可描述如下:

式中,X为系统设计向量;X1,X2,…,Xn为各子系统的设计向量;y1,y2,…,yn为学科状态变量;y1i,y2i,…,yni为耦合状态变量;g为不等式约束;H为系统分析中必须满足的方程。

2 多目标多学科优化方法的建立

由于多学科优化问题本身非常复杂,因此在多目标多学科优化中要求得所有的Pareto最优解的计算成本将会很高。一般而言,从工程应用的角度出发,设计人员希望能够从少量的Pareto最优解中找到能够满足设计人员偏好的最优解。本文提出的多目标多学科设计优化新方法中,设计者的偏好采用具有物理意义的参数进行描述,采用约束法将多目标问题转换为单目标问题,利用BLISS求解Pareto最优解,最优方案通过线性物理规划进行评价。

2.1 线性物理规划

线性物理规划通过偏好函数来表达设计者的偏好程度,将设计目标的取值范围按不同的满意程度等级(满意,可以容忍,不满意等)划分为若干连续区间,以反映设计者的各种偏好程度[7]。在线性物理规划中,偏好函数有4种类型,根据偏好精确度的不同,每一类包括软、硬两种情况。软偏好函数对应优化设计问题的设计目标,硬偏好函数对应约束条件。4种类型的软偏好函数定义为:①目标最小化(1S);②目标最大化(2S);③目标趋于某定值最好(3S);④目标趋于某区间最好(4S)。

采用线性物理规划进行多目标优化的步骤如下:

(1)设计者根据问题的性质规定各设计目标的偏好函数类型(软型或硬型)。

(2)为各定量及非定量的设计目标规定用数值表示的满意程度区间。

(3)利用决策者在规定的各设计目标偏好函数类型及满意程度区间来计算线性物理规划数学模型中的递增权值

2.2 BLISS方法

BLISS方法的基本思想是将系统层优化从潜在的众多子系统优化中分离出来,使得系统层设计变量显著减少。BLISS运行之初要先对系统设计变量赋初始值,然后通过循环来改进设计变量以达到最优[9]。每次循环都由两步组成:第一步,冻结系统层变量,对子系统层内的局部设计变量进行独立的、并行的、自主的优化;第二步,在第一步的基础上优化系统层变量以达到更进一步的优化,在进行子系统优化之前要进行系统分析及灵敏度分析。

2.3 基于LPP和BLISS的多目标多学科优化流程

多学科设计优化中面临的困难是结构复杂和计算量巨大,而且多学科设计优化中还可能包含多个相互矛盾的优化目标,因此,多目标多学科设计优化是一个更为复杂的问题。本文将线性物理规划应用于多目标多学科设计优化之中,提出一种高效、直观的方法来解决该问题。首先,设计者确定线性物理规划中各目标的偏好类型及偏好值,即设定各目标5个满意程度区间的边界值,然后利用ε约束法将多目标问题转换成单目标问题,即将多个目标中的一个作为优化目标,其余的目标转换为约束,且该约束的上界设定为某一个满意程度区间的边界值,再采用两级集成系统综合方法进行多学科设计优化,从而得到一个设计优化方案(即一个非劣解)。当改变目标约束上界并且重新进行多学科设计优化时,就可得到多个设计方案(即多个非劣解)。各设计方案的优劣采用线性物理规划评价模型来实现,在该模型中先计算线性物理规划数学模型中的递增权值,再计算各设计方案的综合目标函数值,综合目标函数值最小的方案为最接近设计者意愿的方案,即最优方案。

该方法的优化流程如图1所示,具体过程如下:①初始化所有的设计变量及耦合变量,i=0,j=0,i为第i偏好区间,j为第j个由目标转换而来的附加约束;②设计者确定各目标所属的类型(硬型或软型),并为各目标的偏好区间确定端点处的设计目标值;③初始化εj,εj=t(j,1),εj为附加约束的上界,t(j,1)为第j个附加约束的第1个偏好区间端点处的设计目标值;④j←j+1;⑤i←i+1;⑥通过约束法将多目标问题转换为单目标问题,t(j,i)表示第j个附加约束的第i个偏好区间端点处的设计目标值;⑦采用BLISS方法优化转换后的单目标多学科问题,得到一个设计方案,即一个Pareto点;⑧如果第j个附加约束的所有的偏好区间已经全部被选作约束上界,则转 ⑨,否则转⑤;⑨如果j＞tota l,转 ⑩,否则转 ④,tota l为附加约束的总个数;⑩采用线性物理规划方法对求得的所有设计方案进行评价,得到最优设计方案。

与传统的多目标优化方法相比,如与多目标遗传算法相比,本文所提出的方法可以大大减小计算量,其原因在于减少了求解 Pareto点的个数,但同时又能够满足设计人员的偏好。例如,对于一个两目标的多学科设计优化问题,所求的Pareto点只有5个,对一个三目标的多学科设计优化问题,所求的Pareto点也只有25个。另外,多目标中经常存在目标量纲不同以及目标的量级不同的情况,该方法也易于处理这一类问题,其原因在于在线性物理规划方法中对各目标值进行了归一化处理。

图1 基于线性物理规划和BLISS的多目标多学科设计优化流程

3 应用

3.1 算例介绍

模型为一个减速器优化模型[10],其原始模型的目标函数为使减速器的体积最小,约束为应力、挠度及尺寸约束。设计变量为齿轮尺寸(x1,x2,x3)和传动轴尺寸(x4,x6,x5,x7),模型如图2所示。

图2 减速器模型

本文将该模型改造为两目标问题,即体积 f1最小和齿轮应力 f2最小,模型的数学表达如下:

3.2 优化求解过程

该模型虽然不太复杂,但它是一个典型的多目标多学科问题,能够作为一个很好的算例来对本文所提的方法进行验证。首先,确定各目标的类型,在本模型中目标 f1和目标 f2均为1S型。然后为各目标确定各偏好区间端点处的设计目标值,如表1所示。

表1 目标函数的类型及偏好区间的设计目标值

在两个目标中需要将其中一个转换为附加约束,本文取f1为优化目标,将f2转换为附加约束。所以,目标 f2的各偏好区间端点处的设计目标值将作为附加约束的上界。在进行多学科设计优化之前,需要对该模型进行处理以便能够采用BLISS方法进行优化。将该模型分解为3个子系统:D1、D2、D3。各系统的定义如下式所示(x1、x2、x3为系统设计变量,x4、x5为子系统D1的设计变量,x6、x7为子系统D2的设计变量):

3.3 结果和讨论

采用本文提出的优化方法对上述多目标多学科优化问题进行求解,得到5个设计方案,如表2和图3所示。从结果中可以看出没有一个设计方案是完全理想的,因此只有从5个设计方案中选出一个最能够满足设计者偏好的方案为最优设计方案。通过线性物理规划方法对各方案进行评价,方案3的综合目标函数值最低,最接近设计者的偏好,在该方案中,体积1925和应力4,都在可容忍区间内。各设计变量的取值为[2.6,0.435 86,17,7.3001,7.7167,3.3609,5.2879]。

表2 优化结果

得到该最优方案后,设计者根据实际情况决定是否接受该方案。如果认为该方案还没有满足要求,设计者可以在第一次优化的基础上寻求更优的设计方案,即重新对该问题进行优化。具体方法如下:选出综合目标函数值最低和次低的两个方案,在这两个方案之间重新定义设计者的偏好区间端点处的设计目标值,如表3所示。

图3 第一次优化后Pareto点的分布

表3 目标函数的类型及偏好区间的设计目标值

确定了偏好区间端点处的设计目标值后,采用本文提出的方法重新对该问题进行优化,得到的设计方案如表4和图4所示。从各方案的综合目标函数值可以看出方案4为最优方案,其体积为1966,应力为3.5。与上一次优化结果比较可以得知该方案更加接近设计者的偏好。毫无疑问,优化还可以重复进行,但其前提是设计者可以接受其计算成本的增加以及设计者是否可以接受已经得到的方案。

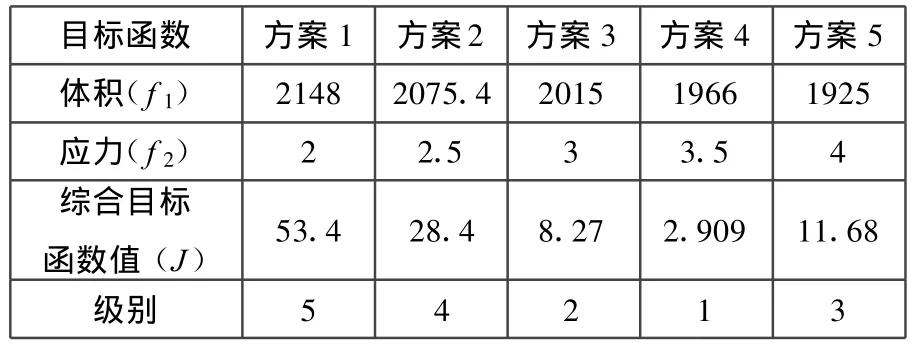
表4 优化结果

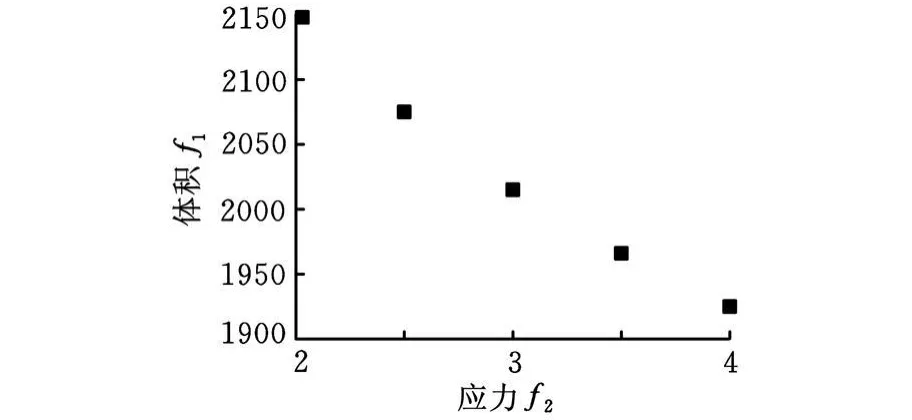
图4 第二次优化后Pareto点的分布

4 结语

BLISS方法是一种性能好的多学科设计优化方法,但传统的BLISS方法仅仅能够处理单目标问题。本文将线性物理规划方法嵌入到BLISS方法中,提出了一种新的处理多目标多学科问题的方法,并采用工程实例对该方法的性能进行了评价。由于该方法只需要求得少量的Pareto点便能得到满足设计偏好的最优设计方案,因此该方法具有计算成本低的优点。同时,多目标问题中经常存在目标量纲不同以及目标的量级不同的情况,该方法也易于处理这一类问题。所以,本文所提出的方法适于处理工程问题中的多目标多学科设计优化问题,具有很好的工程应用价值。

[1] 王振国,陈小前,罗文彩,等.飞行器多学科设计优化理论与应用研究[M].北京:国防工业出版社,2006.

[2] 陈琪锋,戴金海.多目标的分布式协同进化MDO算法[J].国防科技大学学报,2002,24(4):11-15.

[3] Tappeta R V,Renaud J.Mu lti-ob jective Collaborative Op tim ization[J].Journal of Mechanical Design,1997,119(3):403-411.

[4] Sobieszczanski-Sobieski J,Venter G.Imparting Desired A ttributes in Structural Design by Means of Mu lti-objective Optim ization[J].Struct.Multidisc.Op tim.,2005,29(6):432-444.

[5] Zhang Keshi,Han Zhonghua,LiW eiji,et al.Bileve l Adaptive W eigh ted Sum Method for Multi-Objective Optim ization[J].A IAA Journal,2008,46(10):2611-2624.

[6] Huang C H,Galusk J,Bloebaum C L.Multi-objective Pareto Concurrent Subspace Optim ization for Mu ltidisciplinary Design[J].A IAA Journal,2007,45(8):1894-1907.

[7] Messac A.Physical Programm ing:Effective Optim ization for Computational Design[J].A IAA Journal,1996,34(1):149-158.

[8] M cA llister C D,Simpson T W,H acker K,et al.Integrating Linear Physical Programm ing Within Collaborative Optim ization for Multiobjective Multidisciplinary Design Optimization[J].Struct.Multidisc.Op tim.,2005,29(3):178-189.

[9] Sobieszczanski-Sobieski J,Agte JS,Jr Sandusky R R.Bi-level Integrated System Synthesis(BLISS),A IAA-98-4916[R].H ampton,V irginia:Langley Research Center,1998.

[10] 陈伟,杨树兴,赵良玉.BLISS方法的基本理论及应用[J].弹箭与制导学报,2007,27(5):229-234.

AMulti-objectiveMultidisciplinary Design Optimization Method Based on
Integrating Linear Physical Programming and Bi-level Integrated System Synthesis

Tao Yourui1Han Xu2Jiang Chao2Liu Yingchun1
1.Hunan Institute of Engineering,Xiangtan,Hunan,411101 2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body,Hunan University,Changsha,410082

We present a novelmethod to deal w ith multi-objectivem ultidiscip linary design optimization by integrating linear physical programming with bi-level integrated system synthesis.A t first,designers decided to which criterion class theobjectives belong,and choose the range targets for every ob jective.Then themu lti-ob jective p rob lem w as converted to sing le-ob jective p rob lem with-constraintmethod.Bi-levelintegrated system synthesiswas used to solve themu ltidiscip linary design op timization p roblem.A ll design schemeswere evaluated by linear physical p rogramming and the op timum design scheme can be obtained.A speed reducerm odel w as investigated to demonstrate the performance o f the presented method.The op tim al design scheme can be obtained from five design schemes.The volume and stress of the op timal design schem e are in the tolerab le range.The presented method can be app lied in the engineering problems.

m ultidiscip linary design optimization;multi-objective optimization;linear physical programming;bi-level integrated system synthesis

TH 122

1004—132X(2011)11—1357—05

2010—03—02

国家科技重大专项(2010ZX04017-013-005);国家自然科学基金资助项目(51075138);湖南工程学院 2011年科研启动基金资助项目

(编辑 苏卫国)

陶友瑞,男,1973年生。湖南工程学院机械工程系副教授、博士。研究方向为多学科优化设计、材料成形工艺与仿真。发表论文 15篇。韩 旭,男,1968年生。湖南大学机械与运载工程学院院长、教授、博士研究生导师。姜 潮,男,1978年生。湖南大学机械与运载工程学院副教授、博士。刘迎春,男,1951年生。湖南工程学院副校长、教授。