基于有限元法的移动2杆柔体机械手动力学仿真

杨玉维 赵新华 王收军 徐进友 陈 炜

天津理工大学天津市复杂系统控制理论及应用重点实验室,天津,300384

基于有限元法的移动2杆柔体机械手动力学仿真

杨玉维 赵新华 王收军 徐进友 陈 炜

天津理工大学天津市复杂系统控制理论及应用重点实验室,天津,300384

研究了移动2杆柔体机械手动力学问题。该移动机械手由弹性-阻尼悬架轮式移动载体和2杆柔体机械手组成,并假定移动载体以恒线速度通过不规则路面。综合采用经典有限元法并引入中间单元坐标系和浮动坐标法,以回避由单元刚体运动所导致的弹性构件非零应变,从而精确描述机械手弹性变形与参考运动间的动力学耦合问题。综合利用拉格朗日原理和牛顿-欧拉方程并在笛卡儿坐标系下 ,以简洁的矩阵、矢量形式构建了该系统的完整动力学模型。采用数值方法给出了该动力学模型正解的仿真结果。通过与刚-柔体模型、刚体模型仿真结果的比较,证实该柔体系统存在动力学耦合现象及构件弹性振动对系统性能有负面影响。

2杆柔体;移动机械手;有限元法;运动学;动力学;耦合

0 引言

近年来,高速、轻质和高精度的移动机械手的研究倍受关注。由于用于描述由柔性机械手与具有悬架系统的轮式移动载体所组成的移动机械手的系统动力学方程具有非线性、高耦合性及非完整约束的特点,致使推导和求解柔性机械手的运动学方程、动力学方程相当繁杂。当前,研究者对移动机械手动力学模型的建立与控制显示出了极大的兴趣,然而通常情况下,他们的动力学模型中没有考虑悬架的影响,移动载体的自由度被悉数加到机械手上,该移动机械手被视为冗余度机械手。Akpan等[1]研究了平面移动机械手性能对系统参数如刚度、阻尼、路面粗糙度等的敏感度问题;Yu等[2]介绍了一个用于推导移动机械手动力学的通用方法,定义了移动平台与机械手之间的耦合术语,然而这个移动平台只能做平面运动,且他们也没有考虑构件的弹性变形问题;Korayem等[3]采用Lagrange法和关节坐标构造了移动机械手的动力学模型,该模型考虑了机械手的平面弹性小变形和轮子的非完整约束,但该方法建立在线弹性动力学基础上,没有考虑构件弹性变形与构件大范围运动间动力学耦合问题;文献[4-6]考虑了机械手的柔性,构建了动力学模型,并推导了该移动机械手的最大承受载荷。以上研究工作中的动力学模型皆没有包括悬架系统。

文献[7-8]研究了轮式悬架移动机械手动力学问题,但该动力学模型没有考虑机械手的弹性变形问题。

经典有限元法中,由于梁单元为非等参单元,这类单元离散后杆件模型做任意刚体运动时,单元内将导致非零应变,从而使构建的动力学模型不能准确描述系统运动特性。基于梁单元型函数可以准确描述刚体平动这一特性[9],本文引入构件体坐标系(浮动坐标系)为中间单元坐标系,精确构建了移动2杆柔体机械手动力学模型(可以精确描述构件刚体运动)。该模型综合考虑了机械手杆件的弹性变形、移动载体的线弹性-阻尼悬架和不平路面等工况。

1 运动学、动力学模型分析、推导

图1 移动2杆柔体机械手

移动2杆柔体机械手由3个构件组成,如图1所示,其中,Kk、Ck(k=1,2)分别为该移动机械手悬架系统的弹簧刚度和阻尼系数;构件1、2、3分别为移动载体、机械手弹性杆件1和弹性杆件2。图 2为图 1平面化后的分析简图,其中,G(i)(i=1,2,3)为构件i的重力;F P为外荷载;F1为移动载体水平驱动力;F2、F3为(悬架)作用于移动载体上的力;Ox(0)y(0)、O(i)x(i)y(i)分别为轮式悬架柔性移动机械手的全局坐标系与构件i(i=1,2,3)的体坐标系[9]。本文假设:该车轮为刚体且无质量;该移动载体以恒线速度运行在不规则(可用正弦函数来描述)路面上。如图2、图3所示,构件3上任一点相对Ox(0)y(0)原点的位置矢量为

图2 移动2杆柔体机械手工况

图3 构件i(i=2,3)有限元离散

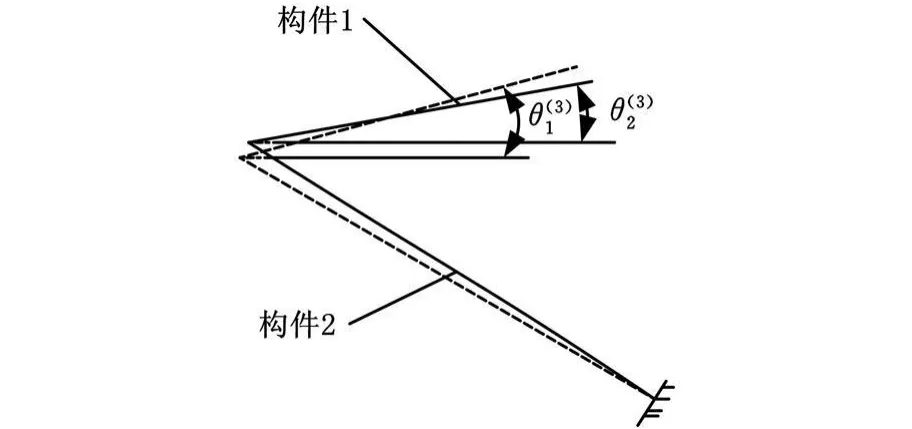
图4 机械手柔性构件弹性变形

该动力学模型的推导包括系统惯性张量、刚度矩阵、广义力、型函数等的推导过程。

1.1 构件2、3型函数推导

本文采用有限元法,基于欧拉-伯努利梁单元理论(不考虑机械手的剪切变形)构造单元型函数[9]:

同理可得到S(2j)。限于篇幅本文仅将构件2、3分别离散为3个单元,如图3所示。

1.2 构件2、3刚度矩阵获取

应用应变能定义构件3刚度矩阵,则构件3单元j的变形能可表述为

1.3 惯性张量推导

首先对构件3惯性张量进行分析推导。构件3上任一点速度向量表示为

式中,M(3)为构件3的惯性张量;ρ(3)、V(3)分别为构件3的密度和体积。

同理可得到构件1、2的惯性张量。则该移动机械手系统惯性张量为

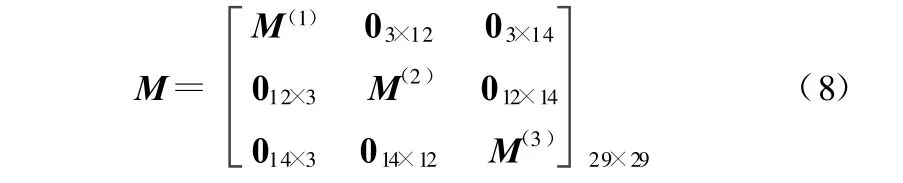
1.4 运动学分析

轮式移动机械手约束包括完整约束与非完整约束。完整约束来自机械手构件间转动副,参见图2。本文研究的移动机械手的轮子假设始终与路面接触(这也是后续判断该移动机械手失稳与否的判据之一),则移动机械手约束方程为

1.5 广义力推导分析

如图2所示,路面用正弦函数来描述,同时作用到移动载体上的F2、F3[10]可描述为

1.6 动力学分析、推导

依据拉格朗日方程,可以得到该移动机械手系统动力学方程:

式中,λ为拉格朗日乘子。

式(16)同时包含了常微分方程和代数方程,必须同时对其进行求解,这将增大求解难度,同时也加大了数值法求解时的累计误差等。为此,本文应用独立变量来表示系统动力学方程。将式(11)代入式(16)中,通过简化可以得到

2 动力学数值仿真

采用状态空间法描述上述动力学模型[9](式(17)),可得到

式(18)为一组常微分方程,则对系统动力学方程的求解问题转换为带初值的常微分方程求解问题。由于本文所考虑构件的弹性变形为小变形问题,所以柔性轮式移动机械手独立变量间存在数量级上的较大差异。因此,式(18)为刚性常微分方程组。基于Gear's法(高阶线性多步法),并采用MATLAB2006对式(18)进行数值法求解。数值仿真所用参数如下:m(1)=20kg,m(2)=0.9kg,m(3)=1kg;K 1=1130N/m,K2=2620N/m;C1=113N◦s/m,C2=262N◦s/m;d1=0.35m;t=0.35s;E=210MPa;l(1)=0.7m,l(2)=1.1m,l(3)=0.8m;d2=0.35m;g=9.8m/s2;l10=0.26m,l20=0.18m;构件2、3的半径分别为r2=0.007m,r3=0.007m;T(21)=-17N◦m,T(32)=40N◦m;λ=0.4m;v=0.3m/s;H0=0.03m,h=0.539m,c0=0;m p=5kg。部分数值仿真结果如图5～图8所示。

在相同参数下比较柔体动力学模型与其退化为刚-柔、刚体动力学模型的数值解,从图5、图6可以看出构件弹性变形、弹性振动对系统动力学性能的负面影响。如图5所示,由于考虑构件2、3的弹性变形及弹性振动,致使移动载体水平驱动力变化幅度、频率急剧增大;由图6所示的θ(2)的3种模型数值仿真结果可看出,随着时间的推移仿真结果出现较大的出入。这些充分体现出构件弹性变形与构件大范围参考运动间的动力学耦合效应及构件弹性振动对系统性能的负面影响。图7显示了该轮式移动柔性机械手独立系统变量θ(2)及其速度和加速度的变化趋势与规律:θ(2)变化平缓,其速度和加速度在零值上下快速波动,可以看出它们的变化规律符合变量对时间求导的规则。由图8可看出,构件2、3轴向刚度足够大,可以不考虑该方向的弹性变形问题。

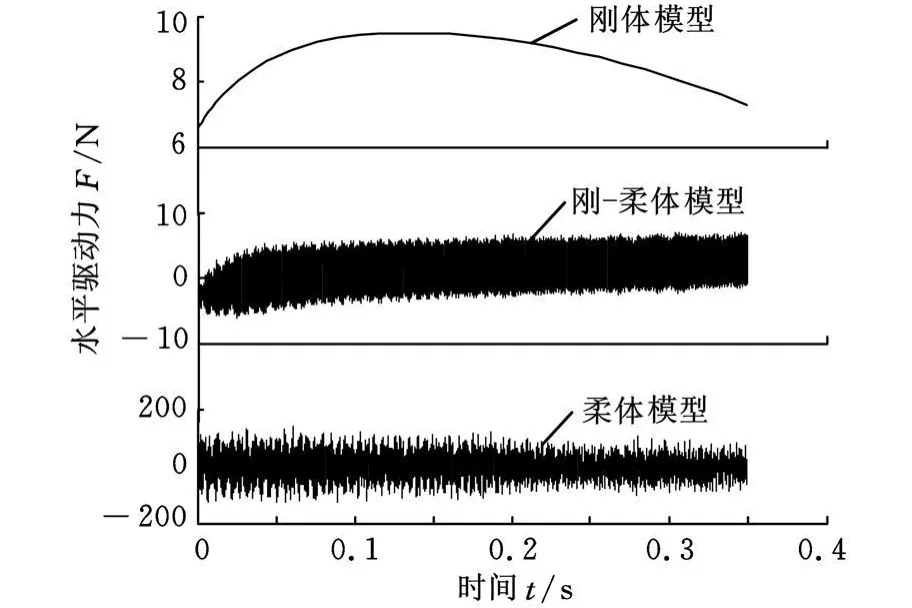
图5 移动载体水平驱动力

图 6 θ(2)数据仿真

图7 θ(2)、、数据仿真(柔体模型)

图8 构件2节点3弹性位移数据仿真

3 结论

本文对轮式弹性-阻尼悬架移动2杆柔体机械手运动学、动力学正解进行了系统研究。综合采用了有限元法和浮动坐标法,在笛卡儿坐标系下精确建立了系统动力学模型,并以矩阵、矢量的形式形成简洁的表达形式。由于中间单元坐标系的引入,使得该动力学模型可以精确描述构件刚体运动。相对关节变量而言,该方法更具有通用性,适用于大规模多体系统动力学分析,同时该动力学模型便于应用计算机进行数值求解。该动力学模型综合考虑了机械手的弹性变形(率)、弹性振动和悬架系统对整体动力学的影响。最后采用数值法给出了该动力学模型的正解仿真结果。通过该仿真结果可以看到上述动力学耦合现象及构件弹性振动的负面影响。该动力学模型和数值仿真可用作柔性轮式移动机械手参数设计之参考,并可指导选择相应控制策略等。

[1] Akpan U O,Kujath M R.Sensitivity ofaMobileManipulator Response to System Parameters[J].ASME Journal of Vibration and Acoustics,1998,120:156-163.

[2] Yu Q,Chen I.A General Approach to the Dynam icsof Nonholonom ic Mobile Manipu lator Systems[J].ASME Journa l of Dynam ic Ssystem s Measurements,and Control,2002,124:512-521.

[3] Korayem M H,Gharib lu H.Analysis o f W heel Mobile Flexibility Manipulator Dynam ic Motions w ith Maximum Load Carrying Capacities[J].Robotics and Autonomous System,2004,48:63-76.

[4] Korayem M H,Ghariblub H,Basu A.Optimal Load of Elastic Joint Mobile Manipu lators Imposing an Overturning Stability Constraint[J].Int.J.Adv.Manuf.Technol.,2005,26:638-644.

[5] Gharib lu H,Korayem M H.Trajectory Op tim ization o f Flexible Mobile Manipu lators[J].Robotica,2006,24:333-335.

[6] Korayem M H,Heidari A,Nikoobin A.Maximum A llow ab le Dynam ic Load o f Flexible Mobile Manipulators Using Finite Element Approach[J].Int.J.Manu f.Technol.,2008,36:1010-1021.

[7] Meghdari A,Durali M,Naderi D.Dynam ic Interaction between the Manipulator Andvehicle of a Mobile Manipu lator[J].Journal of Intelligent and Robotic Systems,2000,28:61-67.

[8] NaderiD,Meghdari A,DuraliM.Dynam ic Modeling and Analysis o f a Tw o DOFMobile Manipulator[J].Robotica,2001,19:177-185.

[9] Shabana A A.Dynam ics of Multi-body System s[M].Third Edition.Cambridge:Cambridge University Press,2005.

[10] 杨玉维,张明路,赵新华.七自由度柔性轮式移动机械手动力学研究与仿真[J].中国机械工程,2009,20(6):662-668.

Simulation of Dynam ics of a Mobile2-link Flexible Manipulator Based on Finite Element Method

Yang Yuwei Zhao Xinhua Wang Shoujun Xu Jinyou Chen Wei
Tianjin Key Laboratory for Control Theory&Applications in Comp licated System s,Tian jin University of Technology,Tian jin,300384

This paper concentrated on the kinematics and dynam icsm odeling of am obile 2-link flexib lemanipu lator(M 2LFM),which consisted of am obile basewith a 2-DOF linear elastic-damping suspension system and a flexib le manipu lator and was considered to travel w ith a constant linear speed over an irregu lar g round-surface.Based on Lagrange and New ton-Ou ler theories,the system dynamicsmodelof the M 2LFM in which the referencemotion and the elastic deformationwere coup led was derived using the finite elementmethod and intermediated element coordinatesystem s and floating frame of reference formulation which can lead to zero strains,and was com pactly described w ith matricesand vectorsmeasured with respect to a gobal Cartesian frame of reference.A t last,the numerical simulations were carried out to the forward dynamicsm odelof a M 2LFMand a rigid-flexibleone and a rigid one,respectively.These sim ulation results illustrate these effectsof dynam ic coup lingsand elastic vibration on system by comparion.

2-link flexible;mobile manipulator;finite element method;kinem atics;dynam ics;coup ling

TH 12

1004—132X(2011)11—1352—06

2010—06—28

国家高技术研究发展计划(863计划)资助项目(2006A A04Z221,2007AA 04Z203);国家自然科学基金资助项目(50675156);天津市应用基础与前沿技术研究计划资助重点项目(07JCZDJC09100);天津市高等学校科技发展基金资助项目(20100401)

(编辑 苏卫国)

杨玉维,男,1975年生。天津理工大学机械工程学院讲师。研究方向为移动机械手动力学。赵新华,男,1962年生。天津理工大学机械工程学院教授、博士研究生导师。王收军,男,1965年生。天津理工大学机械工程学院教授。徐进友,男,1977年生。天津理工大学机械工程学院讲师。陈 炜,女,1973年生。天津理工大学机械工程学院讲师。