组合法在电磁学中的巧用
2011-01-25赵强刘俊娟
赵强 刘俊娟
(石家庄机械化步兵学院 河北 石家庄 050083)
电磁学中的计算在根本上带有组合特点.由于电磁场的可叠加性,因此在计算各种电场、磁场时,可先将场源的基本关系进行组合,以求得最简便的处理过程.
将各种场源看作是点电荷、电流元的集合,当然是最基本的思路.但如果能够熟悉一些简单的典型场源所产生的场,如电偶极子、“无限长”均匀带电系统或电流系统,将场源看作是这些典型情况的直接组合,则不必再从头算起.这好像搭积木,一要熟悉基本构件,二要善于灵活组装.特别是,在组合场源时可以虚实并用.
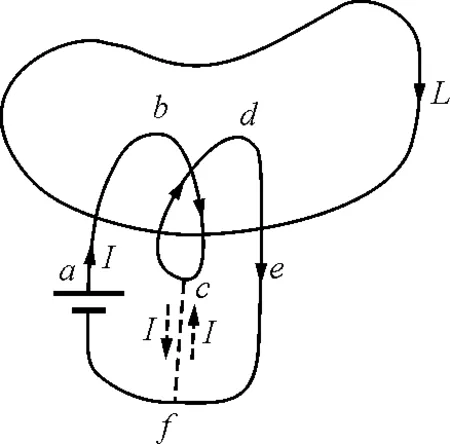
图1
例如,在安培环路定理的证明中,如果电流回路与积分回路是绞套的(图1),则可设想在c与f之间虚构一对强度为I的往返电流.这样,绞套的电流就转化为两个简单相套的电流,立即得出
∮LB·dl=2μ0I
这种虚实组合的方法,在电磁学里颇为有用,非常类似于平面几何证明题中添加辅助线的办法.只是这里是虚构,且在物理上应该是合理的,一般说来,不应该由虚构而破坏原有的物理状态.
现结合各种具体情况应用上述的组合方法,其中用无限远处作为“中转站”,做组合运算.
1 两金属球的互电容
【例1】两个半径都是a的金属球,球心相距d≫a(图2),求二者之间的互电容.
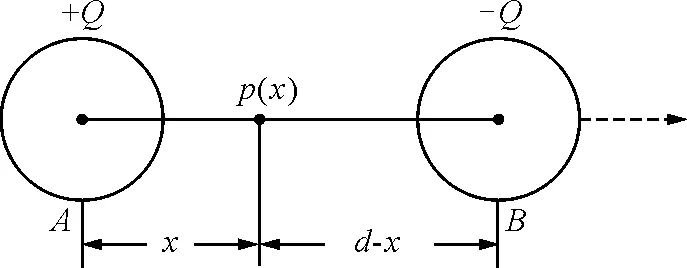
图2
解析:为了便于比较,采用两种计算方法.
(1) 常规计算
设两球分别带电±Q,由于d≫a,作为低级近似,可以认为这些电荷在各自的球面上均匀分布.于是,在球外中心联线上的任一点p(x),其场强方向都是沿x轴,场强大小为
而两球之间的电势差

由此即得所求的互电容为
(2)组合计算
以上计算假定各个球面上的电荷是均匀分布的,因此可以认为它们相距“无穷远”;所求电容是两个孤立小球电容串联,即
故
C=2πε0a
这里,将“无穷远”处作为一个中间的“联络站”.显然,组合计算比常规计算简洁得多.
2 内球接地的电容器
【例2】两同心金属球壳,壳厚可略;球壳半径R2>R1,若内球接地,求球壳之间的电容.
解析:所谓“接地”,是设法用极细、极长的导线与球外的地相连,而地是在“无穷远”处.当这个电容器充电时,两级之间的电势差U21即为外球壳与“无穷远”处之间的电势差U2∞.此时,不仅两极之间有电场分布,而且外球壳与“无穷远”之间也有电场分布.
于是,在这两个球壳之间并联着两个电容,即
所要求的电容,应该是它们的组合电容C.显然
3 动生电动势
【例3】一半圆形金属框,绕竖直轴以角速度ω均匀旋转,如图3(a)所示,稳恒磁场B是均匀的,且垂直图面向外.设半圆框的半径为R,求框的两个端点a,b之间的电势差.
解析:如果直接应用动生电动势的“切割磁感线”公式计算,则空间关系较繁琐,容易出错.为了能够运用法拉第电磁感应定律,可以在a,b之间虚构一条直导线,如图3(b)所示,从而构成闭合的半圆形回路.由于虚设的直导线ab在外磁场里是静止不动的,因此,闭合回路中的总感应电动势,仍然是原来半圆形金属框的动生电动势.

图3
按照图3(b)所选择的回路正方向,当外磁场B与半圆面夹角为φ时,B在半圆面上提供的磁通量为
于是,感应电动势

因为线段ab是虚设的,实际上半圆形金属框并不闭合,其中的感应电流为零(框内的自由电子迅速地达成平衡),故所求的电势差
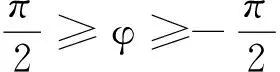
通过以上的例题分析可知,组合法在电磁学中的应用很广泛.掌握了这种方法使得解题过程既简便又快捷,而且可以提高分析问题和解决问题的能力.
参考文献
1 康颖. 大学物理(新版)第一版.北京:科学出版社,2005
2 杨庆芬,张闪,李同楷. 大学物理.北京:中国铁道出版社,2009
3 张三慧.大学物理学.北京:清华大学出版社,2004
4 马文尉.物理学教程.北京:高等教育出版社,2007
