基于自然单元法的动力学问题分析

房霆宸， 李 武

(1.上海大学 土木工程系， 上海 200072；2.中交第三航务工程勘察设计院有限公司， 上海 200032)

无网格法在动力学中的理论研究和应用已吸引了许多国内外学者，是计算力学中的一个研究热点[1]。自然单元法[2～6](Natural Element Method，NEM)是最近出现的一种无网格方法，自1995年Braun和Sambridge 在Nature上发表的《A numerical method for solving partial differ-ential equations on highly irregular evolving grids》一文提出自然单元法以来，以Voronoi图为几何基础的数值方法在国内外得到极大的关注.许多学者开展研究，并在不同的工程技术领域得到一定的应用。1998年，Sukumar N[3]将自然单元法成功地应用于求解固体力学中的椭圆型偏微分方程，并且构造了C1自然相邻节点插值成功求解了椭圆型四阶偏微分方程。在此阶段，NEM形函数的构造采用的是Sibson插值方法。2001年，Sukumar N[5]采用了Non-Sibsonian插值方法构造NEM形函数，从而使得NEM方法更为方便实用。Cueto E[6]基于α-shape的概念实现了三维分析。蔡永昌、朱合华等[7]研究了采用局部Petrov-Galerkin方法获得整体系统平衡的控制方程。卢波、葛修润等[8，9]研究了弱形式的数值积分方案，对自然单元法的原始应力数值解的精度进行了改善提高。在应用方面，Martniez M A[2，10]采用自然单元法求解了流体力学问题，朱合华、杨宝红[11]采用自然单元法求解了弹塑性问题。

无网格方法在动力学中得到广泛应用，自然单元法作为无网格方法的一种也应该被应用到动力学中。因此，本文详细推导和讨论自然单元法在动力学问题中离散方程和求解方法。

1 位移函数

1.1 近似位移函数

仿照二维Voronoi图的构建理论建立空间8结点的Voronoi图结构。本文采用立方体的顶点作为结点对空间进行划分，得到8结点的Voronoi结构，如图1所示。在图1中放入待插值点X，并对8个结点Voronoi图进行二次划分，得到待插值点X的二阶Voronoi结构的1/8部分，如图2所示。根据空球规则寻找自然相邻结点——若四面体的外接球包含待插值点，则该四面体的4个顶点即为待插值点的自然相邻结点。本文中采用的是立方体，再有本文四面体的外接球等价立方体的外接球，因此8个顶点既是待插值点X的自然相邻结点。

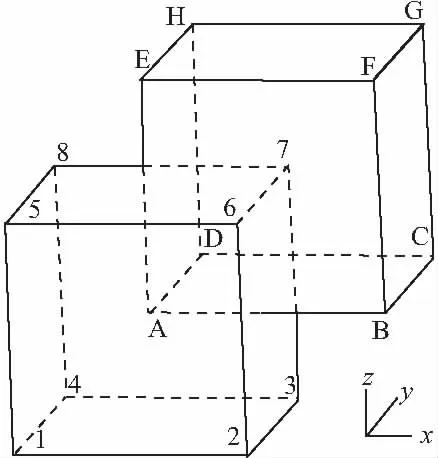
图1 8结点一阶Voronoi图

标号为1～8的8个结点构成了待插值点X的自然相邻结点，待插值点与自然相邻点一起形成Voronoi图称为待插值点的二次Voronoi结构。因为空间结构复杂，所以采用1/8结构进行说明推导过程。

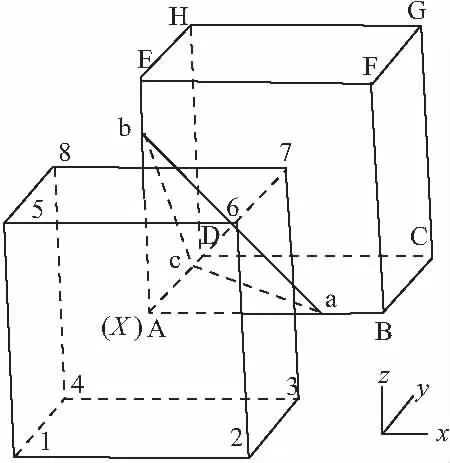
图2 8结点二阶Voronoi图

在图1、图2中1～8为空间结点，A～H为7结点的Voronoi图顶点；在图1中X为插值点，与A重合，X与8个结点形成二阶Voronoi图结构中的1/8部分，其中abc为X点二阶Voronoi图中3个顶点，取出与7结点相关部分的四面体Aabc，四面体Aabc为X的二阶Voronoi图与7结点一阶Voronoi图的重叠部分，而且直线A7垂直平面abc。根据图形对称性知道，其它7个结点的重叠部分与7结点相似，X的二阶Voronoi既是由8个四面体组成多面体。本文采用多面体相关边长建立函数。下面以7结点为例说明构建位移插值函数过程。

(1)

(2)

式中，S7(x)=ac+ab+bc是与结点7关联的Voronoi边的长度之和，h7(x)=A7是插值点x到结点7的Voronoi边组成平面的垂直距离(图2)。

把式(1)、式(2)中的7扩展为域内任意邻接点I的插值函数：

(3)

(4)

式中，SI(x)是与结点I关联的Voronoi边的长度之和，hI(x)是插值点x到结点I的Voronoi边组成平面的垂直距离。

1.2 三维位移插值函数的性质

由方程(3)的形函数构造过程可以很容易证明：

0≤ΦI(x)≤1

(5)

在图2中，可以注意到如果点x与任何结点重合，例如与结点7重合，则Φ7(x)=1，ΦI(x)=0(I≠7)。因此，该形函数与有限元法形函数一样，满足Kronecker条件：

ΦI(xJ)=δIJ

(6)

由式(3)可知，与有限元法一样，自然邻接形函数还满足单位分解条件和线性连续条件：

(7)

(8)

此外，自然邻接点的形函数除了在结点处C0连续外，在其它地方C∞连续。

1.3 三维位移插值函数的导数

根据插值函数式(3)、式(4)求导相应导数如下：

(9)

(10)

2 控制方程

平衡方程

σij,j(x,t)+fi(x,t)-ρ(x)ui,tt(x,t)-

μui,t(x,t)=0 (在Ω域内)

(11)

几何方程

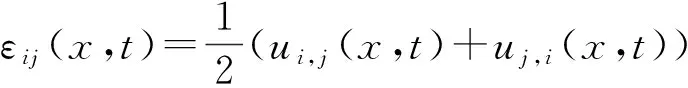
(12)

物理方程

σij(x,t)=Dijklεkl(x,t) (在Ω域内)

(13)

边界条件

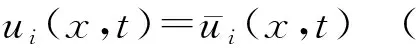
(14)

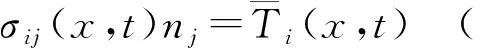
(15)

初始条件

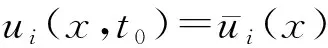
(16)

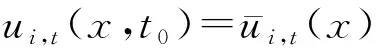
(17)

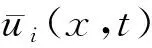
平衡方程(11)式及力的边界条件(15)式的等效积分形式的伽辽金表示法如下：

(18)

δui(x,t)ρui,tt(x,t)+δui(x,t)μui,t(x,t))dΩ

(19)

式中，δui(x,t)是任意变化的空间位移增量。

采用自然单元法对空间域进行离散，所以得到离散域内任意点x的位移u，v，w插值为：

(20)

(21)

(22)

式中，Φ(x)为结点插值的形函数，x为结点空间几何坐标。

将空间离散后的位移表达式(20)至式(22)(u(x,t)=u1(x,t),v(x,t)=u2(x,t)，w(x,t)=u3(x,t))代入(19)式得到系统求解方程如下：

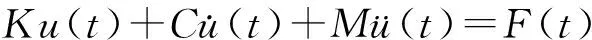
(23)

式中：

(24)

(25)

(26)

(27)

式中，M，C，K，F分别为质量矩阵、阻尼矩阵、刚度矩阵及荷载向量。

3 算例分析

通过以下算例，将本文方法与自然单元法(NEM)进行了对比。

为了对误差进行比较分析，定义位移误差范数Lu：

Lu=

(28)

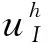
3.1 分片试验

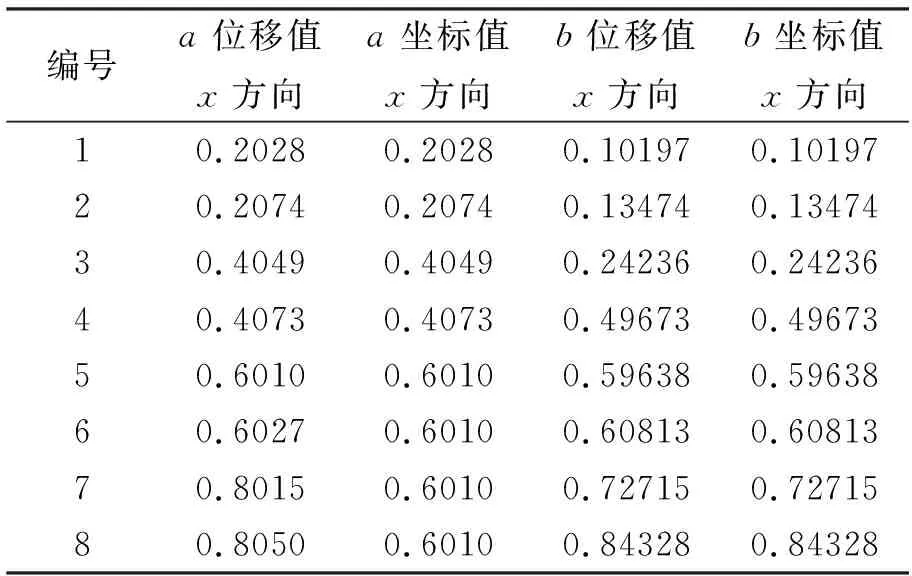
验算基于non-Sibsonian插值的三维自然单元法的收敛性，引入有限元中位移分片试验来验证本文程序的正确性。被检验Ω是立方体，如图3所示，采用均匀布点和非均匀布点两种离散方法，结点数为216、238，如图4、5所示。在立方体表面结点赋予该结点坐标作为给定位移，比较该立方体内部结点位移值ui与其坐标值。并在被检验Ω是立方体中任意选取8个节点，比较该立方体内部结点位移值ui与其坐标值，如表1。

图3 立方体

图4 均匀布点

图5 非均匀布点

编号a位移值x方向a坐标值x方向b位移值x方向b坐标值x方向10.20280.20280.101970.1019720.20740.20740.134740.1347430.40490.40490.242360.2423640.40730.40730.496730.4967350.60100.60100.596380.5963860.60270.60100.608130.6081370.80150.60100.727150.7271580.80500.60100.843280.84328

由表1可知本文三维自然单元法的算法可以精确通过分片试验，因此该算法解的收敛性通过分片试验的检验，说明本文算法是正确的、可行的。

3.2 悬臂梁端部受集中静载荷作用

三维弹性悬臂梁纯弯曲小变形状态的挠度解析解为：

(29)

(30)

(31)

式中，p为集中荷载，E为弹性模量，v为剪切模量，I为矩形截面惯性矩。

悬臂梁尺寸如下：l=4000，b=h=400，如图6。右端受集中力p=200，左端固定，不考虑梁自重，弹性模量E=210000 Pa，剪切模量v=0.25。采用解析法、自然单元法(采用结点间距为100的均匀和非均匀两种布点方案离散悬臂梁，如图7、8)、有限元法(采用单元尺寸为100的四面体单元和六面体单元来离散悬臂梁，如图9、10)等方法计算梁中心轴线上结点处的挠度曲线，如图11所示。

图6 三维悬臂梁几何图形

图7 三维悬臂梁均匀布点

图8 三维悬臂梁非均匀布点

图9 三维悬臂梁六面体单元划分

图10 三维悬臂梁四面体单元划分

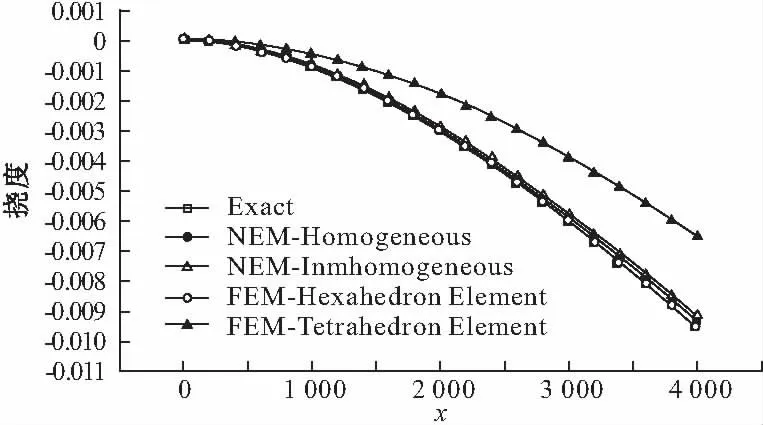
图11 悬臂梁沿y=0，z=0轴线上y方向位移比较

从图11可知，本算例在相同单元尺寸、结点间距的网格划分或布点下，四面体单元有限元法的结点最多，但是挠度值是解析解的70%左右，而均匀布点的自然单元法的计算精度比四面体精度明显提高，而且结点数也少于四面体单元。自然单元法的均匀布点和非均匀布点的计算结果都与解析解非常接近，精度与六面体单元在同一数量级上，如表2所示。对比自然单元法的两种布点方案，均匀布点比非均匀布点精度高，但是相差不大也在同一数量级上。再进一步研究自然单元法精度提高的原因发现，自然单元法的形函数中对于任意积分点搜索到自然邻接点在6个到20个之间，最普遍的是8个邻接点，并且这些邻接点多数都均匀分布在积分点周围，再根据连续物质的性质知，由这些邻接点插值出的形函数就比较接近连续物质真实形函数。这也就是为什么自然单元法的精度会与六面体在同一数量级原因。如果把四面体单元上进行结点加密，它也可以得到与自然单元法、六面体单元相同数量级的精度，见图12所示。

表2 自然单元法与六面体法数据对较表

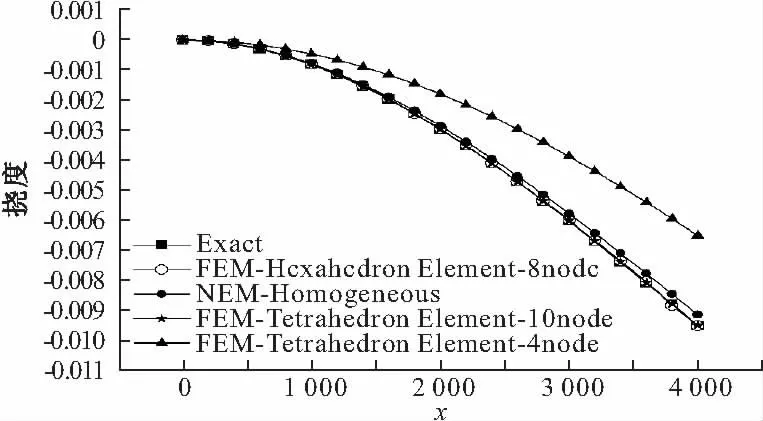
图12 不同插值点下的计算位移比较

3.3 悬臂梁端部受集中动载荷作用

悬臂梁尺寸如下：l=10 m，b=h=1 m，如图13。左端固定，不考虑梁自重，弹性模量E=210000 Pa，剪切模量v=0.25，密度ρ=2000 kg/m3，阻尼系数α=0.2、β=0.2。右端突然施加y向集中力p=g(t)，如图14，冲击作用时间t=4 s，时间步长Δt=0.01 s。为说明本文方法可行性，本文采用弹性小变形下，有限元软件Ansys的计算结果作为精确解，与本文方法相比较说明本文正确性。自然单元法(采用结点间距为0.5的均匀布点，如图15)、有限元法(采用单元尺寸为0.1六面体单元来离散悬臂梁，如图16)等方法分别计算无阻尼和有阻尼情况下，梁中心轴线上结点处的波形曲线，以及轴线中点和自由端点的时程曲线。

图13 三维悬臂梁几何图形

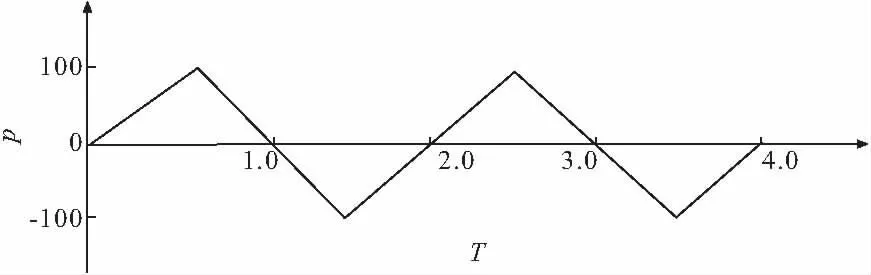
图14 输入荷载图波形

图15 三维悬臂梁均匀布点

图16 三维悬臂梁六面体单元划分

由图17可知，悬臂梁轴线在不同时间下，计算得到的无阻尼波形曲线与有限元法计算得到曲线非常接近。再由图18可知，两种方法计算的梁端点和中点的位移时程曲线也非常接近，因此说明本文方法在无阻尼情况下，能够像有限元法一样模拟弹性体的动力学问题。由图19可知，在有阻尼条件下，本文方法也可以模拟弹性体动力学问题。

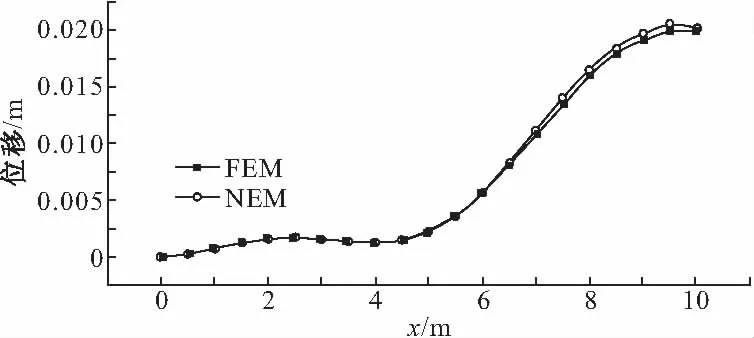
图17 无阻尼条件下轴线上y方向波形曲线

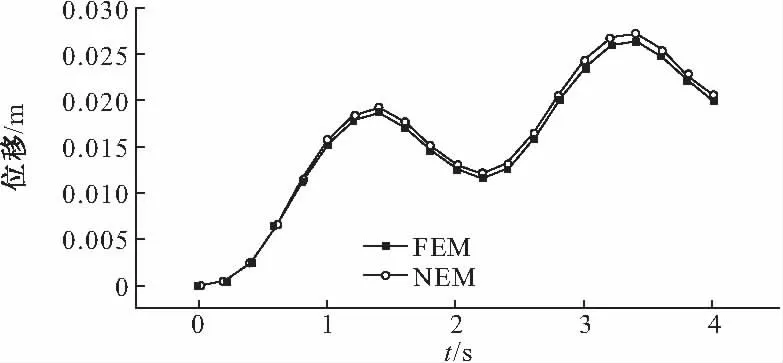
图18 无阻尼条件下点(10,0.5,0.5)y位移时程曲线

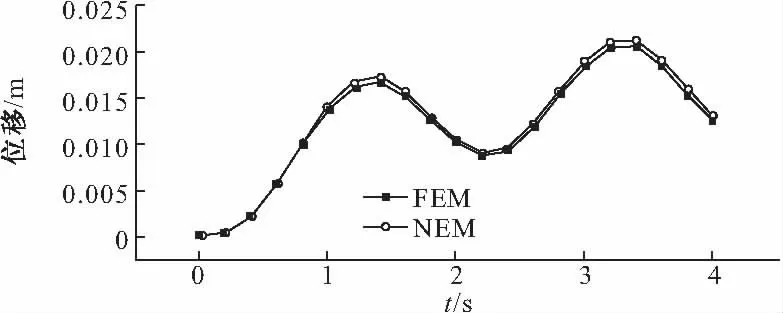
图19 有阻尼条件下点(10,0.5,0.5)y位移时程曲线

4 结 论

本文推导三维自然单元法的动力学问题的离散格式，空间域上采用本文推导的三维自然单元法的插值方法进行离散，时间域采用直接积分方法中的中心差分和Newmark常平均加速度法相结合的第一种积分格式进行离散。该积分方法可以消除加速度项，直接利用速度和位移联立方程组求解结点位移和速度。通过这种解耦方法提高了本文方法的计算效率。最后以分片试验、悬臂梁为算例，采用大型数值软件ANSYS模拟悬臂梁动力响应的计算结果作为基准，与本文推导的算法相对比，来验证本文算法的有效性和合理性。

对比本文方法和有限元方法，在弹性小变形条件下，两种方法都可以模拟计算弹性体动力学问，但是在大变形条件下，有限元方法将出现网格畸变使计算无法进行，然而本文方法则不会出现网格畸变，计算仍然可以进行。通过对比两种方法的计算结果可以知道，本文方法在很少结点情况下，可以得到与有限元数倍结点的计算结果相近。由此可看出，本方法受结点离散距离的影响较小，不像有限元在计算动力学问题时，受单元尺寸的限制，即单元尺寸要足够小，否则不能很好反映弹性体的动力特性。

[1] Dai K Y, Liu G R, Lim K M, et al. A mesh-free method for static and free vibration analysis of shear deformable laminated composite plates[J]. Journal of Sound and Vibration,2004,269(3-5):633-652.

[2] Braun J，Sambridge M. A numerical method for solving partial differential equations on highly irregular evolving grids[J].Nature，1995，376：655-660.

[3] Sukumar N. The natural element method in solid mechanics[D].Theoretical and Applied Mechanics，Northwestern University，1998.

[4] Sukumar N，Moran B，Belytschko T. The natural element method insolid mechanics[J]. International Journal for Numerical Methods in Engineering，1998，43(5)：839-887.

[5] Sukumar N，Moran B A. Semenov Y，et al. Natural neighbour Galerkin methods[J]. International Journal for Numerical Methods in Engineering，2001，50：1-27.

[6] Cueto E，Calvo B，Doblar′e M. Modeling three-dimensional piece-wise homogeneous domains using the α-shape based natural element method[J]. International Journal for Numerical Methods in Engineering，2002，54(6)：871-897.

[7] 蔡永昌，朱合华，王建华. 基于Voronoi结构的无网格局部Petrov-Galerkin方法[J].力学学报，2003，35(2)：187-193.

[8] 卢 波，葛修润，王水林.自然单元法数值积分方案研究[J] 岩石力学与工程学报， 2005，24(11)：1917-1924.

[9] 卢 波，葛修润，王水林.自适应自然单元法研究—误差估计[J].岩石力学与工程学报，2005，24(22)：4065-4072.

[10]Martniéz M A，Cueto E，Doblaré M，et al. A meshless simulation of injection processes involving short fibers molten composites[J].International Journal of Forming Processes，2001，4(3)：217-236.

[11]朱合华，杨宝红，蔡永昌，等.无网格自然单元法在弹塑性分析中的应用[J].岩土力学，2004，25(4)：671-674.