PC连续梁桥弯曲孔道摩阻损失

张开银， 黎 晨， 成 琛， 刘文波

(1. 武汉理工大学 交通学院， 湖北 武汉 430063； 2. 湖北省高速公路集团有限公司， 湖北 武汉 430000)

对于预应力混凝土连续梁桥、连续刚构桥，其结构具有刚度大、抗震能力强、行车平顺、易维护等优点。从国内外已建成的钢桥、钢筋混凝土及预应力混凝土连续梁桥的总数来看，预应力混凝土连续梁桥已远远超过半数，充分表现出该类桥梁结构强大的生命力。然而，许多运营中的桥梁结构，由于受多种因素的影响(如设计、施工、荷载、温度、材料等)，表现出不同类型的结构病害[1](如成桥混凝土箱梁跨中下挠、箱梁纵向开裂、腹板斜裂缝和结构局部损伤等)，严重危及着桥梁结构的营运安全和生命周期。

针对桥梁结构病害，国内外学者进行了大量的理论分析与试验研究，多数病害得到了较好的解决，但其中有些问题一直没得到统一的认识或结论。许多大跨度预应力混凝土桥梁结构的摩阻损失与理论计算值相差甚远，特别是混凝土构件受孔道偏差和孔道弯曲影响的不确定因素较多。有学者认为，在现行规范中，主要是对混凝土徐变的长期作用效应所引起的结构预应力损失估计不足[2]。理论与试验研究结果表明，在预应力束作用下，混凝土梁体将发生与结构应力状态一致的徐变。在目前三向预应力混凝土连续梁桥、连续刚构桥的设计中，混凝土箱梁是全截面受压，则徐变的作用效应只能表现为结构的压缩变形；而混凝土箱梁的跨中下挠，客观上表现为梁体的伸长，这一现象恰好与“混凝土徐变效应”是矛盾的。事实上，预应力连续梁桥、连续刚构桥徐变条件下的混凝土梁体伸长，表明箱梁处于拉应力状态，即结构的实际受力状态与设计受力状态正好相反。很多桥梁结构中存在的病害，均与现行规范对预应力结构摩阻损失估计不足有关[3]。

本文通过对预应力弯曲孔道摩阻损失计算理论的分析，指出了预应力弯曲孔道摩阻损失计算理论存在的严重缺陷；通过对弯曲孔道接触应力分布规律的探讨，比较了几种假设弯曲孔道接触应力分布下的预应力损失情况，为深入研究预应力弯曲孔道摩阻损失影响因素提供指导。

1 预应力弯曲孔道摩阻损失

现行预应力束摩阻损失[4]及延伸量计算表达式为

σs=σcon(1-e-(μθ+kl))

(1)

式中，σs为孔道摩阻损失(MPa)；σcon为预应力束锚端控制应力(MPa)；μ为预应力束与管道壁间的摩擦系数；θ为张拉端至计算截面长度上，管道曲线部分始端至终端弯起角绝对值之和(rad)；k为管道每米局部偏差对摩擦的影响系数；l为张拉端至计算截面管道长度(m)。

针对式(1)所表示的预应力摩阻损失计算式，可从如下几个方面探讨其不合理性。

首先，依据赫兹接触理论[5]，当两半径不同的光滑球体在法向荷载W作用下，其弹性接触情况如图1所示。

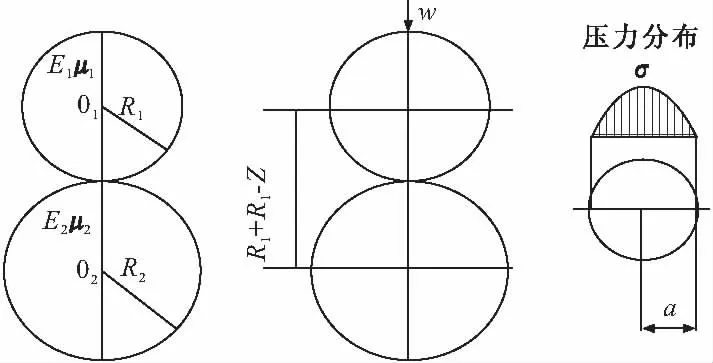
图1 两球体之间的赫兹接触

两球体受载接触面积的中心到任意半径距离r处的压应力σr为：

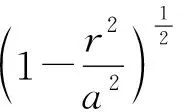
(3)

即当压应力不超过材料屈服应力时，其最大压应力位于接触圆的中心，而边缘(r=a)应力降至零，其沿接触圆直径的压力分布[6]如图1所示。

最大压应力：

(4)

即当两弹性体相互挤压时发生弹性变形，接触正应力呈椭球状分布。由此得到启发：当预应力束张拉时，与混凝土在弯曲孔道处相互作用产生弹性挤压变形，接触正应力呈中间大、两边小的趋势。而现行桥梁规范中预应力束与弯曲孔道间接触正应力与弹性接触理论中接触应力的分布有明显差异，其示意如图2所示。

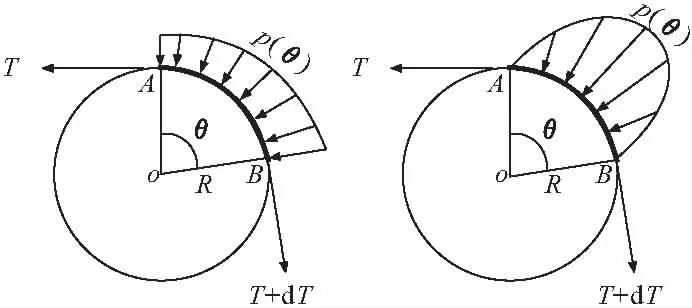
图2 现行设计理论与弹性理论接触应力分布示意图

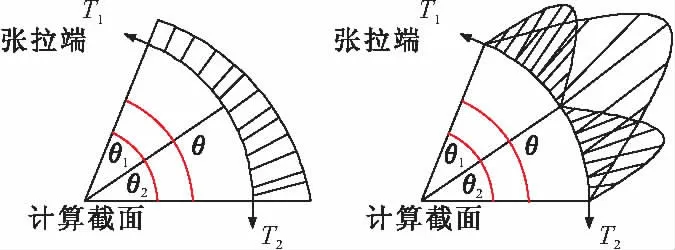
图3 连续与非连续弯曲孔道接触应力分布示意图

其次，对于接触夹角θ相等的连续与非连续弯曲孔道，其接触应力分布亦有明显区别，其示意如图3所示。为了说明弯曲孔道各夹角相加的不合理性，通过试验测试了张拉过程中钢丝绳与摩擦轮间的摩擦力矩[7，8]。

图4所示的试验装置，可用来测定张拉过程中预应力筋与混凝土在弯曲孔道处的摩擦阻力。图中摩擦轮半径R=173 mm，钢丝绳与摩擦轮接触面间的夹角为θ；轮缘表面粘贴一层薄的橡胶以增大摩擦，其与混凝土构件不同之处仅为摩擦系数μ的取值。当顺时针向转动摩擦轮时，钢丝绳与摩擦轮间产生相对滑动；在给定张拉力T下，显然有T>T′；在不同的T和不同的夹角θ下，由力传感器可测得相应状态下拉力T′的大小，从而可计算出钢丝绳与摩擦轮间的摩擦力矩

Mf=TR-T′R

(5)

图4 试验装置

按非连续弯曲孔道各夹角之和与连续弯曲孔道夹角相等的情况，将试验分为3个工况。对图5所示的连续弯曲孔道与非连续弯曲孔道的情形，有θ=θ1+θ2。在模拟非连续弯曲孔道各个角度的初始拉力时，在同一工况下，θ角所对应的初始拉力T与θ1角对应的初始拉力T1相等；而θ2角所对应的初始拉力T2与θ1角末端张拉力T1′相等(相当于将一连续弯曲孔道人为地分为两段)。对于多个非连续弯曲孔道，各个角度对应的初始拉力依此类推。

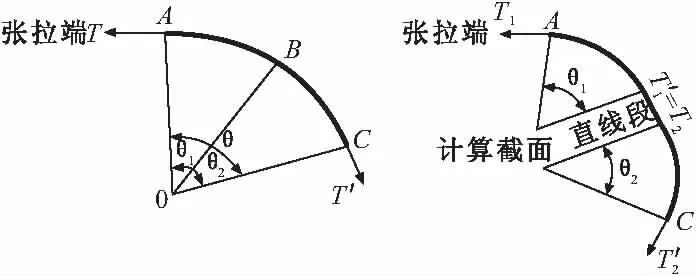
图5 弯曲孔道钢束张拉力

不同工况下，按不同张拉力、同一夹角θ与其分角之间的关系，表1给出了弯曲孔道摩擦力矩的试验结果。

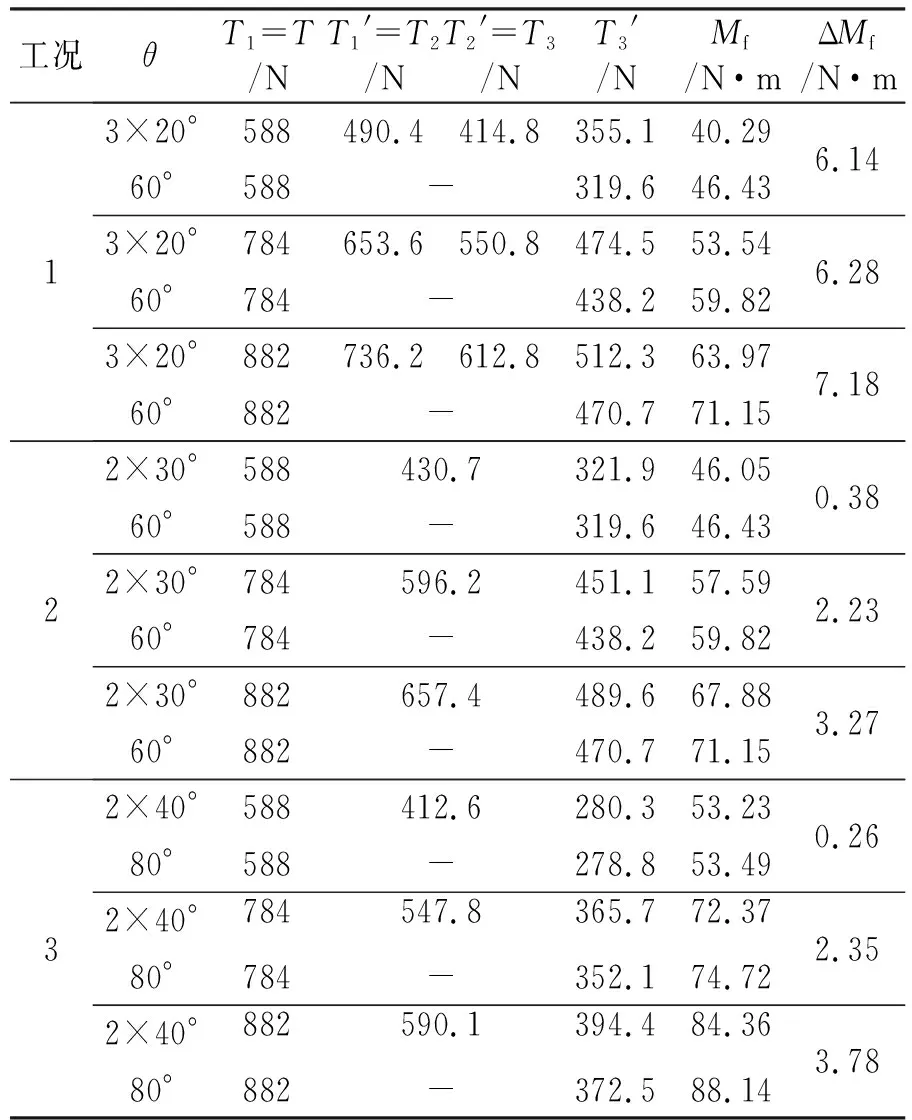
表1 不同工况不同张拉下的摩擦力矩

弯曲孔道，表明本文按弹性理论接触应力呈椭球分布的假设基本合理。

同时，许多混凝土结构中的预应力长束在设计张拉力作用下，实际伸长量严重不足，反映出式(6)不能很好地描述预应力束张拉的变化规律。

(6)

其中Δl为预应力束延伸量(mm)，E为预应力束弹性模量，其余参数同上。

为了说明预应力长束伸长量不足，以武咸公路改造工程为例。此工程部分桥梁为预应力混凝土箱梁结构。为了解混凝土箱梁顶板横向预应力束的张拉效果，对预应力束张拉过程中的应力变化进行了测试[9，10]。

取任一预应力束为研究对象，在其上沿纵向粘贴应变传感元件，其布置如图6所示。在预应力索张拉过程中，分别测试出对应点的应变值，从而推算出预应力索的预应力损失状况。

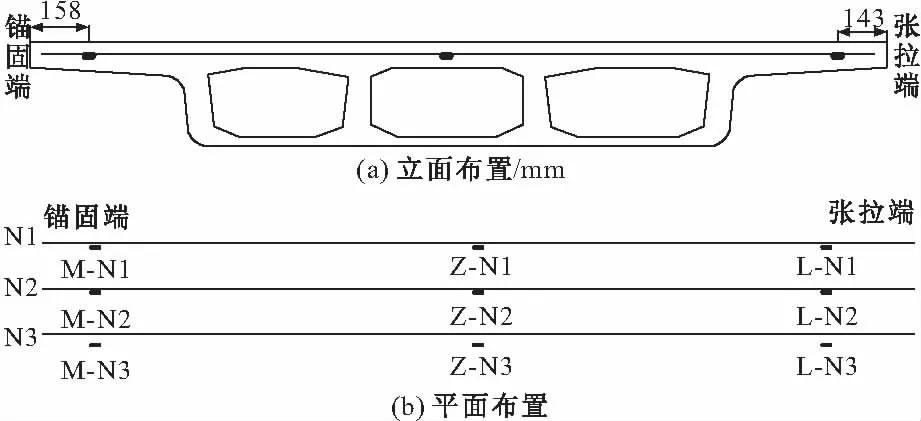
图6 应变传感器布置示意图

三束预应力钢绞线张拉应变测试平均值见表2。

表2预应力束应变测试数据

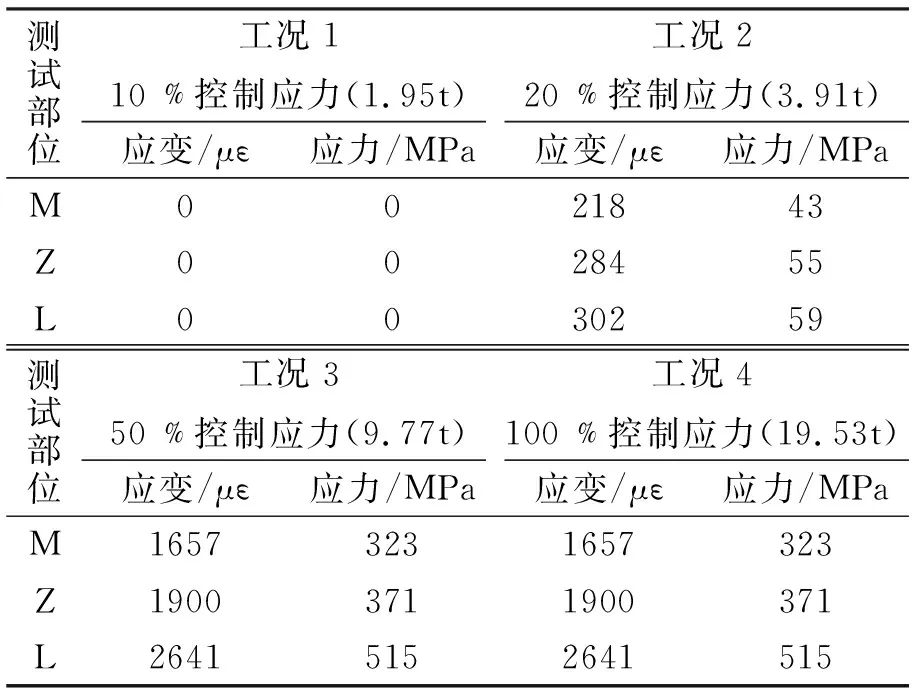
测试部位工况110﹪控制应力(1.95t)应变/με应力/MPa工况220﹪控制应力(3.91t)应变/με应力/MPaM0 0 218 43 Z0 0 284 55 L0 0 302 59 测试部位工况350﹪控制应力(9.77t)应变/με应力/MPa工况4100﹪控制应力(19.53t)应变/με应力/MPaM1657 323 1657 323 Z1900 371 1900 371 L2641 515 2641 515

注：预应力钢绞线弹性模量E=1.95 GPa。

从表2可知，各应变测试断面的应变值随张拉力的增大基本呈线性增长，分别如图7和图8所示。

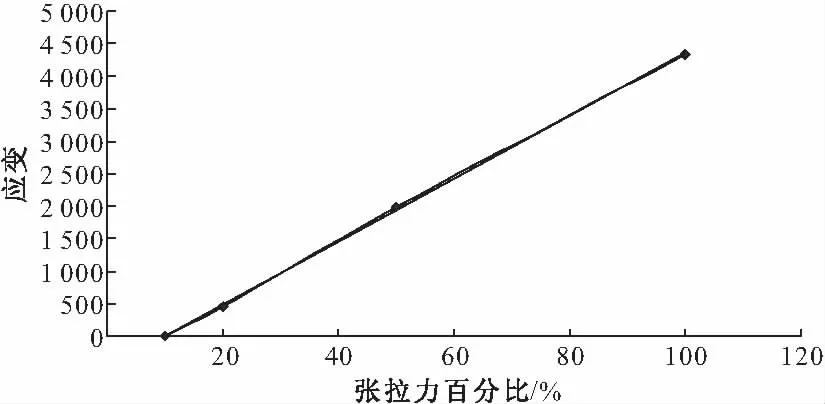
图7 锚固端应变变化

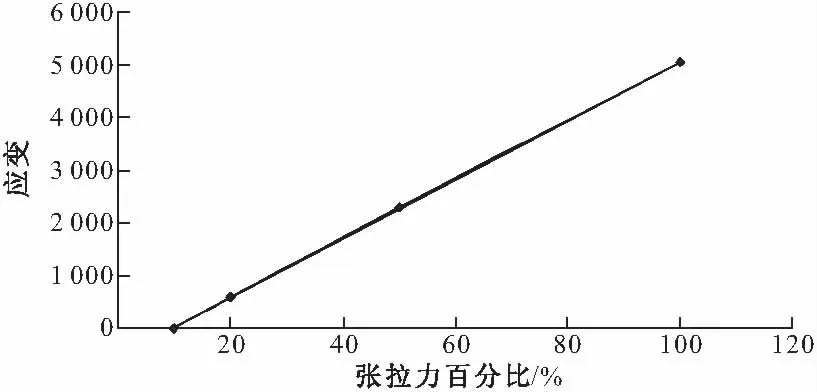
图8 中部应变变化

依据图7和图8所示的线性关系，可推出各应变测试断面设计荷载下的应变值，见表3。

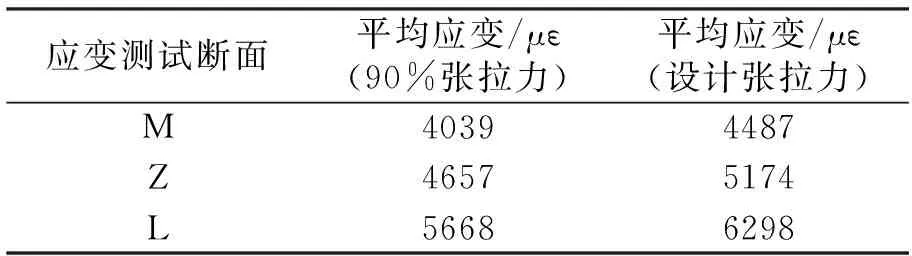
表3 设计张拉力下各测试断面应变值

设计张拉力下，各应变测试断面应力值与理论值比较见表4。

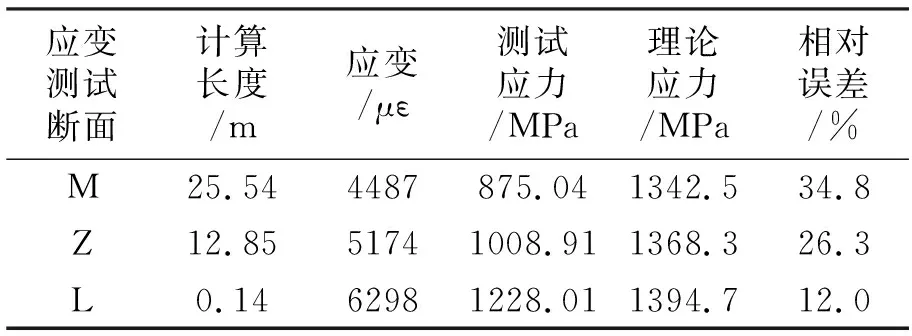
表4 设计张拉力下各控制断面应力值比较

在设计张拉力作用下，应力实测值与理论值相对误差较大，表明预应力钢绞线的预应力损失值较理论计算值要大；且离张拉端越远，其偏差越大。该结果和目前绝大多数预应力混凝土钢绞线张拉的情况一致。

根据库仑(Coulomb)摩擦定律，预应力束与弯曲孔道间相对滑动摩阻正比于接触正压力，故由弯曲孔道摩阻引起的预应力损失依赖于接触正压力的分布；不同的接触正压力，将产生不同的摩擦阻力,且与接触物体间的曲率半径和弹性模量有关；预应力束对弯曲孔道混凝土将产生很大的径向压力，使得混凝土结构局部变形，从而改变了接触面处的曲率半径R，影响径向压力p的分布规律。式(1)在推导过程中存在着如下问题：①视混凝土结构为刚体，忽视了材料物性因素和接触物体弹性变形对接触应力的影响；②仅仅利用了接触物体间的静力平衡关系，其接触应力p取决于张拉力T和弯曲半径R；在不考虑几何方程、物理方程和边界条件的情况下，不可能得到接触正压力的分布关系；③当预应力束与弯曲孔道无相对滑动时(或不计摩擦)，管道内壁的径向压力p(θ)在接触面上呈均匀分布。

2 接触正压力分布假设

由赫兹(Hertz)接触理论得到启示，预应力束与弯曲孔道间的接触正应力分布比较复杂，在目前无法得到其解析式的情况下，分别假设接触正应力为均匀分布、余弦分布、抛物线分布和椭圆分布，利用静力平衡关系识别其相关参数。各假设接触压力分布形式如图9～12所示(其中T为张拉力,p0为最大接触压力)，其接触压力计算式见表5。

表5 各假设接触压力分布形式下的接触压力计算式

注：接触正压力分布的假设均不计摩擦。

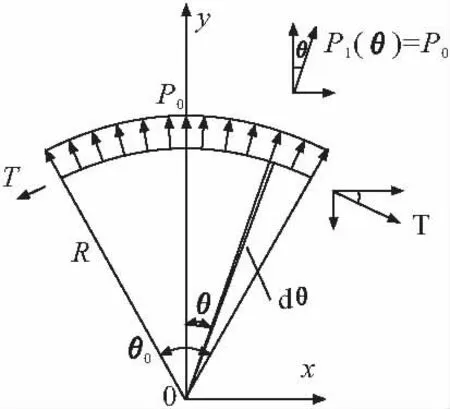
图9 均匀分布正压力

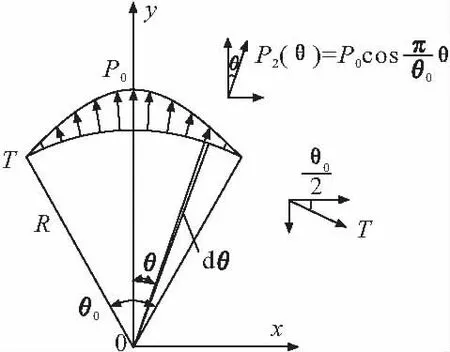
图10 余弦分布正压力

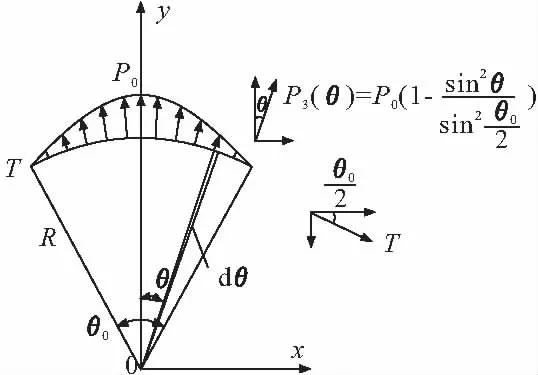
图11 抛物线分布正压力

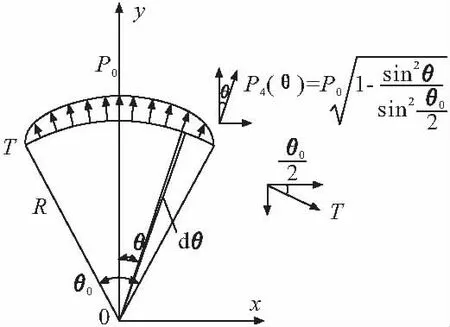
图12 椭圆分布正压力

3 不同接触压力分布下的摩阻损失

为了比较不同接触压力分布下的摩阻损失，取一微段预应力束分离体(图13)为研究对象。并假定：①在预应力束双边对称张拉施加预应力，始端张拉力为T0；②弯曲孔道摩阻力与接触正压力遵循库仑摩擦定律，μ为常量，且物体间产生相对滑动；③曲率半径R变化时对预应力弯曲孔道接触应力假定分布没有影响。

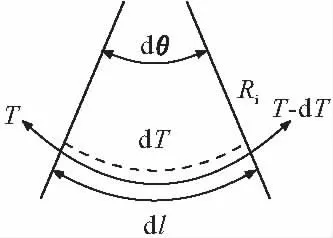
图13 预应力束微段受力示意图

3.1 摩阻损失计算式

弯曲孔道在各假定接触应力分布下，由图13所示预应力束受力图建立静力平衡方程

dT=-μpidl=-μpiRdθ

(7)

将表5推导的接触压力分布公式代人，且由张拉端边界条件T=T0得c=lnT0。那么，可得均匀分布接触应力下的摩阻损失为

(8)

同理，余弦分布接触应力下的摩阻损失为

(9)

抛物线分布接触应力下的摩阻损失为

(10)

椭圆分布接触应力下的摩阻损失为

(11)

3.2 摩阻损失比较

对于不同的弯曲夹角θ0，可计算各假定接触压力分布下的摩阻损失；并分别与均匀分布接触压力下的摩阻损失进行比较，结果见表6。

3.3 数据分析

(1)随着弯曲角度的增大，各分布接触压力摩阻损失均呈上升趋势。

(2)均匀分布接触压力下的摩阻损失大于其它分布接触压力下的摩阻损失。然而，这与实际结构预应力摩阻损失过大相矛盾。其结果表明：影响预应力摩阻损失的因素有许多，比如：预应力束与混凝土在弯曲孔道处的摩擦系数μ取值是否合适；当预应力束张拉力很大时，接触体间部分材料产生挤压塑性变形，在此情况下的库仑摩擦定律是否仍然适用等。

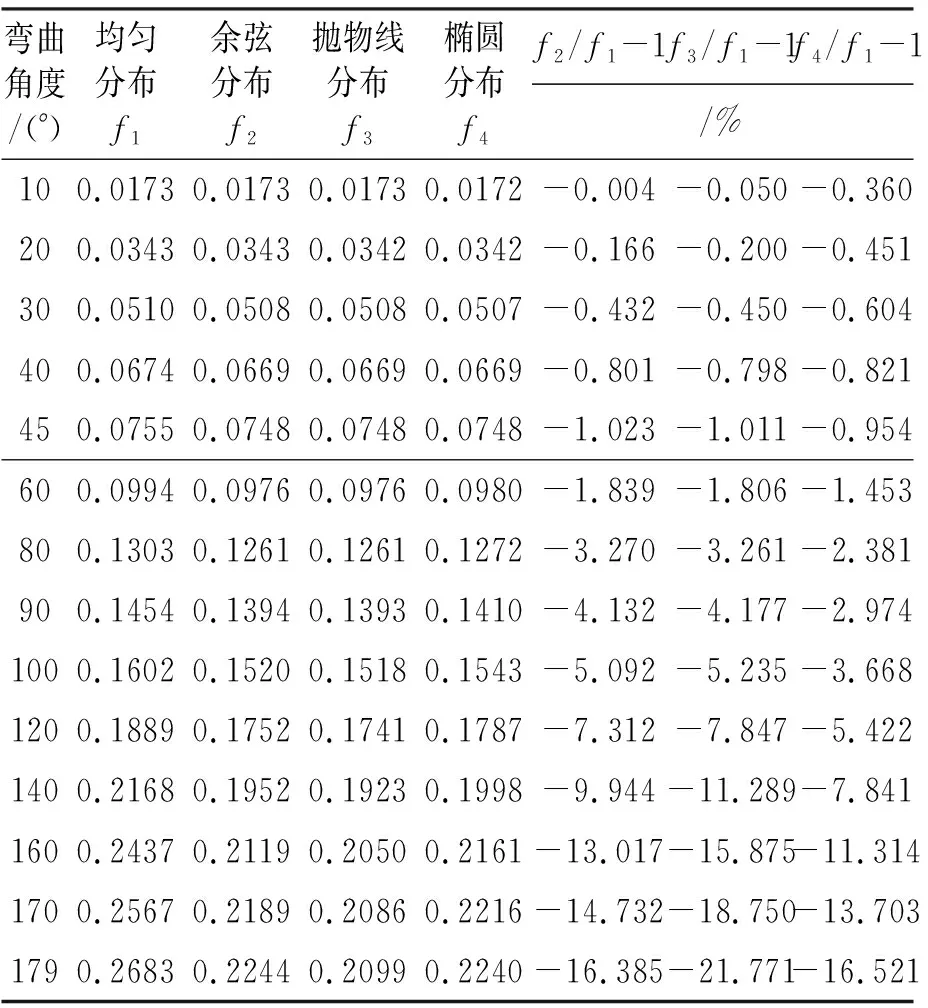
表6 各假定接触压力分布下的摩阻损失

注：(1)令各假设接触压力分布函数情况下的μ=0.2,T/A=1；(2)由于椭圆分布摩阻损失无解析式，表中的f4为数值解。

4 结 论

预应力混凝土构件中，实际结构的预应力摩阻损失往往大于理论计算值，致使混凝土构件变形过大、跨中下挠或开裂失效。本文就预应力束与弯曲孔道间的接触应力分布形式及其所引起的预应力损失进行了初步研究，得到如下结论：

(1)对于非连续分布弯曲孔道，现行规范有效预应力计算式中θ值表述为张拉端至计算截面曲线孔道部分切线夹角绝对值之和是不合适的，各非连续弯曲孔道有效预应力不能等同于相同夹角的连续弯曲孔道所产生的摩阻损失，而应该分别计算；

(2)实际混凝土连续梁桥、连续刚构桥预应力长索在设计张拉力作用下，实际伸长量严重不足，反映出现行规范预应力束伸长量计算式不能很好地描述预应力束张拉的变化规律。

对于大跨度预应力混凝土连续梁桥、连续刚构桥的设计，预应力摩阻损失至关重要。然而，导致结构预应力损失的因素有很多：结构预应力摩阻损失计算表达式不合理；预应力束与混凝土材料间摩擦系数取值偏小；当预应力束张拉时，接触体间产生较大的挤压变形，库仑摩擦定律是否仍然适用等，都有待作深入的探讨和研究。

[1] 张世辉.大跨预应力混凝土连续刚构桥跨中持续下挠原因分析及施工控制实践[D].成都：西南交通大学，2007.

[2] 李准华,刘 钊.大跨度预应力混凝土梁桥预应力损失及敏感性分析[J].世界桥梁，2009,(1):36-39.

[3] 李伟兴，黄鼎业，李德章.超长预应力束孔道摩擦的探讨及应用[J]．结构工程师，1999,(3):14-17.

[4] JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[5] 徐芝纶.弹性力学[M].北京：高等教育出版社，1990.

[6] (英)霍林J.摩擦学原理[M].上海交通大学摩擦学研究室译.北京:机械工业出版社,1981.

[7] 张开银,郭志伟,顾津申.PC弯曲孔道摩阻预应力损失试验与分析[J].中外公路,2010,30(4):145-149.

[8] Zhang Kai-Yin,Cheng Chen. Analysis on Prestress Loss Caused by Friction in Curved Duct in The Design of Prestressed Concrete Structure[C]∥The 4th International Symposium on Lifetime Engineering of Civil Infrastructure. Beijing:Science Press, 2009:701-705.

[9] 梁勇旗,张文胜,门小雄,等.钢绞线预应力张拉中有关问题探讨[J].公路交通科技(应用技术版)，2006,(6):126-128.

[10] 严登彩.大跨径连续刚构桥预应力摩阻损失研究[J].交通科技，2008,(7):4-6.