一种适用于任意复杂结构的曲六面体网格生成算法
2018-05-23盛天爽
盛天爽*
一种适用于任意复杂结构的曲六面体网格生成算法
盛天爽*
(南京师范大学附属中学高二(4)班,江苏南京,210094)
曲六面体网格自动生成是时域谱元法发展的瓶颈问题。本文采用基于体基函数的协变投影算法,将一个10节点曲四面体单元分解为四个20节点曲六面体单元,从而形成一种适用于任意复杂结构的曲六面体网格生成算法。使用该算法能够将曲四面体单元均匀分割,且确保新形成的曲六面体单元的翘曲最小。典型算例表明,使用该算法建立的曲六面体离散模型,完全满足时域谱元法的计算精度要求。
网格自动生成;曲四面体;曲六面体;协变投影
引言
在计算电磁学领域,时域谱元法(SETD)是一种较为新型的数值仿真算法。这种算法不仅具有类似于FDTD算法的显式求解格式,而且随着算法中所使用的正交基函数阶数的增加,其计算精度呈指数增长,即具有谱精度特性[1]。在时域谱元法中,通常使用具有20个节点的曲六面体单元作为基本离散单元,以确保仿真计算的谱精度性,但是受到六面体拓扑结构的限制,实现可靠、高质量的曲六面体网格自动生成一直是时域谱元法发展的瓶颈问题。为了绕开这一问题,人们只能使用分区域离散的方式建模[2],对复杂结构使用曲四面体建模,其余部分采用曲六面体建模。但这样的操作不仅增加了算法的复杂性,而且也破坏了算法所具有的全局显式求解格式,降低了算法的效率。
事实上,人们很早就认识到使用曲六面体建模具有空间逼近度高、计算精度高的特点,也设计了很多种方法来实现曲六面体网格的自动生成,但相比能适用于任意复杂结构的曲四面体来说,实现曲六面体网格的自动生成还没有通用的方法[3]。目前通常使用的方法主要有单元映射法[4]、栅格分解法[5]、四面体转换法[6]、逐层推进的波前法[7][8]等等。其中,单元映射法虽然最易实现,却不适用于复杂三维结构的离散。栅格分解法只能生成规则化网格,且边界单元的质量较差。逐层推进的波前法生成的六面体网格质量最优,但其实现难度最大,易产生单元间的裂缝以及形状尺寸不合理的单元。
四面体转换法是目前最具有通用性的六面体自动生成算法,该算法首先使用直四面体建模,在此基础上,再将每个直四面体单元分离为4个直六面体单元。但使用直四面体建模时,往往需要很大的剖分密度才能保证对复杂结构的拟合精度,从而导致生成更多的直六面体单元,极大增加了未知量的个数。事实上,使用具有曲边和曲面的高阶离散单元可以更好的拟合复杂结构,并且能避免过大的剖分密度。于是国内有学者提出了采用从曲四面体单元中分离出六面体单元的算法[9],该算法在区分曲面和直面的基础上,使用面基函数,通过空间映射得到曲四面体的曲面形心坐标,再根据常规的四面体转换法,获得4个准曲六面体单元。该算法操作起来较为繁琐,且形成的准曲六面体单元中即包含曲面,又包含直面,并非常规的包含20个几何节点的曲六面体单元,因此无法直接用于时域谱元法。
本文对该算法做了改进,不必区分曲四面体中的曲面和直面,直接使用体基函数,通过谐变投影映射方式,在一个10节点曲四面体单元中获得4个20节点曲六面体单元。
2 算法原理
笛卡儿坐标系下的二次曲面四面体单元包含10个几何特征节点,分别定义于四面体的4个顶点和6条棱边的中点,通常称为10节点曲四面体单元,如图1(a)所示。
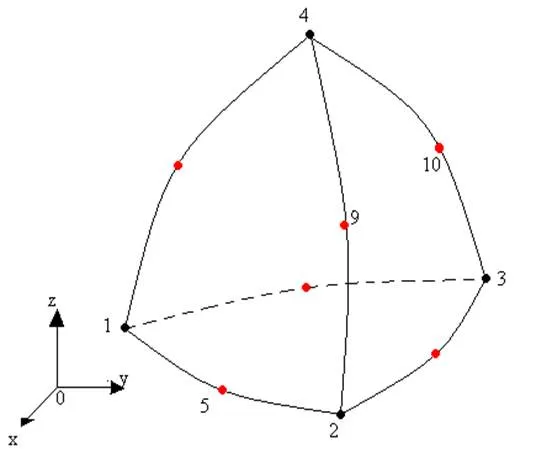
图1 10节点曲四面体单元

图2 参量空间的的直角四面体单元
根据协变投影原理,真实空间中的10节点曲四面体单元与参量空间的直角四面体单元之间的空间映射关系为

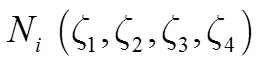
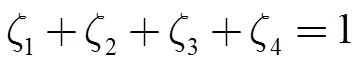
显然,在参量空间中,直角四面体单元里任意一点的坐标由相应的4个参变量唯一确定。据此,可以将任意一个曲四面体单元投影为体坐标系中的标准直角四面体单元,如图2所示。其中,直角顶点位于坐标系原点,三条直角棱边分别位于三坐标轴,边长均为1。
上述形函数N的具体表达形式为
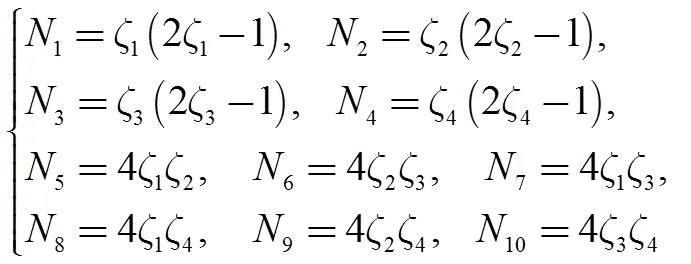
将式(3)带入空间映射关系式(1),即可以获得体坐标系中直角四面体单元内任意一点在相应曲四面体单元中的笛卡尔坐标。基于这一原理,我们可以先在体坐标系中将一个标准的直角四面体单元分裂为四个直六面体单元,如图3所示。
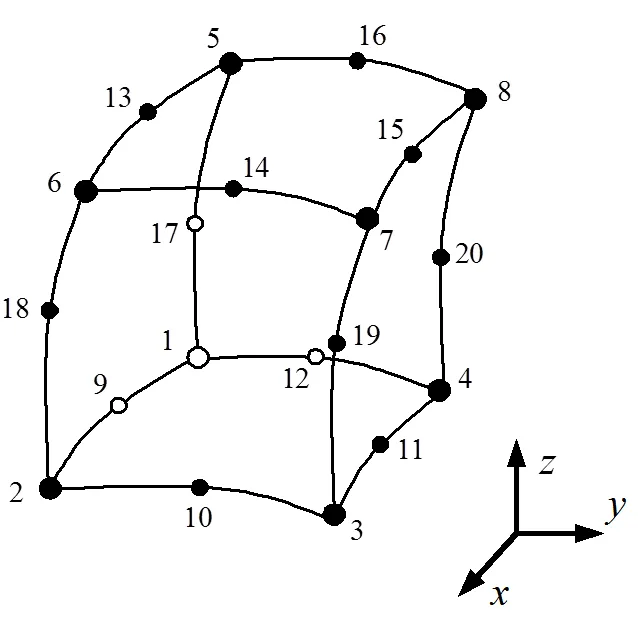
图4 20个几何节点的曲六面体单元
其中,编号1~10的点对应于曲四面体的10个几何节点,编号11的点为体中心点,编号12~15的点分别为4个面的形心。将相应各点连接起来,便可以在一个直四面体中获得4个直六面体。表1列举了将一个四面体单元分裂为4个六面体单元时,各六面体中8个顶点的序列分布。
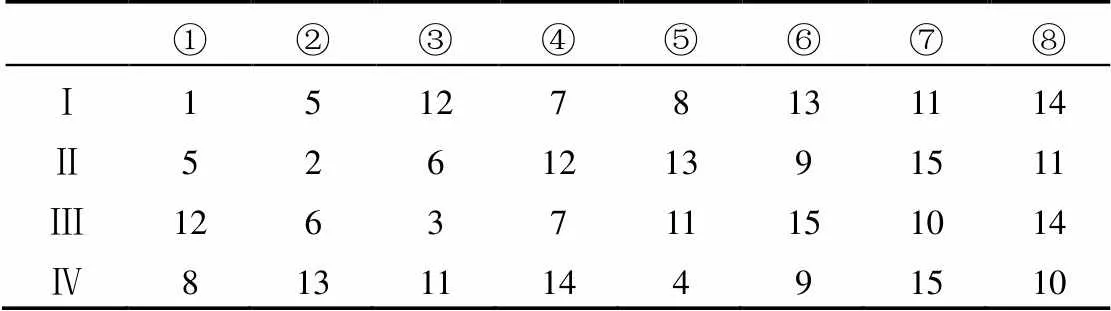
表1 四个六面体的顶点编号
以上操作在体坐标系中进行,最后获得4个直六面体单元。但曲六面体元的几何节点有20个,分别位于8个顶点和12条棱边的中点,如图4所示。因此,我们还需要在体坐标系中,针对新形成的4个直六面体单元,分别按照曲六面体20个几何节点的分布规律,重新建立相应几何点的体坐标。最后,再通过协变投影,在真实空间获得4个曲六面体单元。
在本文介绍的算法中,将体坐标系中的直六面体单元映射到真实空间时采用了协变投影,因此得到的曲六面体单元的翘曲最小。并且,在体坐标系中定义4个六面体的分界点时采用的是体积变量,因此可以准确控制曲四面体的均匀分割。例如,四面体的中心点(图3中编号为11的点),可以直接定义为(1/4, 1/4, 1/4, 1/4)。通过协变投影,该点在相应曲六面体中也必然位于体积均分的中心点位置。根据这一原则,我们给出图3中15个几何点的体坐标定义,如表2所示。
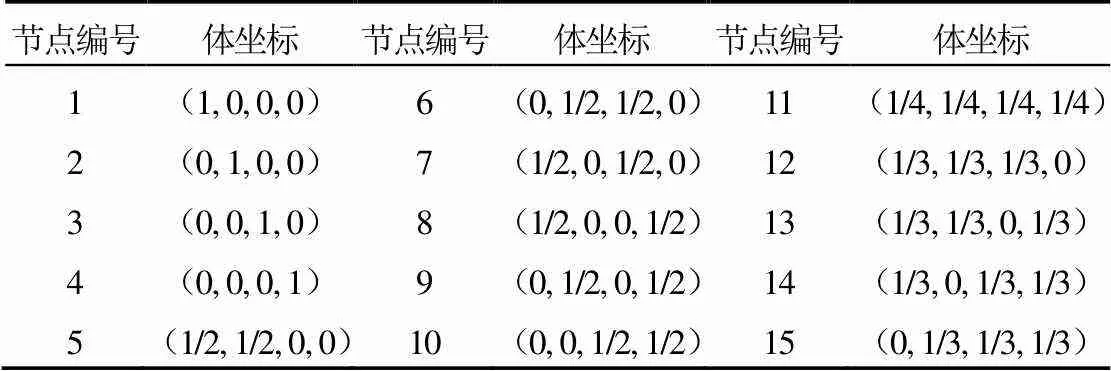
表2 图3中15个几何点的体坐标定义
根据表2可以确定体坐标系中每个直六面体的8个顶点坐标。在此基础上,计算每条棱边的中点坐标,从而获得所有20个节点的体坐标。带入式(1),即可求得相应曲六面体单元的20个几何节点的真实坐标。
2 算例
使用协变投影获得的曲六面体单元具有最小翘曲,因此可以确保使用该算法所获得的曲六面体单元在用于时域谱元法时计算的准确性,下面通过一个简单的算例加以验证。一个半径为1米的球形金属谐振腔,利用商业电磁仿真软件HFSS,得到三个最低谐振频率分别为132.089MHz、186.439MHz、216.551MHz。在ANSYS软件中建立模型,并且分别使用10节点的曲四面体单元和20节点的曲六面体单元对模型进行离散。使用曲六面体离散时,需要先对球体进行合理切割,以确保各子区域的空间拓扑结构满足曲六面体离散的要求,剖分后获得448个曲六面体单元。使用曲四面体离散时,对模型无需特殊处理,直接离散后获得72个曲四面体单元。再根据本文算法,将这72个曲四面体离散为288个曲六面体,计算出每个曲六面体单元中20个几何节点的坐标,并对其进行全局编号。依据两种不同离散方式建立的模型,使用时域谱元法分别计算该球形谐振腔的谐振频率,仿真结果如图5所示。
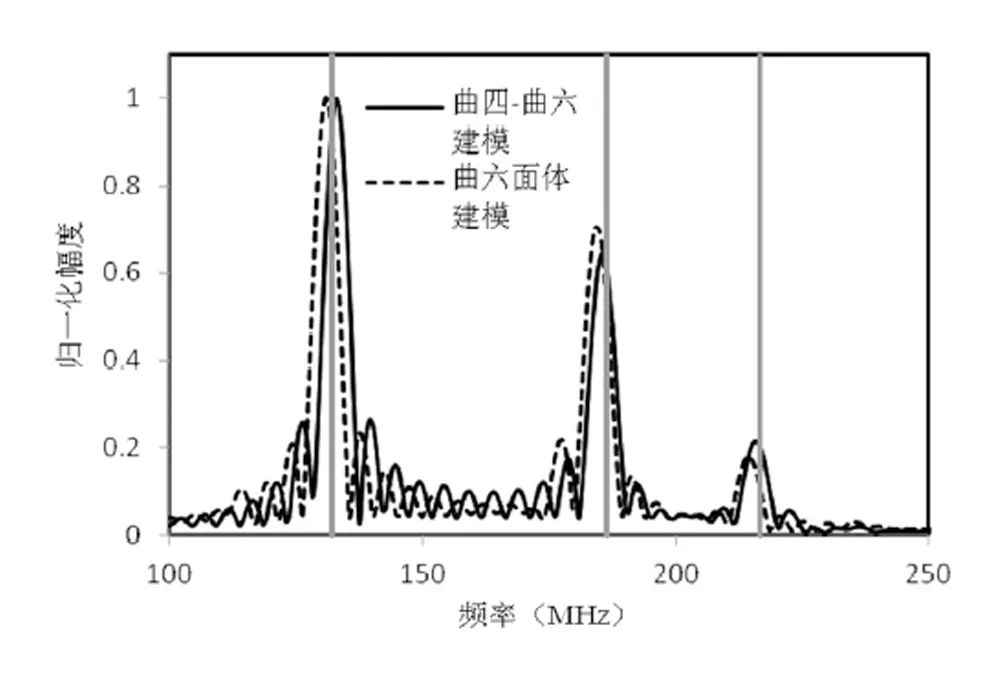
图5 半径1米球形谐振腔的三个最低谐振频率
图中,灰色竖线为HFSS仿真得到的三个最低谐振频率值;黑实线为使用曲四面体转换曲六面体方法建模时,仿真所获得的谐振频率值;虚线为直接使用曲六面体建模时,仿真所获得的谐振频率值。显然,使用本文算法所获得的曲六面体离散模型,完全满足时域谱元法的计算精度要求。
3 结束语
使用时域谱元法进行电磁仿真时,实现复杂计算模型的曲六面体网格离散是个难题。本文对常规的“四面体转换法”做了改进,根据协变投影原理,采用体基函数映射的方式,在一个10节点曲四面体单元中获得4个20节点曲六面体单元。实际操作中,由于将体坐标系中的直六面体单元映射到真实空间时采用了协变投影,因此所获得的曲六面体单元具有最小翘曲。同时,在体坐标系中使用体积变量定义4个六面体的分界点,可以更准确地控制曲四面体的均匀分割。从给出的典型算例也可以看出,由于曲四面体适用于曲面拟合,因此在不降低计算精度的前提下,可以极大减少建模时所需要的离散单元数量,并最终减少曲六面体单元的数量,从而减少未知量,加快仿真速度。该曲六面体网格自动生成算法具有很强的通用性,适于任意复杂结构的建模。
[1] Joon-Ho Lee, and Qing H. Liu, A 3-D Spectral-Element Time-Domain Method for Electromagnetic Simulation, IEEE Trans. on M.T.T., 2007, 55(5): 983-991.
[2] Qiang Ren, Luis E. Tobón, Qingtao Sun, Qing Huo Liu, A New 3-D Nonspurious Discontinuous Galerkin Spectral Element Time-Domain (DG-SETD) Method for Maxwell’s Equations, IEEE Trans. on A.P., 2015, 63(6): 2585-2594.
[3] 吕军, 王忠金, 王仲仁, 有限元六面体网格的典型生成方法及发展趋势, 哈尔滨工业大学学报,2001, 33(4): 485-490.
[4] 蒋浩民, 刘润广, 王忠金, 等, 基于映射法的三维有限元网格自动划分, 塑性工程学报, 1998 , 5(3): 27-31.
[5] TEKKAYAAE. Fully automatic simulation of bulk metal forming processes. Proc NUMIFORM' 98. Rotterdam: Netherlands, 1998.
[6] G Xie, JAH Ramaekers, Graded mesh generation and transformation. Finite Elements in Analysis and Design, 1994, 17(1): 41-55.
[7] TD Blacker, RJ Meyers, A 3-D hexahedral mesh generation algorithm. Engineering with Computers, 1993, 9(2): 83-93.
[8] 尚菲菲, 甘洋科, 郭宇飞, 刘剑飞, 基于片分割的六面体网格生成方法, 计算机辅助设计与图形学学报, 2017, 29(4): 662-669.
[9] 左旭, 卫原平, 陈军, 阮雪榆, 三维六面体有限元网格自动划分中的一种单元转换优化算法, 计算力学学报, 1999, 16(3): 343-348.
An Algorithm for Generating Curved Hexahedron Mesh for Arbitrary Complex Structures
SHENG Tianshuang*
(High School Affiliated to Nanjing Normal University, Grade 2, Class 4, Jiangsu Nanjing, 210094, China)
Automatic generation of curved hexahedron mesh is a bottleneck in the development of spectral-element time-domain method. In this paper, the covariant projection algorithm based on volume basis function is adopted to decompose a 10-node curved tetrahedron element into four 20-node curved hexahedron elements. Thus, a curved hexahedron mesh generation algorithm suitable for arbitrary complex structures is proposed. Using this algorithm, the curved tetrahedron element can be partitioned evenly and the minimal warping can be ensured for these new hexahedron elements. The typical example shows that the curved hexahedron model established by this algorithm fully meets the precision requirement of the spectral-element time-domain method.
Automatic mesh generation; Curved tetrahedron; Curved hexahedron; Covariant projection
TP39
A
10.19551/j.cnki.issn1672-9129.2018.01.010
1672-9129(2018)01-0022-03
盛天爽. 一种适用于任意复杂结构的曲六面体网格生成算法[J]. 数码设计, 2018, 7(1): 22-24.
SHENG Tianshuang. An Algorithm for Generating Curved Hexahedron Mesh for Arbitrary Complex Structures[J]. Peak Data Science, 2018, 7(1): 22-24.
2017-11-01;
2018-01-05。
盛天爽(2001-),男,江苏南京,南京师范大学附属中学高二(4)班,学生。E-mail: shengyij@.edu.cn
