移动式加载系统中运送动载对支撑架的影响
2011-01-24郑俊杰
余 舜, 张 娟, 王 平, 郑俊杰
(1. 华中科技大学 土木工程与力学学院, 湖北 武汉 430074; 2.中国一冶集团有限公司, 湖北 武汉 430081)
传统的砂袋加载预压桥梁支撑架的方法存在一些弊端,如雨天砂袋吸水,导致砂袋自重增加,产生超载;砂袋计量不准确,加载试验不规范等,这些弊端会给加载预压试验的安全留下隐患。本文所研究的可移动式预制构件加载系统是一种新型的桥梁加载预压试验系统。此方法的创新在于:首先用预制构件作为加载材料,根据箱形梁各部位预压荷载大小的不同,可相应选择不同尺寸、不同重量的预制构件,这样就不会受到下雨增加自重的影响,如此荷载的计量会更加准确,同时也使施工更加安全、高效;其次通过在桥梁一端使用小型吊车将预制构件吊上轨道,然后使用运输小车调运预制构件到位,如图1所示。这样就不会占道施工,并且可以随时施工作业,可以大幅度缩短工期;另外,相比传统砂袋加载预压方法,新型加载预压方法中使用的预制构件可以重复使用,符合循环、低碳、节能环保等方面的要求。
现有的对桥梁支撑架的研究大多是针对桥梁支撑架在施工过程中的静力分析,目前对桥梁支撑架结构分析的计算方法主要分为三大类:无侧移刚架法、铰接计算法和半刚性节点法。由于无侧移刚架法无侧向水平位移,因而其变形条件只能在刚结点发生转角,所以其结果与铰接点的结果相同[1]。铰接计算法假定扣件的连接为无滑移、无刚接影响,并认为横杆在框架结构体系中是不受力作用的,只是起到了减少立杆有效长度的作用[2]。按半刚性连接分析的理论值与实验值比较接近。因此,扣件的转动刚度对保证理论分析的准确性十分重要。半刚性节点方法认为支撑架是由纵向、横向水平杆组成的多层多跨空间框架结构,节点由于采用扣件连接而具有半刚性且抗扭转刚度与扣件质量和拧紧程度密切相关,半刚性假设比较符合扣件的实际情况[3~5]。

图1 新型加载试验照片
本文所研究的采用可移动预制构件对桥梁支撑架进行加载试验是一种新型加载试验方法,该方法需要小车运输预制构件,运输预制构件过程中运输小车对桥梁支撑架将产生额外的运动荷载影响,之前没有相关研究。为了保证施工安全,需要考虑运输小车对桥梁支撑架的动力荷载影响,并对附加的动力荷载作用规律进行分析。本文采用ANSYS对可移动式预制构件用于桥梁支撑架的加载过程进行数值模拟,研究了小车在不同运送速度条件下桥梁支撑架的动静力特性,并着重对比分析了支撑架杆件动静力响应峰值之间的差别。
1 数值模型
1.1 单元类型、材料参数及网格划分
本文采用ANSYS进行数值模拟分析,计算选取桥梁支撑架为研究对象,计算范围为沿桥梁支撑架纵向长度27 m,横向宽度为18 m,桥梁支撑架高度为18 m。支撑架与其扣件间的连接作用较复杂,本模型中假设桥梁支撑架的连接为刚性连接,故模型中采用BEAM4单元进行模拟;为了考虑支撑架和下部土体的相互作用带来的影响,支撑架底部设置LINK8单元来模拟;支撑架上部分别铺设钢模板和松木板,计算时将其等效为一个整体箱梁模板,采用SOLID45单元进行模拟,材料参数采用复合法计算得到;采用BEAM4单元来模拟箱梁模板上的小车运送轨道。材料的物理力学参数见表1,表中LINK8仅为模拟支撑架和土体的相互作用,故没有密度。

表1 材料物理力学参数
模型的边界条件为:在整个模型底部设置x、y、z三个方向约束,在支撑架底部设置x、y方向约束。整个模型网格划分如图2所示,共有61432个单元,23064个节点。

图2 网格划分
1.2 运送荷载的确定及施加方法
相对于传统加载方法,桥梁支撑架可移动式加载系统的特点在于:在加载过程中需要运输小车运送预制构件。因此对于这种新型的可移动式加载方法来说,在根据相关荷载分布资料计算静力荷载的基础上,还需要分析动力荷载的影响程度。
目前关于加载小车的动力荷载的确定方法尚不明确,也未见相关的试验结果及理论研究成果。因此,本课题在确定加载小车的动力荷载时,只能借鉴列车动荷载的确定方法。用一个激振力函数来模拟列车荷载,其表达式为[6]:
F(t)=P0+P1sinX1t+P2sinX2t+P3sinX3t
(1)
实际上运输小车形成的冲击动力荷载不同于多轮组列车荷载。对于多轮组列车荷载而言,轨道上的某一个节点会连续受到列车车轮的冲击作用;但对于运输小车形成的动力荷载而言,在一次运输过程中轨道上的某一个节点只会受到一次类似于脉冲式的冲击作用。因此,在实际模拟过程中,需要依照小车实际的运行速度,对轨道上的节点依次施加图3所示的脉冲式的冲击荷载。图中0时刻表示小车前轮到达目标节点前一个相邻节点的时间;t1时刻表示小车前轮到达目标节点的时间;t2时刻表示小车后轮到达目标节点的时间;t3时刻表示小车后轮离开目标节点后一个相邻节点的时间。在上述脉冲式冲击荷载的确定过程中,采用了结构力学中外荷载等效节点力的求解方法,这样可以较为真实地模拟各个加载条件下桥梁支撑架的实际动力响应。
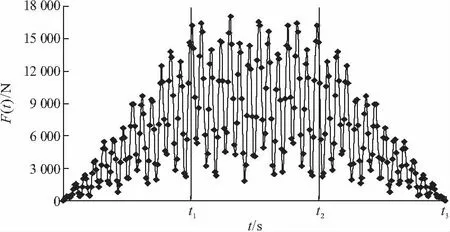
图3 在每个节点上施加的脉冲式的冲击荷载
由于支撑架、模板等均采用线弹性模型进行模拟,叠加原理是有效的。因此,本章的动力分析通过先计算得到各个加载条件下的静力计算结果,然后叠加动力响应结果,即可得各个加载条件下桥梁支撑架的实际动力响应。
在分析桥梁支撑架结构受到静力作用与动力作用时所采用的基本计算模型相同,只是所施加荷载不同。荷载的施加方式为将荷载平均施加到相应的节点,在动力计算中使用ANSYS瞬态求解器计算动力作用效应,并控制每个节点的脉冲式的冲击荷载时间t1、t2和t3。
1.3 分析工况及模拟过程
实际施工中有两层预制构件,分奇、偶车道分别运输,运输小车同时在加载模板上的奇数车道或偶数车道上调运预制块。如图4所示,本模型沿x方向共有11个车轨,10个车道,其中5个奇数车道,5个偶数车道,车轨从左至右编号依次为1~11。加载试验过程中所施加的预制构件共分为两层,分四次运送至箱梁模板上。施工顺序为:先堆放第一层的奇数车道,然后堆放第一层的偶数车道,接着堆放第二层的奇数车道,最后堆放第二层的偶数车道。

图4 分析模型整体示意
在动力分析中计算运输小车在不同速度下,不同动力加载工况对应的支撑架受力和变形情况。共计算分析了12种工况,其中前8个工况的小车速度为6 km/h,后四个工况的小车速度分别为2 km/h、4 km/h、8 km/h和10 km/h,各工况的详细说明见表2及其备注。

表2 模型计算工况
注:表格中的G、O分别表示奇数和偶数车道,1、2分别表示第一层和第二层车道,例如G1表示第一层奇数车道;k1~k15为车道的预制构件编号,具体编号位置如图4所示。
2 加载过程中运送动载的影响规律
由于杆件单元数量庞大,为了分析方便,重点选取几个特征横断面上的杆件单元分析受力、变形情况,如图5所示,分别选取1/4跨横截面和1/2跨横截面上的代号为A-H的杆单元进行分析,从图中可以看出各个重点分析杆单元的分布情况。
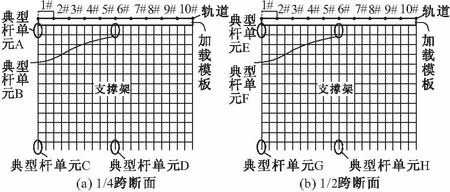
图5 数据分析中选取的重点分析杆件示意
2.1 典型杆件的轴力时程
图6、7分别给出了速度为6 km/h,工况6条件下1/2跨断面上典型杆件E、H的轴力时程曲线图。
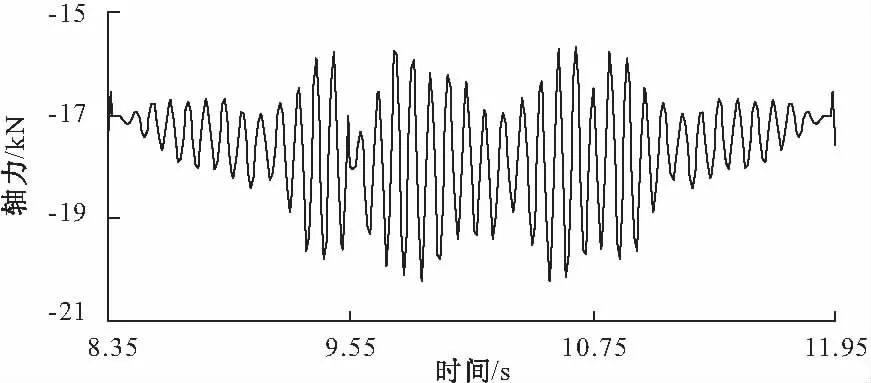
图6 典型杆件E的轴力时程曲线(v=6 km/h)
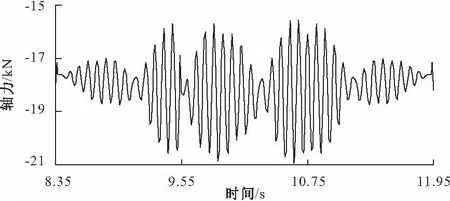
图7 典型杆件H的轴力时程曲线(v=6 km/h)
2.2 加载过程中典型杆件响应峰值
在表3中统计了速度为6 km/h时典型部位支撑架构件在整个工况时间内的最大轴力值(表中负号表示受压,正号表示受拉)。表4给出了速度为6 km/h时动静力响应峰值的差值占静力峰值的比例。
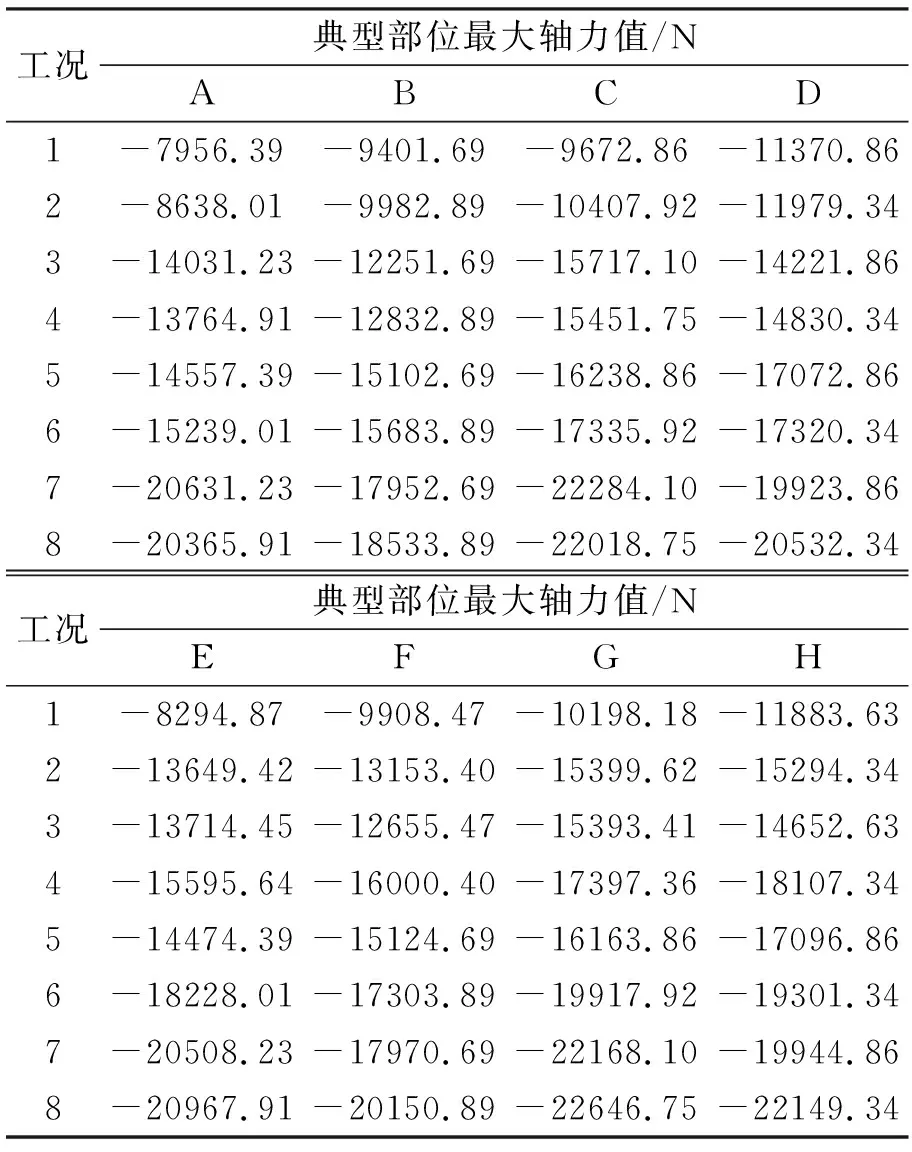
表3 典型部位支撑架构件最大轴力值
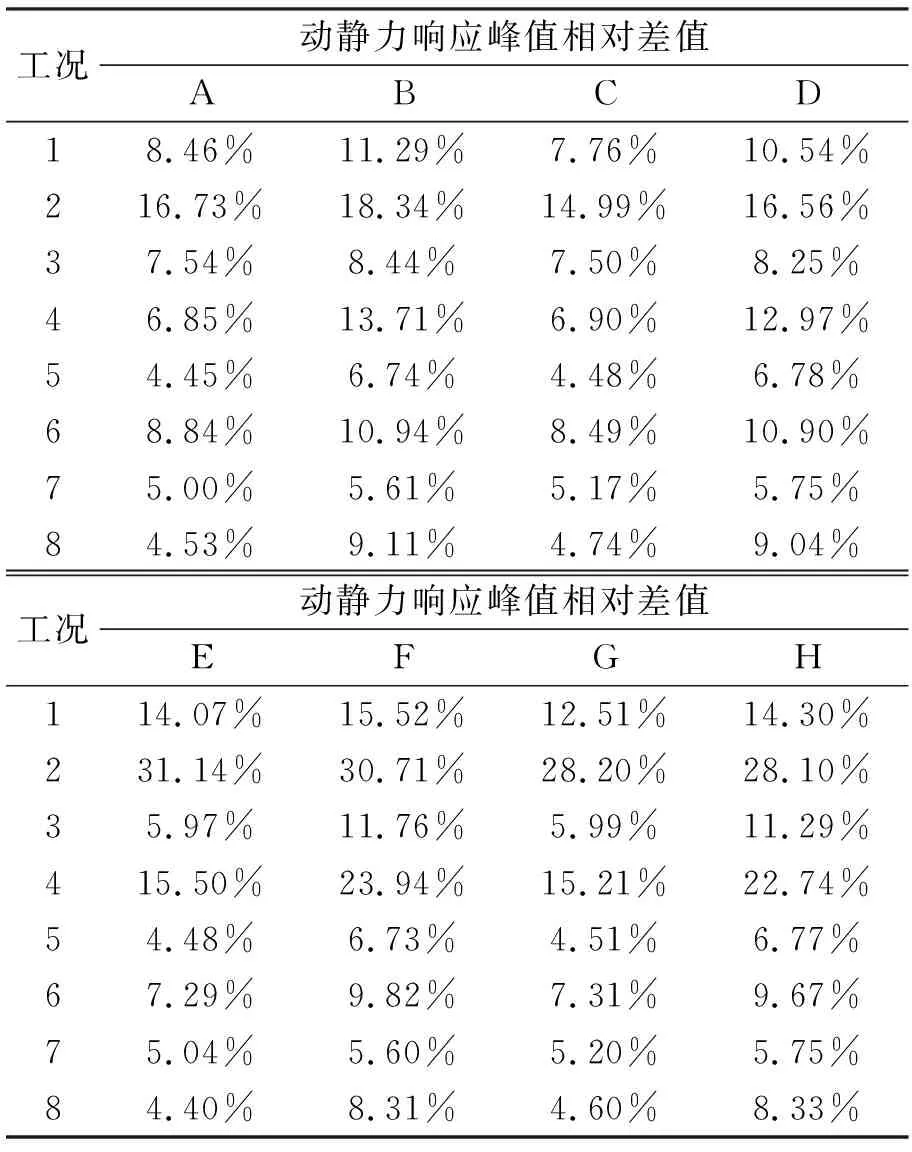
表4 各工况下典型部位杆件轴力动静力响应峰值对比
随着加载的进行,堆放在支撑架上的预制块不断增多,而小车动荷载却基本不变(小车动荷载只与正在运送的预制块的数量及分布情况相关,与已经运送就位的预制块数量无关)。相应地,小车动荷载所占总荷载(静+动)的比重降低。从整体上看,随着加载的进行,典型部位支撑架杆件动静力响应峰值之间的相对差值逐步降低。
在工况1~4中,堆放在支撑架上的预制块并不多,相对于最不利工况而言,支撑架杆件上的轴力要小很多。因此,尽管这些工况下动力响应放大系数很大,但并不会控制桥梁支撑架的设计,而真正控制设计的工况为加载即将完成的工况,如工况8。对于工况8来说,当小车运行速度为6 km/h时,计算得到的桥梁支撑架各典型杆件轴力动静力响应峰值相差约为4.28%~9.11%之间,均未超过10%,应该说此时小车动荷载对桥梁支撑架的影响并不是特别突出,在实际的桥梁支撑架设计分析中,可在静力分析的基础上,另外考虑一个10%左右的动力效应放大系数。
3 运送速度对支撑架的动力影响
前面给出了速度为6 km/h时各工况下动静力响应峰值的差值占静力峰值的比例。表5、6分别给出了速度增大到8 km/h和10 km/h时工况11和工况12下动静力响应峰值的差值占静力峰值的比例。

表5 工况11典型部位杆件轴力动静力响应峰值对比
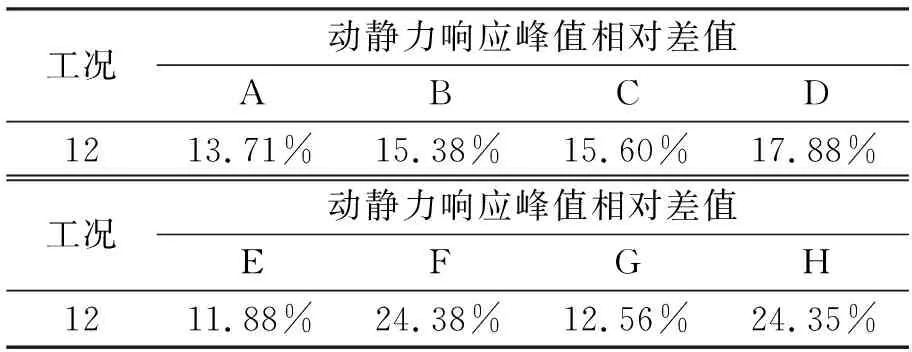
表6 工况12典型部位杆件轴力动静力响应峰值对比
根据前面的动静力响应峰值计算结果,典型支撑架杆件A、H的动静力响应峰值相对差值随速度的变化曲线如图8、9所示。从图中可以看出,随着速度的增加,各典型杆件的动静力响应峰值相对差值逐渐增大,即速度越大,动荷载对桥梁支撑架的受力影响随之增大,且从整体上看,速度越大,支撑架受力影响的增长速率越快。
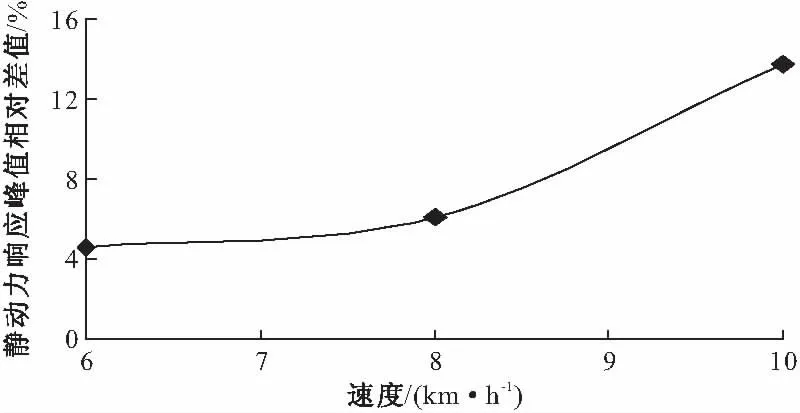
图8 A杆动静力响应峰值相对差值随小车速度变化曲线
4 结 论
(1)随着加载的进行,堆放在支撑架上的预制块不断增多,而小车动荷载却基本不变(小车动荷载只与正在运送的预制块的数量及分布情况相关,与已经运送就位的预制块数量无关)。相应地,小车动荷载所占总荷载(静+动)的比重降低。因此,随着加载的进行,典型部位支撑架杆件动静力响应峰值之间的相对差值逐步降低。
(2)小车运行速度越大,小车运送荷载在支撑架杆件中产生的轴力的波动越剧烈。从整体上看,随着小车运行速度的增长,动力响应峰值呈非线性增长,小车运行速度越大,动力响应峰值增长越快。
(3)小车动荷载主要对其正下方杆件的轴力影响较大,小车动荷载所到之处,其下方杆件轴力波动较为剧烈;随着小车的前行,杆件轴力波动剧烈的位置也随之前移。
(4)当小车运行速度为6 km/h时,计算得到的桥梁支撑架各典型杆件轴力动静力响应峰值相差约为4.28%~9.11%之间,均未超过10%,在实际的桥梁支撑架设计分析中,可在静力分析的基础上,另外考虑一个10%左右的动力效应放大系数。
[1] 徐崇宝, 张铁铮, 潘景龙,等. 双排扣件式支撑架工作性能的理论分析与试验研究[J]. 哈尔滨建筑工程学院学报, 1989, 22(2): 38-55.
[2] 黄宝魁, 徐崇宝, 张铁铮,等. 双排扣件式钢管支撑架整体稳定试验与理论分析[J]. 建筑技术, 1991, 18(9): 40-45.
[3] 黄 浩. 插销式支撑架半刚性节点机基本受力单元试验研究[D]. 重庆: 重庆大学, 2006.
[4] 魏銮新, 曾志兴. 扣件式钢管支撑架计算模型探讨与思考[J]. 福建建筑, 2010, 144(6): 113-116.
[5] 曾凡奎, 胡长明, 葛召深,等. 扣件式模板支架立杆的计算长度系数取值研究[J]. 工业建筑, 2010, 40(2): 24-27.
[6] 梁 波, 蔡 英. 不平顺条件下高速铁路路基的动力分析[J]. 铁道学报, 1999, 21(2): 84-88.
