竖向受荷桩的桩-土接触面简化模型

潘玉涛， 郑俊杰

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074 )

对于桩-土接触面的性质以及接触机理的问题，国内外学者已经做过一些研究。早期的接触面模型有无厚度的Goodman单元及Clough与Duncan等人[1,2]基于直剪试验的双曲线模型。但是这种无厚度的方法在使用时存在几个问题[3]：(1)在单元受压时，两侧的单元有可能相互嵌入；(2)求解法向位移有一个较小的偏差会引起法向应力的较大偏差。

Trochanis等[4]分析了桩土分离效应、桩周土体弹塑性性状等条件对桩-土接触面作用机制的影响。Desai等[5]提出了薄壁单元模拟接触面的理论，这可以避免两侧单元在受压时的相互嵌入，但是在使用时仍然存在一些局限：(1)薄壁单元剪切模量Gt=kst，与单元厚度有关，但是在使用时如何取t值来得到较准确的结果并未解决；(2)没有考虑法向变形和剪切变形的耦合作用。这两点都会带来较大的计算误差，不利于Desai的理论在工程实际中应用。Kucukarslan等[6]通过有限元与边界元的杂交耦合方法，将桩-土接触面用非线性耦合弹簧模拟，以获得一种兼顾精确性和实用性的方法。

FLAC3D手册[7]中提出了一种计算桩侧接触面侧向弹簧刚度的公式：

(1)

该公式考虑了直径对结果的影响，但是模拟效果并不好。

国内学者也对该问题做了一些理论与试验研究。张冬霁等[8]提出了剪切错动带的概念，在此基础上，通过试验与理论分析，给出了确定参数的方法。本文拟采用理论分析方法，考虑薄壁单元厚度、剪切刚度、屈服强度等参数对桩-土界面变形特性模拟的影响。通过参数分析，得出合理的剪切刚度和c、φ值取值范围。

1 薄壁单元剪切模量的取值

1.1 薄壁单元的刚度选取

如图1和图2所示，假设桩-土相互作用是通过周围一圈薄壁单元传递的，在竖向荷载不大的情况下，薄壁单元处于弹性阶段，弹簧刚度为ks；当竖向荷载较大时，薄壁单元发生屈服，考虑到薄壁单元的实质仍然是土体，屈服准则设定为常用于土体静力分析的摩尔-库伦屈服准则。

如图3所示，取一个微环隔离分析，竖向作用的应力只有环外土体的剪切应力、环内桩体的剪切应力、环面竖向的正应力以及体力。由平衡条件可得：

(2)

式中，A1为内环的面积，A1=2πrdz；A2为外环的面积，A2=2πRdz；A3为环上下面的面积，A3=π(R2-r2)；dz为微环的高度;σ为作用在环上的纵向正应力。当薄壁单元厚度较小时，前面两项为后面两项的高阶无穷小量，可以忽略不计。则式(2)只剩下：

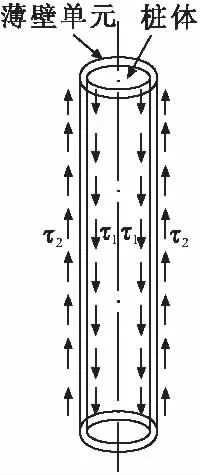
图1 桩-土接触面切向弹簧

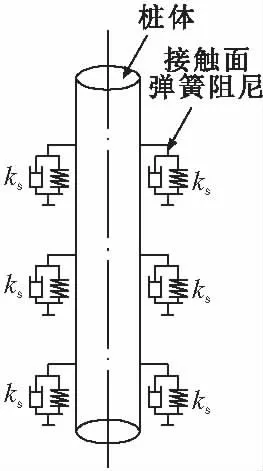
图2 桩侧薄壁单元

τ2A2-τ1A1=0

(3)

如图4所示，Δ为薄壁单元内外侧节点的沉降差值，t为薄壁单元厚度，桩侧摩阻力τ1与环内侧剪切应力大小相等方向相反，将其等效为刚度为ks的弹簧，有

τ1=KsΔ

(4)

剪切应力τ2与剪切变形有关，有

(5)

联立式(3)、(4)和(5)，得

(6)

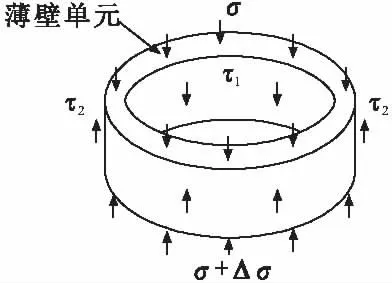
图3 薄壁单元受力

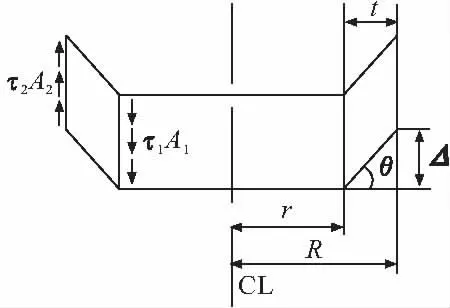
图4 薄壁单元变形几何关系

1.2 参数分析

本文运用FLAC3D建立单桩数值仿真模型如图5所示。模型尺寸为10 m×10 m×20 m，桩长10 m，桩径0.5 m，桩体弹性模量取为23 GPa，泊松比为0.3。桩周土体采用摩尔-库伦屈服准则，土体模量取50 MPa。桩侧薄壁单元采用摩尔-库伦屈服准则。为了比较各种薄壁单元方法在模拟土弹簧时的准确性，本文利用Desai薄层单元法、FLAC3D手册[7]中方法和本文方法分别模拟土弹簧侧向刚度为100 MPa时不同单元厚度的单桩竖向正压力2 MPa的情况，材料参数见表1。

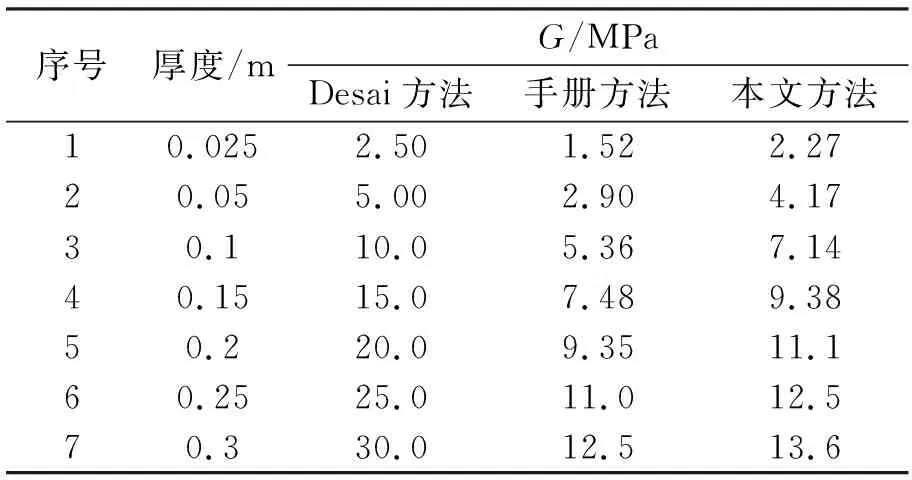
表1 桩径0.5 m时材料参数

如图6所示，在各种方法条件下，比较不同厚度薄壁单元模拟接触面时的桩顶沉降，可知手册中的方法模拟桩-土接触面效果较差，但是随着单元厚度的增大，模拟结果逐渐接近接触面弹簧得出的结果。Desai薄壁单元方法模拟结果在薄壁单元厚度比较小时结果较好，但是当薄壁单元厚度较大时，与接触面弹簧结果相差较大。所以如果薄壁单元厚度取值不当，会引起较大误差。

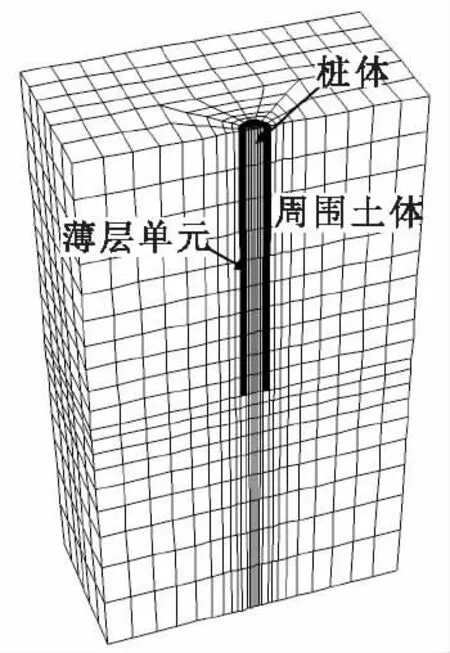
图5 计算模型

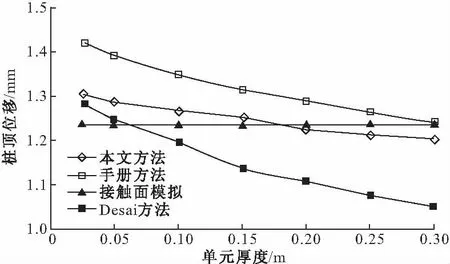
图6 D=0.5 m不同厚度薄壁单元的桩顶位移

限于篇幅，为了验证本文方法在不同桩径下的准确性，将桩径改为0.4 m(表2)。

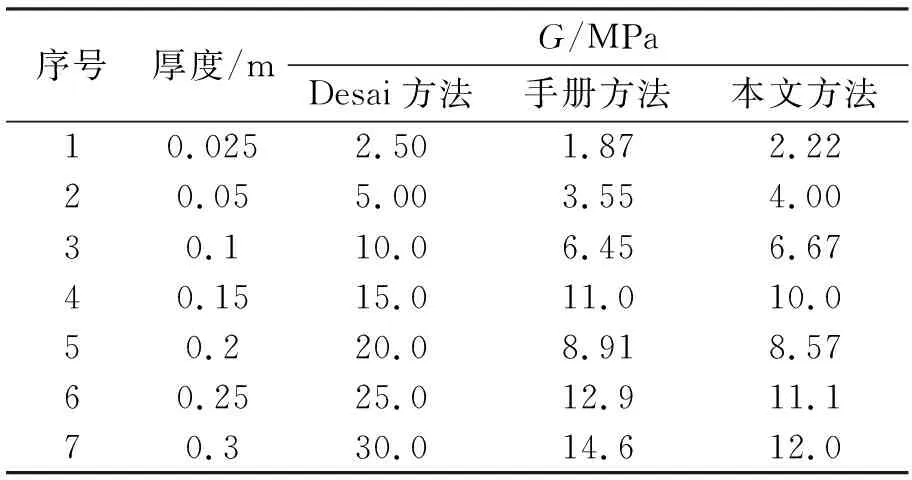
表2 桩径0.4 m时材料参数

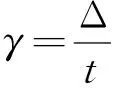
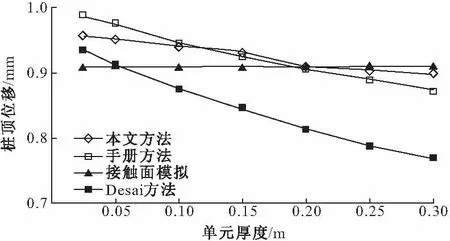
图7 D=0.4 m不同厚度薄壁单元的桩顶位移

采用本文方法计算得出的沿桩身轴向不同深度处桩身和薄壁单元外侧节点的竖向位移如图8所示，可以看出采用接触面弹簧模拟得出的桩身位移曲线处于0.1～0.3 m薄壁单元模拟得出的桩身位移曲线族之间，且两者大小变化规律非常相似。接触面外侧节点位移较薄壁单元外侧节点位移稍大，除在深度0～2 m范围内变化趋势不同外，在2～10 m范围内变化范围及大小相差不大。接触面弹簧模拟采用的是无厚度双节点模型，因此接触面外侧的竖向位移受到桩身竖向位移影响较大，于是产生的位移较大；而薄壁单元外侧节点距离桩身有一定距离，因此受到桩身竖向位移影响较小，故位移较小。且当竖向荷载较大时，薄壁单元发生剪切屈服，使单元内外侧节点竖向位移相差较大，即产生了一个剪切错动带。

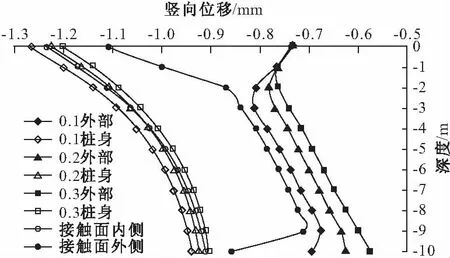
图8 本文方法与接触面模拟的沿桩长竖向位移的比较

2 薄壁单元强度参数的取值

2.1 薄壁单元强度的影响因素

前已述及，薄壁单元在弹性状态下能够通过剪切变形模拟接触面的刚度特性，当桩顶竖向荷载较大时，桩周土会发生屈服，及在桩周土应力不明显增加的情况下产生较大的变形。而在实际工程中，薄壁单元屈服强度的参数选取与以下几方面有关：

(1) 土体本身性质。薄壁单元所要模拟的桩周土体的性质与桩间土的性质相近，因此取值时应当参考场地土的性质。

(2) 成桩工艺。不同的成桩工艺对土体的扰动不同，对土体扰动较大的成桩工艺导致桩周土强度较低，应该取较低的c、φ值。对桩间土的挤密效果较好的成桩工艺导致桩间土的强度提高，应该取较高c、φ的值。

图9 摩擦角和内聚力对桩顶位移的影响

2.2 分 析

如图9所示，随着摩擦角增大，桩顶位移逐渐减小，当摩擦角增大到一定程度时，桩顶位移变化不明显。桩顶沉降在一定范围内随着内聚力线性减少。由摩尔-库伦屈服准则可知，随着摩擦角的增大，单元的屈服强度增大。荷载不变，摩擦角越大，薄壁单元进入塑性状态越慢，从而桩顶位移越小。同理，在荷载不变时，随着内聚力增大，单元屈服强度也增大，桩顶位移减小。

此外，随着摩擦角的增大，薄壁单元与薄壁单元外侧桩周土体逐渐进入塑性状态。塑性区的发展趋势表现为自上而下，从靠近桩边缘到远离桩体。

3 结 论

(1) 本文方法在厚度0.025～0.3m范围内计算结果稳定性较好，计算精度不会随着薄壁单元厚度和桩径的改变而产生较大变化。薄壁单元模拟的竖向位移分布规律与接触面弹簧模拟非常相似，薄壁单元厚度限定在一定范围内时，可以用薄壁单元替代接触面弹簧从而减少因为耦合弹簧产生的计算代价。

(2) 随着摩擦角增大，桩顶位移逐渐减小，当摩擦角增大到一定程度时，桩顶位移变化不明显。桩顶沉降在一定范围内随着内聚力线性减少。

本文通过理论推导得到薄层单元模拟接触面的单元厚度和单元刚度参数的选取方法，并对强度参数对接触面变形性状进行了分析。在一定程度上减少了因使用耦合弹簧所增加的计算代价。但是，不同的桩-土相互作用类型和荷载情况下，桩-土接触面的强度问题不是一成不变的。要探索这个问题，必须对各种类型的接触面进行大量的试验来进行研究。

[1] Goodman R E, Taylor R L, Brekke T L. A model for the mechanics of jointed rock[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(3): 637-659.

[2] Clough G W, Duncan J M. Finite element analysis of retaining wall behavior[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 99(4): 347-349.

[3] 李素华, 殷建华，周建,等. 端承型基桩的桩-土作用机理研究探讨[J].岩石力学与工程学报，2004, 23(6): 996-1000.

[4] Trochanis A M, Bielak J, Christiano P. Three- dimensional nonlinear study of piles[J]. Journal of Geotechnical Engineering, 1991, 117(3): 429-447.

[5] Desai C S, Nagaraj B K. Modeling for cyclic normal and shear behavior of interfaces[J]. Journal of Engineering Mechanics, 1988, 114(7): 1198-1217.

[6] Kucukarslan S, Banerjee P K. Inelastic analysis of pile- soil interaction[J]. Journal of Geotechnical and Geo-environmental Engineering, 2004, 130(11): 1152-1157.

[7] ITASCA Consulting Group. Fast Lagrangian Analysis of Continuain 3 Dimensions Users Manual[Z]. USA: Itasca Consulting Group, 1997.

[8] 张冬霁,卢廷浩. 一种土与结构接触面模型的建立及其应用[J]. 岩土工程学报, 1988, 20(6): 62-66.