粗粒土三轴试验的细观模拟

耿 丽， 黄志强， 苗 雨

(1.华中科技大学 土木工程与力学学院， 湖北 武汉 430074；2.中国地质大学(武汉) 工程学院， 湖北 武汉 430074)

粗粒土泛指冲洪积砂卵石、采挖堆石、冰碛土、砾质土以及各种软岩风化料[1]。粗粒土储量丰富，广泛应用于土石坝、道路、护岸抛石体、河堤、江堤、海湾防波堤等工程。长期以来，人们借助传统的室内试验来研究粗粒土的强度及变形特性，得到一些有意义的结论。秦红玉[2]等通过三轴试验研究了粗粒料中不同泥岩含量对堆石坝料强度的影响；姜景山[3]通过大型三轴压缩试验研究了密度、围压对粗粒土力学性质的影响，并分析了围压对应力应变曲线的影响；刘萌成[4]利用三轴试验研究了不同应力路径条件下堆石料的剪切特性；Bagherzadeh-Khalkhali[5]研究了粗粒土最大粒径对抗剪强度的影响。

尽管三轴试验应力状态简单，但由于边界条件、径径比(试验仪器直径与试样颗粒最大直径之比)、颗粒强度等因素也给试验结果带来很多不确定性[6]。众所周知，试验成果具有价值的前提就是具有规律性，直接或间接反映材料的某个物理力学特性，但室内三轴试验数据往往具有很大离散型。数值试验可以根据试验目的灵活地选择试验条件及控制因素，准确快捷地得到较完备的试验数据，使试验和数据处理更为灵活，突破了常规试验仪器设备能力、试验条件上的局限性。目前，用数值方法模拟粗粒土三轴试验的研究虽然还不多，但也取得了一些成果。周健等[7]对砂土在不排水循环荷载作用下的液化特性进行了颗粒流数值模拟，探讨了液化的细观力学机制。王学滨等[8]利用快速拉格朗日分析法模拟了尺寸效应、加载速率和围压等因素对假三轴试件抗压应力-应变全过程曲线的影响，分析了变形局部化启动、稳定、剪切带图案及其演化规律。邵磊等[9]按照堆石料试件级配和密度生成PFC3D数值模型模拟了堆石料的三轴试验。王光进等[10]开发了不同颗粒初始架构粗粒土试样的HHC-CA模型，借助FLAC3D分析了砾石含量对摩擦角的影响；杨贵等[11]采用三维颗粒流程序研究了不同平均主应力和中主应力系数下粗粒料的变形和强度特性。

粗粒土细观结构的复杂性和不确定性是对其力学行为进行准确描述的最大障碍，组成粗粒土的颗粒之间的相互作用及排列方式都影响着粗粒土的强度及变形，因此本文从细观角度出发，以PFC3D为工具，根据粗粒料的级配曲线自编程得到数值模型，从细观角度分析了颗粒摩擦系数，颗粒间黏结力，并着重分析了颗粒形状等因素对粗粒土强度的影响。

1 三维颗粒流基本理论

1.1 PFC基本原理

颗粒流法是基于离散元思想来模拟刚性圆球运动及相互作用的一种简化离散元方法。计算原理是利用中心差分法进行动态松弛，计算过程是在每个时步内交替运用牛顿第二定律和力-位移定律，时步迭代并遍历整个颗粒集合体。牛顿第二定律根据颗粒间接触力及颗粒体力确定颗粒运动，更新颗粒的运动速度及颗粒与颗粒(或墙)的位置；力-位移定律通过每个接触点的相对运动及接触模型来更新每个接触力。

根据力-位移定律，得到接触面上的接触力。接触力在接触面上分为法向量和切向量。其中法向接触力为Fn=KnUnni，式中Kn为法向刚度；Un为法向位移，即颗粒与颗粒之间或颗粒与墙之间的重叠量；ni为接触面法向单位向量。

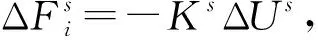
1.2 PFC黏结接触模型单元

BPM(bonded-particle model)表示通过内聚力、摩擦黏结力、接触及黏结处的有限刚度将不同大小的圆球颗粒黏结在一起的颗粒集合体。本文所用BPM程序是ITASCA公司于1995年开发的，是PFC的传统模型。此处的“颗粒”是指占据有限空间的刚性圆球，它们只在软接触处相互作用并可以相互“重叠”。此接触处的细观性质被两种黏结模型支持：接触黏结模型(contact-bond model)和平行黏结模型(parallel-bond model)。这类引入黏结(bond)的颗粒模型为BPM(bonded-particle model)模型。此类系统的运动由牛顿第二定律描述。BPM模型要满足以下假设：(1)颗粒是数量有限的刚性圆球；(2)颗粒之间相互独立，颗粒可以平动和转动；(3)颗粒只在接触处相互作用；(4)颗粒之间允许重叠，但重叠量远小于颗粒尺寸；(5)颗粒间黏结可以承受一定荷载或破裂；(6)黏结接触处满足力-位移定律。

由于PFC3D基本单元为刚性圆球，而组成粗粒土的单元颗粒形状不规则，颗粒之间不仅存在摩擦力，由于相互嵌固还存在咬合作用，因此为了近似增大颗粒间接触力，本文引入黏结接触的BPM模型。接触黏结力包括法向黏结力和切向黏结力，切向黏结增大了颗粒间的摩擦，法向黏结力则使颗粒之间承受压力和拉力。

1.3 细观参数与宏观力学行为之间的关系

PFC输入的属性参数不能由试验结果直接确定，因为得到集合体过程中的颗粒大小及组装方式等因素影响着数值模型的力学行为。在固定颗粒大小及组装方式的前提下，PFC模型参数和可以选择的颗粒材料参数之间必须通过相应的数值模拟试验(如三轴试验、巴西劈裂试验等)来建立彼此之间的关系和联系，这是个不断尝试的过程，通常称为标定。标定常以PFC模型的应力应变关系及破坏包线与试验结果相符为标准，并且此标定过程与应力路径无关。

材料的弹性模量主要受颗粒细观模量影响，在一定范围内，弹性模量随细观模量的增大而增大；法向刚度与切向刚度的比值影响泊松比；颗粒间的摩擦又对材料的峰值强度有一定影响。PFC中细观参数对材料宏观力学性质的影响不是独立的，而是相互影响共同作用的。

PFC模型参数的输入，是一个极为费时的过程，目前也只有定性的参考，在文献[12]、[13]中均有涉及，文献[14]对脆性岩石的标定进行了定量的统计，提供了一定的指导和参考。

2 粗粒土室内三轴试验

2.1 试验材料及制备

三轴试验的粗粒土取自某排土场，由于粗粒土粒径及试样尺寸的限制，需对原材料进行原始级配尺寸缩尺。根据试样直径与颗粒最大粒径比等于5时，试验结果对抗剪强度影响最小，取样品最大粒径为60 mm，先按照相似法将原样粒径等比例缩小3倍，再等量代替，保持粒径小于5 mm的细料含量不变。试验所用材料母岩为千枚岩，试样干密度为1.88 g/cm3，粗料含量(颗粒粒径大于5 mm的质量百分比)为78%。

2.2 试验仪器与方法

图1 三轴仪

三轴试验仪器采用YLSZ30-3型应力式大型三轴剪切仪，如图1，压力室高600 mm，直径300 mm。根据试验要求的干密度、试验尺寸和级配曲线(图2)计算并称取试验所需的粗粒土试验样品，混合均匀，分3层装料振实，得到粗粒土试样如图3。采用各向等压固结排水(CD)剪切的试验方法，抽气联合水头饱和，试验采用应变控制，以轴向应变速率0.03 mm/min进行剪切，至轴向应变达到15%时终止试验。为研究堆体的强度和变形特性，在饱和状态下分别进行围压为0.4 MPa、0.8 MPa、1.6 MPa下的常规大型三轴排水固结试验。

图2 粗粒土试验级配曲线

图3 粗粒土三轴试验

3 粗粒土三轴试验数值模拟

3.1 数值试样的生成

粗粒土三轴数值模型试件为高60 cm，直径为30 cm的圆柱体，上下平面为加载板，其刚度略大于颗粒法向刚度；壁柱为柔性约束，法向刚度小于颗粒的法向刚度。由PFC3D内嵌fish语言根据室内试验的颗粒级配曲线编写程序，得到与室内试验材料级配一样的颗粒集合体。在得到颗粒集合体过程中如果完全按实际情况取粗粒土最小粒径为0.1 mm，则生成颗粒数目可达65万之多，极为费时，所以在此数值模型生成颗粒集合体时，最小粒径控制在1 mm，所用粒径组及其百分比见表1，得到的PFC3D颗粒集合体如图4。

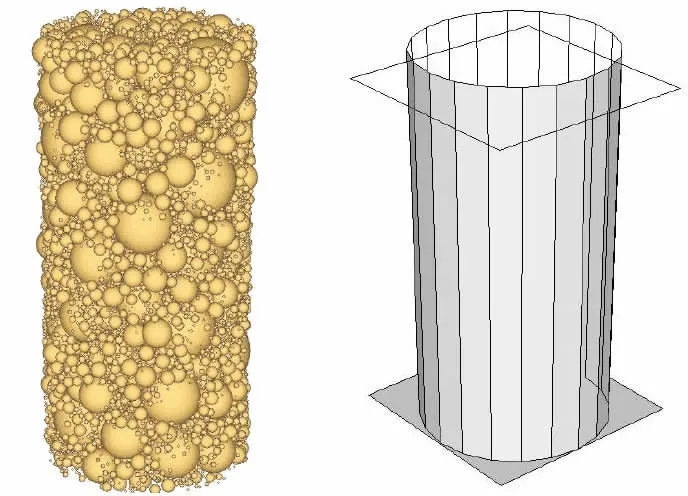
图4 PFC3D数值模型

粒径组/mm60-4040-2020-1010-55-1质量百分数/%16.624.3720.8516.1822

3.2 细观参数的标定

(1)标定颗粒弹性模量Ec和法向强度与切向刚度比值kn/ks。引入接触黏结模型的数值模型宏观弹性模量主要由颗粒弹性模量Ec和刚度比kn/ks决定。在颗粒大小分布及kn/ks的值一定时，细观模量Ec和宏观模量E线性相关，E随着Ec的增大而增大。执行PFC3D三轴试验，不断调整Ec的大小直至模型的弹性模量与试验值一致，此时的细观模量即为要输入的细观参数。刚度比kn/ks主要通过与泊松比的匹配确定，泊松比随着刚度比的增大而增大。确定Ec、kn/ks后，由PFC3D中kn=4REc确定kn值，再由kn/ks的值确定ks的大小。

(2)标定颗粒间黏结强度σc、τc。颗粒间黏结强度σc、τc主要与材料的峰值强度相关。不同的围压下，当黏结强度标准差与均值的比值(σs/σm)及切向黏结强度与法向黏结强度的比值τc/σc一定时，材料的峰值强度与黏结强度均值成正比。强度比值τc/σc影响着材料的破坏形式，当比值较小时材料发生脆性破坏，比值较大时材料发生塑性破坏，一般比值取1。确定了材料的弹性参数后，执行一系列三轴试验当数值模型的峰值强度与试验值相符时所确定的法向黏结强度均值即为细观参数输入值，再根据强度比值τc/σc确定切向黏结强度。

(3)摩擦系数的确定。摩擦系数对材料的弹性性质影响不大，只与峰值强度有关，目前还没有统一的标准来定性定量地确定其输入值的大小。

本文根据室内三轴试验得到的峰值强度、弹性模量、泊松比等宏观参数，结合细观参数与宏观响应之间的关系，通过标定过程的反复尝试和调整，得到了一组较为理想的PFC3D细观参数，其值见表2。

表2 颗粒流数值模拟细观参数

3.3 PFC3D数值试验的实现

PFC3D由伺服控制系统通过上下加载板作相对运动进行等压固结，加载板移动速度控制为0.2 mm/s。由于PFC的计算原理是以牛顿第二定律控制的动态模式为基础，时步(Δt)在计算循环中应无限小，0.2 mm/s虽然在实际中比较大，但在PFC中，相当于移动1 mm需要以6.7-6mm/s的速度移动105时步，这充分保证了试样在每个时步内都保持准静态平衡。通过fish函数自动调整壁柱位移来保持围压不变，并严格控制围压的误差在加载过程中小于1%，使试样在每一步的平衡状态下加载，直至轴向应变达到15%，加载过程停止。对于BPM及CLUMP颗粒模型分别在围压为0.4 MPa、0.8 MPa、1.6 MPa工况下进行加载。

4 数值模拟结果分析

4.1 数值结果与室内试验结果对比

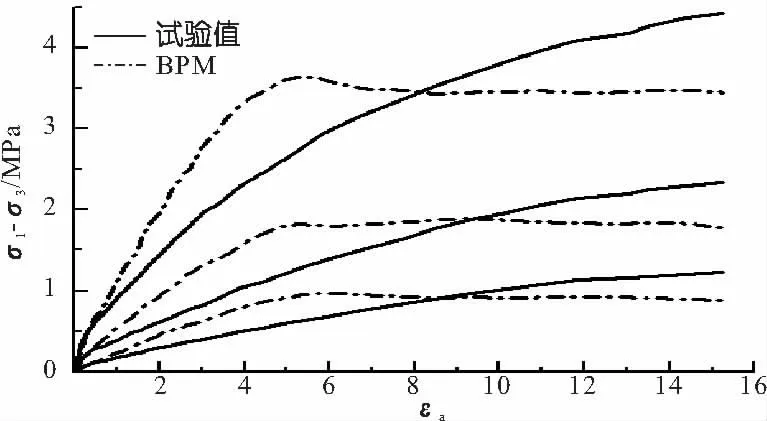
图5 PFC模型与试验应力应变曲线

如图5所示，数值模拟结果与试验结果总体趋一致，但偏应力值略有偏差，并且随着围压的增加，这种偏差越来越大。这与Potyondy和Cundall[8]的分析是一致的，传统PFC模型下的三轴数值试验应力-应变曲线只在低围压下与试验值吻合。主要原因在于PFC的基本单元为刚性圆球，颗粒形状及排列形式单一、颗粒之间相互嵌固及咬合作用力弱，虽然引进了接触黏结来提高颗粒间接触力，但随着轴向荷载的增大，黏结破裂，其对抗剪强度的贡献极为有限，与实际粗粒土强度特性相差较大。

4.2 接触摩擦对强度的影响

如图6所示，当其他细观参数一定时，曲线峰值强度随着颗粒间摩擦系数的增大而提高，材料的初始弹性模量也略有增大，但残余强度差别不大。当BPM颗粒由于转动或剪切力过大造成黏结破坏时，作用于颗粒接触处的残余力主要取决于法向压力及颗粒间的摩擦系数。接触处的摩擦力能够抑制颗粒间的转动或滑移，摩擦系数越大，颗粒间相互作用也越大，这个过程能够增加粗粒土的抗剪强度。

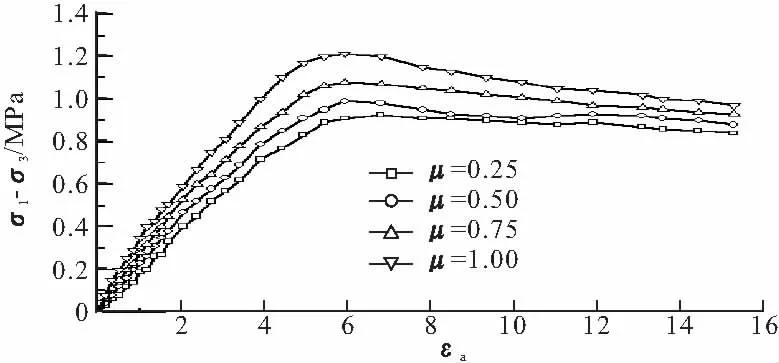
图6 400 MPa时不同摩擦系数下应力应变曲线

4.3 黏结强度对强度的影响

粗粒土受剪切的破坏面并非平面，其抗剪强度来源也并不是只有颗粒表面的内摩擦力。剪切面上的粗颗粒阻挡剪切形成不规则的曲面，这种粗粒土颗粒相互交错镶嵌的排列而产生抗剪切的阻力为咬合力[15]，其使粗粒土的强度大幅度提高。粗粒土的咬合力主要来自不规则颗粒间嵌固咬合作用，而PFC模型中基本单元为圆球，与实际颗粒特性相差甚远，为了模拟颗粒间咬合力，引入接触黏结模型，法向黏结力模拟颗粒间拉、压作用，切向黏结力不仅增大了颗粒间摩擦，也对咬合力有所贡献。在加载过程中，随着轴向压力的增大，颗粒间接触力增大，当接触力未达到黏结强度时，主要由颗粒间黏结力抵抗荷载剪切作用。由图7可知，峰值强度之前随着黏结强度的增大，偏应力提高，当轴向荷载施加的作用使得颗粒间接触力超过黏结强度或由于颗粒的转动导致黏结破坏时，抗剪强度只有摩擦力承担，所以不同黏结强度的残余应力基本相同。

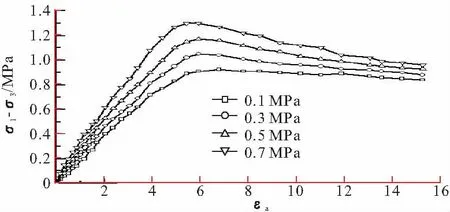
图7 400MPa时不同黏结强度下应力应变曲线

4.4 颗粒形状对强度的影响

由以上结果分析可以看出，以黏结的圆球为单元的传统PFC模型在不同围压下的抗剪强度一直低于试验值，由Potyondy、cundall[12]及N.Cho[13]及Hoek[16]等的分析可以知道这是传统PFC模型无法克服的缺陷。而改变颗粒的细观力学参数，如提高摩擦力及黏结强度，对克服这些缺陷收效甚微。池永和周健[17]用颗粒离散元模拟砂土的双轴试验，通过改变颗粒性质及颗粒大小和分布得到与试验相符的模拟结果，但数值模型中将砂土颗粒简化为圆形颗粒，其颗粒间咬合远小于实际情况，在模拟时，他们人为地把颗粒摩擦系数取很大值，最高达80，这显然不合逻辑，也不能真正反映摩擦力和咬合力对砂土强度的贡献。

从以上讨论可知，影响粗粒土强度的最主要因素不是细观接触参数而是颗粒几何条件。由N.Cho[13]分析可知，依据实际颗粒形状引入不同几何特性的CLUMP颗粒，就可以明显提高PFC模型的抗剪强度。

在PFC3D中CLUMP是由多个圆球胶结在一起，用以模拟非规则形状颗粒或块体的超级颗粒。无论多大荷载作用于CLUMP颗粒上，其都不会破裂，这点区别于引入黏结模型的BPM模型。并且组成CLUMP颗粒的内部圆球之间的接触力不参与循环计算，这大大提高了计算效率。由于生成CLUMP颗粒，非常费时，本文仅用2个、3个圆球得到两种CLUMP颗粒单元，并随机生成，用以模拟粗粒土中不同形状的颗粒。得到的CLUMP颗粒体积及重量与原球形颗粒相同，只改变了颗粒形状。由CLUMP颗粒得到的集合体，其应力应变曲线如图8。

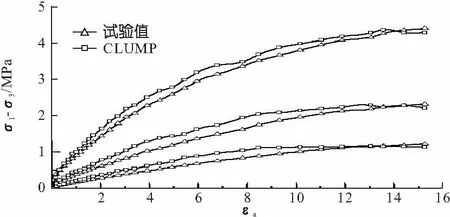
图8 CLUMP数值模型与试验应力应变曲线

由图可知，随着围压的增大，CLUMP颗粒模型的偏应力值也在提高，在不同围压下CLUMP颗粒得到的数值模型的应力应变关系曲线与试验结果吻合很好，因为CLUMP颗粒近似模拟了实际粗粒土中颗粒的不规则性，增大了颗粒间的嵌固，提高了咬合作用，并且在加载过程中，要克服颗粒之间错动需要很大能量，所以CLUMP颗粒模型显著地提高了PFC模型的抗剪强度。

5 结 论

粗粒土是不同粒径的颗粒集合体，本文在室内固结排水三轴试验的基础上，从细观角度出发，以PFC3D为工具，根据室内试验材料的级配和密度得到粗粒土三轴试验数值模型。通过改变数值模型中粗粒土颗粒之间的摩擦及黏结强度、颗粒形状等因素，分析影响粗粒土强度的细观因素，得出了以下结论：

(1) 用三维颗粒流数值模型模拟粗粒土室内三轴试验，可以灵活改变试验条件，快捷准确的得到不同工况下的试验数据，克服了室内三轴试验设备能力的局限性及试验结果的离散型。

(2) 引入接触黏结本构的PFC3D三轴试验模型得到的应力应变曲线与试验结果趋势一致，但不同围压下的偏应力值都低于试验结果。

(3) 在BPM模型中提高摩擦系数，黏结强度等力学性质可以提高PFC三轴模型的偏应力值，但改变量很小。

(4) 在PFC模型中引入CLUMP颗粒改变颗粒形状可以有效的提高抗剪强度，得到的应力应变曲线与试验值吻合较好。

[1] 司洪洋. 论无粘性砂卵石与堆石的力学性质[J]. 岩土工程学报, 1990, 12(6): 32-41.

[2] 秦红玉,刘汉龙,高玉峰,等.粗粒料强度和变形的大型三轴试验研究[J].岩土力学,2004, 25(10):1575-1580.

[3] 姜景山,刘汉龙,程展林. 密度和围压对粗粒土力学性质的影响[J].长江科学院院报,2009,26(8): 46-50.

[4] 刘萌成, 高玉峰, 刘汉龙. 应力路径条件下堆石料剪切特性大型三轴试验研究[J]. 岩石力学与工程学报,2008,27(1):176-186.

[5] Ahad Bagherzadeh-khalkhalia, Mirghasemi A A. Numerical and experimental direct shear tests for coarse-grained soils [J]. Particuology, 2009, 7(1):83-91.

[6] 程展林,丁红顺. 论堆石料力学试验中的不确定性[J]. 岩土工程学报, 2005, 27(10):1222-1225.

[7] 周 健,杨永香,刘 洋,等. 循环荷载下砂土液化特性颗粒流数值模拟[J]. 岩土力学, 2009, 30(4): 1083- 1088.

[8] 王学滨, 潘一山, 盛 谦, 等. 岩体假三轴压缩机及变形局部化剪切带数值模拟[J]. 岩土力学, 2001,22(3): 323-326.

[9] 邵 磊,迟世春,贾宇峰. 堆石料大三轴试验的细观模拟[J].岩土力学,2009, 30(s1)：239-243.

[10]王光进, 杨春和, 张 超, 等. 粗粒土三轴试验数值模拟与试样颗粒初始架构初探[J]. 岩土力学, 2011, 32(2):585-592.

[11]杨 贵,肖 杨,高德清. 粗粒料三维颗粒流数值模拟及其破坏准则研究[J].岩土力学, 2010,31(s1): 402-406.

[12]Potyondy D O, Cundall P A. A bonded-particle model for rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2004,41(8):1329-1364.

[13]Cho N, Martin C D, Sego D C. A clumped particle model for rock [J]. International Journal of Rock Mechanics and Mining Sciences, 2007,44(7):997-1010.

[14]Jeoungseok Yoon. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 871-889.

[15]陈希哲. 粗粒土的强度与咬合力的试验研究[J]. 工程力学, 1994,11(4):56-63.

[16]Hoek E, Brown E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 34(8):1165-1186.

[17]周 健, 池毓蔚, 池 永,等. 砂土双轴试验的颗粒流模拟[J]. 岩土工程学报, 2000,22(6):701-704.