高速铁路路基粗粒土填料颗粒破碎演化特征研究
2021-06-24王启云肖南雄张丙强项玉龙魏心星
王启云 ,肖南雄,张丙强 ,项玉龙,魏心星
(1.福建工程学院 土木工程学院,福建 福州 350118;2.福建工程学院 地下工程福建省高校重点实验室,福建 福州 350118)
由于粗粒土具有良好的工程特性,因而被广泛用作高速铁路路基基床填料[1]。路基作为高速铁路的主要承重结构,承受轨道与路基的自重及列车荷载,其强度、刚度及变形特性影响轨道的平顺性和列车运营的安全性。在填筑压实荷载及高速列车动荷载作用下,粗粒土路基中粗颗粒破碎形成较小粒径的颗粒,导致土体颗粒级配发生改变,颗粒重新排列、分布,进而影响粗粒土的工程特性。因此,研究高速铁路路基粗粒土填料在压实荷载和动力荷载受力全过程的颗粒破碎特性,对工程实践具有重要的指导意义。目前,针对粗粒土的颗粒破碎特性,国内外学者采用直剪试验[2]、数值模拟[3]、大型三轴试验[4,6]、大型击实试验[7]等方法,考虑不同的颗粒级配、不同的影响因素开展了大量的试验研究工作。INDRARATNA等[4−5]通过三轴试验发现动力循环加载次数以及加载频率的提高将导致粗粒料颗粒破碎程度的提高。蔡正银等[6]通过剪切试验研究了级配、密度、围压对堆石料的颗粒破碎规律,建立分形维数与级配、围压的关系式。杜俊等[7]利用击实试验指出粗粒含量与含水率对颗粒破碎具有重要影响。张振东等[8]利用动力加载试验研究围压、固结比及动应力幅值的颗粒破碎特性。对于颗粒破碎量化指标,MARSAL 等[9−13]分别采用Bg,Br,B*r,Br50和Dm来度量颗粒破碎大小。国内外学者针对粗粒土颗粒破碎的研究取得了系列成果,在研究中考虑了动应力、加载次数、应力比、含水率等因素的影响。但现有成果还未深入考察加载频率、降雨入渗强度对颗粒破碎的影响,尤其是不能反映高速铁路路基粗粒土填料的破碎动态演化过程。为此,本文构建粗粒土填料单元模型,分别采用压实试验、动力循环加载试验模拟粗粒土填料在填筑过程和高速列车运行过程中的受力状态,重点考虑动应力幅值(列车荷载)、加载频率(列车速度)及降雨入渗强度等因素的影响,分析粗粒土填料的颗粒破碎特性,为高速铁路路基填料选择与变形控制提供参考。
1 试验方案
1.1 试验材料与模型箱
为获得符合《铁路路基设计规范》要求的粗粒土填料,将黏性土与碎石进行拌合,碎石为弱风化粉砂岩,棱角分明,粒径范围2~40 mm,试样级配累计曲线见图1。采用大型粗粒土重型击实仪测得土样最大干密度为2.17 g/cm3,最优含水率为6%,饱和含水率为14.1%。
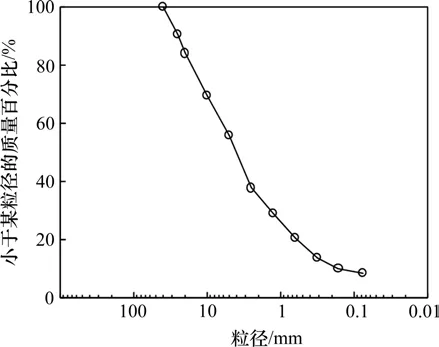
图1 试样颗粒级配曲线Fig.1 Particle size distributions of tested materials
试样采用方柱体,边长为20 cm,高度为40 cm,最大颗粒为4 cm,填筑在模型箱内。考虑《铁路路基设计规范》对高速铁路粗粒土填料的压实度要求,本次试验试样的压实系数均取0.95。为模拟路基土体的受力状态,模型箱的两侧采用L型钢板约束该方向的变形,另外两侧采用弹簧和钢板模拟相邻土体对粗粒土填料的约束。模型箱如图2所示。
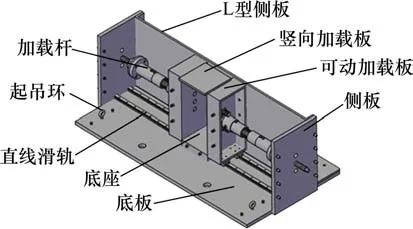
图2 模型箱三维图Fig.2 3D model box
1.2 压实试验方案
为模拟粗粒土填料填筑过程,采用千斤顶分3层将土样填筑在模型箱内,每层高度约13.3 cm,以保证试样的压实度及均匀性。压实过程示意如图3。压实度达到0.95 后,停止加载。试验结束后,先洗筛去除黏土颗粒,放置室内自然风干、烘干,再对每个试样的颗粒进行筛分,获得压实后试样颗粒级配。为避免试验误差,共制备3个压实试样。
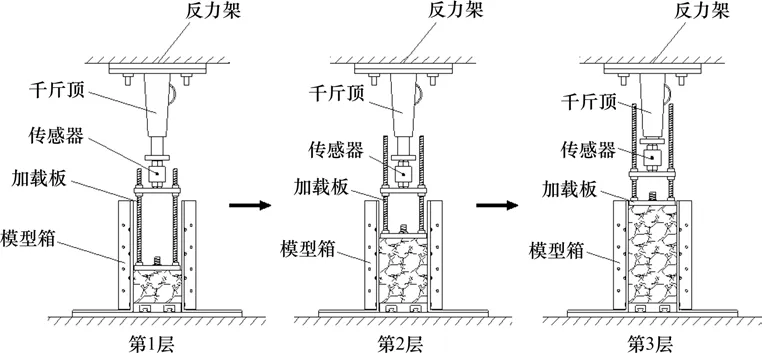
图3 压实示意图Fig.3 Compaction diagram
1.3 动力循环试验方案
为模拟高速列车对粗粒土填料的动力荷载作用,采用高速高性能液压伺服加载系统(MTS系统)对压实后的试样施加动力循环荷载,如图4所示。

图4 动力循环试验系统Fig.4 Dynamic loading cycle system of test
现有研究[14−15]表明,时速小于350 km/h 的高速铁路路基表面动应力实测值一般不超过110.5 kPa,路基基床底层和路基本体填料动荷载作用主频率在2~12 Hz 之间。因此,考虑动应力幅值、加载频率及降雨入渗强度等因素的影响,共制备24 组试样,具体分组如表1 所示,其中试样A(1-16)主要考虑动应力幅值σdmax(25,50,100 和200 kPa),加载频率f(2,4,6 和8 Hz)的影响,试样B(1-8)主要考虑降雨入渗强度w的影响,试样C(1-3)主要考虑加载次数N的影响。
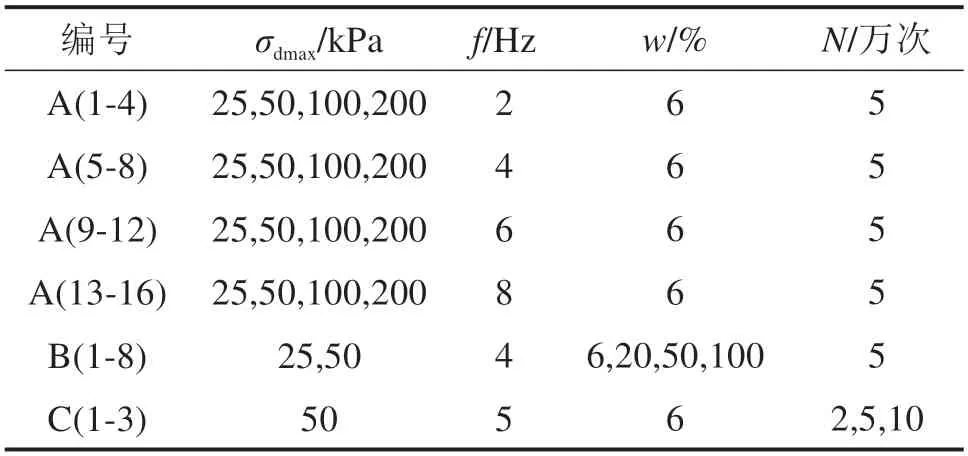
表1 试验分组情况Table 1 Test group
动力加载前,先对试样施加25 kPa 竖向压力,模拟基床底层表面的应力环境。循环荷载采用正弦波,波形如图5所示。
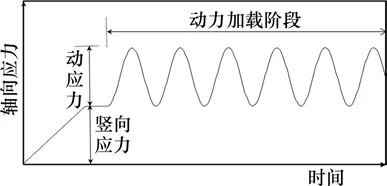
图5 动力加载波形Fig.5 Dynamic loading waveform
为模拟降雨入渗强度对颗粒破碎的影响,在B组试样填筑后,3 h 内从试样表面分别浇入水4.9,16.1 和32.8 kg,使渗入试样总水量达到试样土颗粒质量的20%,50%和100%。同时模拟雨水排出过程,允许多余的雨水从试样中自由渗出。动力循环加载试验结束后,对整个试样进行筛分,获得试样颗粒级配。
2 试验成果分析
2.1 压实试验后试样颗粒破碎特征
利用压实试验前后试样的颗粒级配曲线,计算获得了各粒组的颗粒含量变化如图6所示。
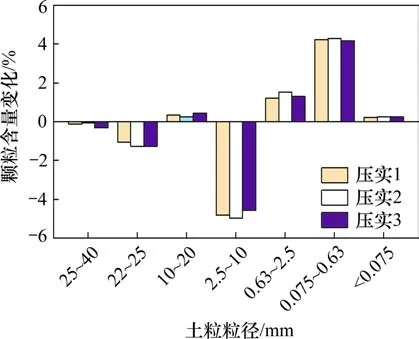
图6 压实后颗粒含量变化Fig.6 Changes in particle content after compaction
由图6可以看出,经过压实后,粗粒土填料出现明显的颗粒破碎。在压实过程中,粗粒土填料中粒径在20~40 mm,2.5~10 mm 的颗粒含量分别减少约1.2%,4.3%,粒径在2.5 mm 以下的颗粒含量明显增大,且主要集中在0.075~2.5 mm,增加约为4.2%,粒径在0.075 mm 以下的颗粒含量增加较小,增加约0.5%。分析表明,在压实过程中,粗粒土填料的颗粒破碎方式以破裂、破碎为主,研磨为辅。
从图6中还可以看出,在相同压实条件下,试样的粒径含量变化规律基本一致,且数值接近,说明压实过程具有代表性,可采用分层压实的方法制备动力循环试验的试样,将3组压实试样级配的均值作为动力循环加载试验的基准级配。
2.2 动力循环加载后试样颗粒破碎特征
利用动力循环加载后试样的颗粒级配和压实制样后试样的基准级配,计算获得了不同加载频率条件下颗粒含量变化,如图7和图8所示。
从图7 和图8 可以看出,在动力循环荷载作用下,粗粒土填料出现明显的颗粒破碎。各试样中粒径为25~40 mm,10~20 mm和0.63~2.5 mm的粒组颗粒含量明显减少,而粒径为20~25 mm,2.5~10 mm,小于0.075 mm 的粒组颗粒含量明显增大,各试样增加或减小的粒组较为一致,说明颗粒级配对颗粒破碎有重要的影响。随着动应力幅值和加载频率的增加,各粒组含量的变化值总体呈现增大的趋势,说明荷载大小和频率对颗粒破碎有明显的影响。从图7中还可以看出,某粒组颗粒破碎导致相邻粒径的粒组和0.075 mm 以下粒组含量增大,这表明颗粒破碎具有连续性。从图8还可以看出,在不同加载次数的循环荷载作用下,粗粒土填料的颗粒破碎具有相似性,但较高振次的荷载作用下小于10 mm 的粒径颗粒变化量相对较大,分析表明随着振次增加,粗粒土的颗粒破碎方式将以破裂、研磨为主。
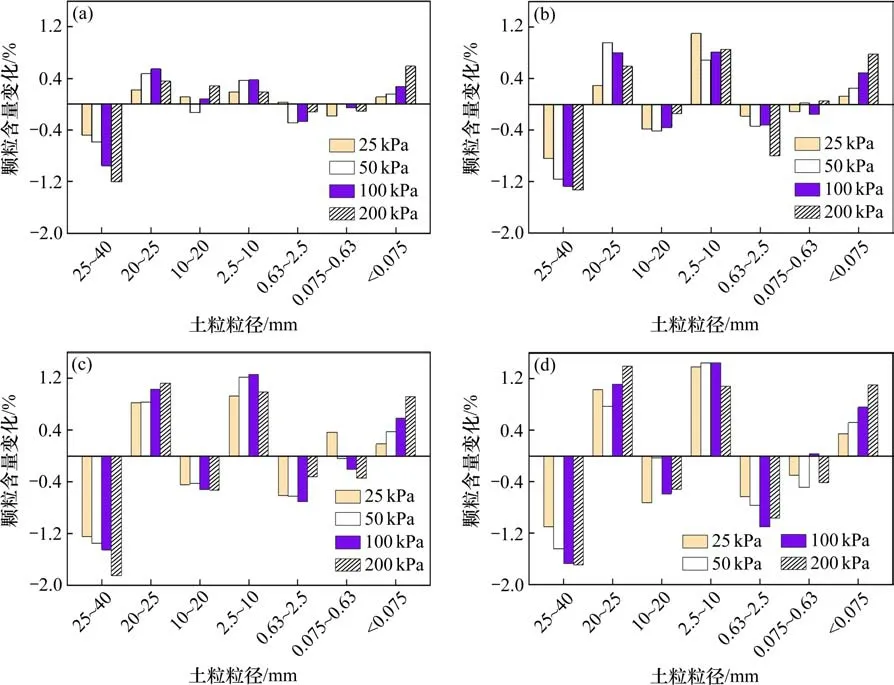
图7 A(1-16)试样颗粒含量变化Fig.7 Variation of sample particle content of group A(1-16)
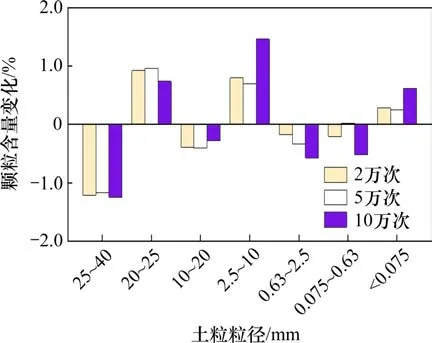
图8 C(1-3)试样颗粒含量变化Fig.8 Variation of sample particle content of group C(1-3)
为了进一步分析动力循环荷载作用下粗粒土填料的颗粒破碎,采用Marsal 提出的颗粒破碎度量指标Bg对试样进行分析。破碎指标Bg表达式如式(1)所示,即将试验前某粒组的百分含量减去试验后相同粒组的百分含量的所有正值累加[9]。
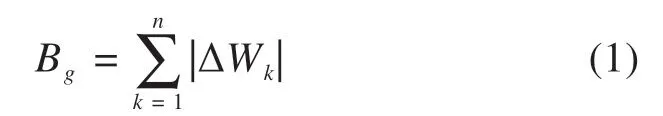
式中:ΔWk=Wki−Wkf,Wki表示试验前级配曲线上某级粒组的含量,Wkf表示试验后级配曲线上相同粒组的含量。
根据图7计算得到动力循环加载试验后,粗粒土填料的颗粒破碎指标Bg如表2所示。
从表2可以看出,在动应力幅值相同时,粗粒土填料的颗粒破碎量随着加载频率的增加而增加;在加载频率相同时,粗粒土颗粒破碎量随着动应力幅值的增加呈先快速增加而后趋于平缓的趋势,这是由于大粒径颗粒破裂成较小粒径后,土体中孔隙被填充而逐渐密实,此时土颗粒间滑动摩擦力作用增强,相互咬合作用减弱,粗颗粒破裂效应减小,研磨效应增加。
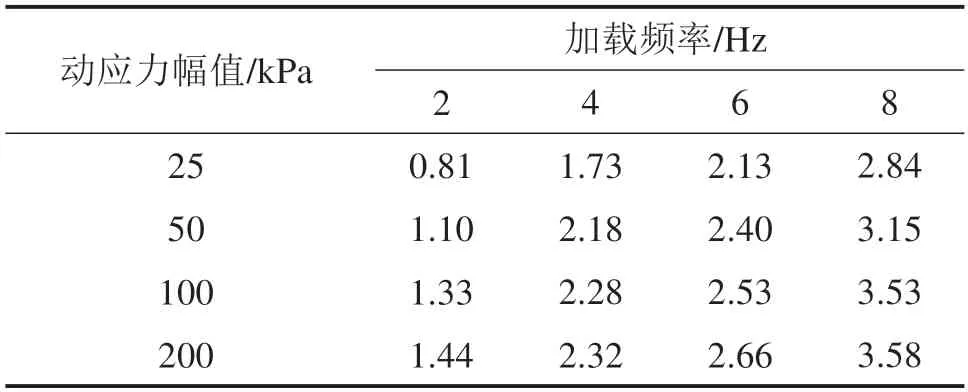
表2 不同条件下的颗粒破碎指标Table 2 Particle breakage index under different conditions
2.3 降雨入渗条件下试样颗粒破碎特征
在降雨入渗条件下粗粒土填料各粒组的颗粒含量变化情况如图9所示。
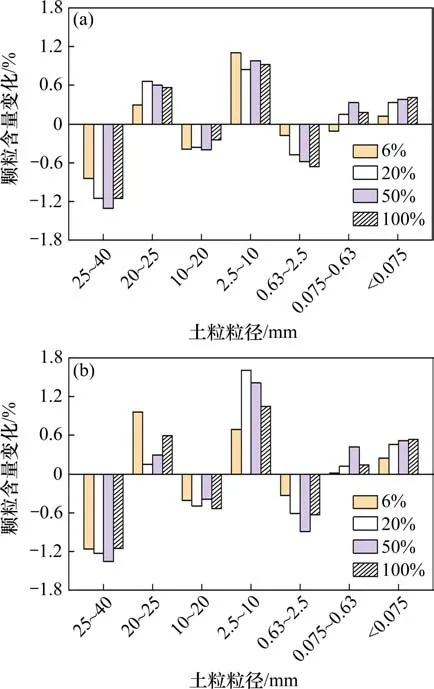
图9 B(1-8)试样颗粒含量变化Fig.9 Variation of sample particle content of group B(1-8)
由图9可以看出,降雨入渗后,在列车荷载作用下B(1-8)试样的粒组含量变化情况与A(1-16)试样基本相同,颗粒含量减小的粒组主要集中在粒径为25~40 mm,10~20 mm,0.63~2.5 mm,增加的粒组主要集中在粒径为10~25 mm,2.5~5 mm,小于0.63 mm 的颗粒。随着降雨入渗强度的增大,粗粒土填料的部分粒组含量变化呈现明显的波动。
为进一步分析降雨入渗对粗粒土填料颗粒破碎特性的影响,利用图9计算得到颗粒破碎指标Bg与降雨入渗强度的关系可由图10表示。
从图10 可以看出,在动应力幅值一定时,粗粒土填料的颗粒破碎量随着降雨入渗强度的增加呈现先增大后减小的现象。其原因可解释为:当降雨入渗量在0%~44%范围内增大时,由于大量雨水从试样的底部渗出,粗粒土填料中大部分区域仍处于非饱和状态,但颗粒之间变得润滑,从而引起摩阻力减小,粗粒土更容易趋于密实,有效接触压力增大,破碎程度逐渐增大;当降雨入渗量在44%~94%范围内增大时,雨水仍会从试样底部渗出,但粗粒土填料部分区域已经达到饱和状态,颗粒间逐渐充满孔隙水,摩擦力进一步减小,部分振动冲击能被孔隙水耗散,同时粗粒土试样中的饱和区在循环荷载作用下孔隙水压力上升,促使细颗粒迁移,引起土体结构更容易破坏,导致粗粒土试样变形虽然增大,但是颗粒破碎效应逐步降低。
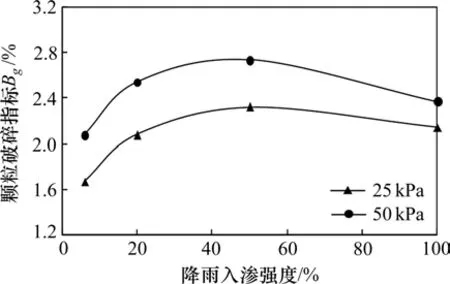
图10 颗粒破碎指标Bg与降雨入渗量关系曲线Fig.10 Curves of relationship between Bg and rainfall infiltration
2.4 颗粒破碎过程分析
利用压实试验模拟粗粒土路基填筑过程,利用动力加载试验模拟列车荷载对粗粒土填料的动载作用过程。粗粒土填料的全过程颗粒破碎指标Bg变化如图11和图12所示。
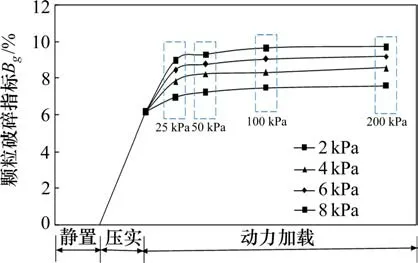
图11 全过程颗粒破碎指标Bg变化Fig.11 Variation of Bgduring the whole process
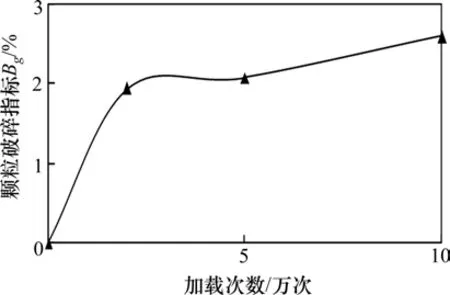
图12 不同加载次数下颗粒破碎指标Bg变化Fig.12 Curves of relationship between Bg and N
由图11 可以看出,在粗粒土填筑、列车运行过程中,粗粒土填料的颗粒破碎指标Bg逐渐增大,且随着动应力幅值的增加而增大并逐步趋于稳定,随加载频率的增加而明显增大。粗粒土填料填筑过程中的颗粒破碎率占总破碎率的50%以上。在相同频率的荷载作用下,粗粒土填料颗粒破碎指标Bg随动应力幅值变化较为平滑,说明粗粒土颗粒破碎随荷载大小呈渐进式变化趋势。在粗粒土路基填筑过程,颗粒破碎方式以破裂、破碎为主,大颗粒破碎形成较小粒径的颗粒,孔隙被填充,但此时路基填料中存在较大的孔隙,经过5万次动力循环荷载后,孔隙进一步被填充,土体趋于密实,粗粒土颗粒破碎方式以破裂、研磨为主,研磨效应逐渐增强。分析表明,粗粒土填料在填筑与列车运行过程中,颗粒破碎方式由破裂、破碎逐渐转为破裂、研磨。
从图12 可以看出,当加载次数在0~2 万次范围内增大时,粗粒土填料的颗粒破碎指标Bg显著增加;当加载次数大于2万次,随着加载次数的增大,粗粒土填料的颗粒破碎指标Bg呈缓慢增加的趋势。由此可以推测,高速铁路粗粒土路基颗粒破碎效应主要集中在运营早期。
3 颗粒破碎分形特性
3.1 颗粒破碎分形分析
由于颗粒破碎指标Bg不能从整体上反映粗粒土填料颗粒级配的调整,为此,学者提出采用分形理论对岩土体颗粒或孔隙进行分析[16],并采用分形维数D来表征粗粒土颗粒发生破碎的程度[7],其分形模型可表示为:
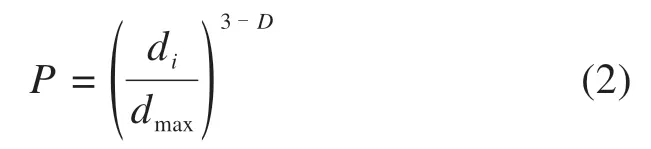
式中:P为粒径为di的颗粒的通过质量百分率;dmax为最大粒径;D为分形维数。
由此可以计算得到压实后粗粒土填料的分形维数平均值为2.636 3,得到动力循环加载试验后A(1-16)试样的分形维数如图13 所示,B(1-8)试样的分形维数如图14所示。
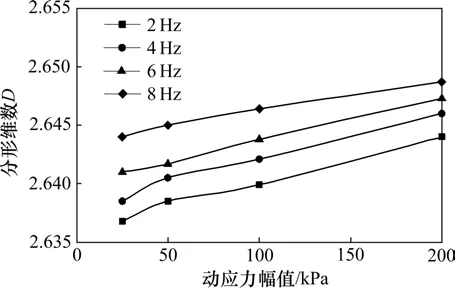
图13 分形维数与动应力幅值、加载频率关系曲线Fig.13 Curves of dynamic stress amplitude,loading frequency and fractal dimension
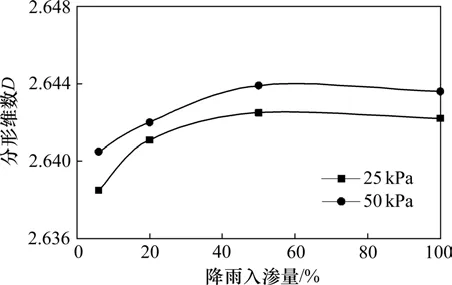
图14 分形维数D与降雨入渗强度关系曲线Fig.14 Curves of relationship between D and rainfall intensity
从图13 中可以看出,随着动应力幅值、加载频率的增大,粗颗粒发生破碎,分形维数逐渐增大,且荷载越大、频率越高,颗粒破碎程度也越大。
从图14可以看出,随着降雨入渗强度的增加,粗粒土的分形维数呈先快速增加而后缓慢减小的趋势。
在动力循环加载试验后,A(1-16)试样粗粒土填料的粒度分形维数D值与颗粒破碎率Bg之间的关系,如图15所示。
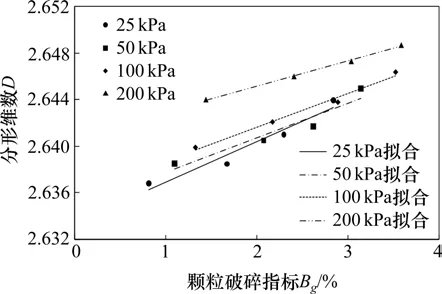
图15 颗粒破碎指标Bg与分形维数D的关系曲线Fig.15 Curves of relationship between Bg and D
由图15 可以看出,在动应力幅值相同时,粗粒土填料的分形维数D与颗粒破碎指标Bg之间存在线性拟合关系,拟合相关系数分别为0.949,0.914,0.985 与0.998。随着动应力幅值的增加,粗粒土颗粒破碎分形分布特征更加明显,分形维数D与颗粒破碎指标Bg间的线性拟合相关系数也越大,二者存在一定的内在联系。
3.2 基于分形维数的粗粒土颗粒破碎率
由上述分析可知,分形维数可以反映粗粒土颗粒级配的变化。因此,本文利用试样加载前后分形维数的差值来表征颗粒破碎程度[13]:

式中:ΔD为动力加载前后粗粒土分形维数的差值;D为动力加载后粗粒土分形维数;D0为动力加载前粗粒土分形维数。
根据式(3)计算得到不同动应力幅值、加载频率条件下的粗粒土以分维数表示的颗粒破碎指标ΔD,如表3所示。
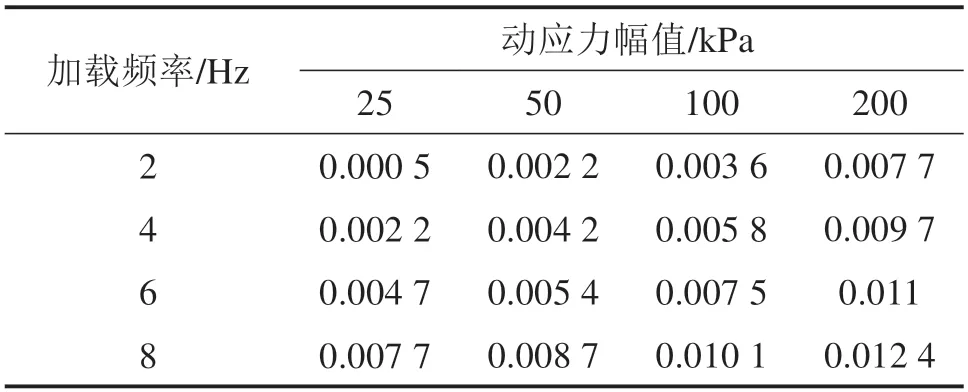
表3 动力循环试验后颗粒破碎率ΔDTable 3 Fractal dimension ΔD value after the test
结合表3 和图12 可知,动力加载后粗粒土填料的分形维数大于动力加载前的数值,且采用分形维数表示的颗粒破碎率ΔD与颗粒破碎Bg相对应。随着动应力幅值、加载频率的增大,粗粒土填料的颗粒破碎率呈非线性增大的趋势,即颗粒破碎效应增强。
3.3 颗粒破碎指标ΔD与累积应变的关系
在动力循环荷载作用下,粗粒土填料的颗粒破碎与其累积残余变形有关,且随累积残余变形的增大而增大[13]。由动力循环加载试验得到高速铁路路基粗粒土填料累积应变ε与动应力幅值、加载频率关系曲线如图16所示。
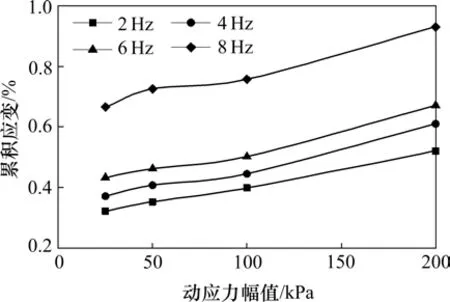
图16 累积应变与动应力幅值、加载频率关系曲线Fig.16 Curves of relationship between cumulative strain and dynamic stress amplitude
可以看出,在动力循环荷载作用下,粗粒土填料的累积应变随动应力幅值、加载频率的增加而增大。通过对数据进一步分析,采用幂函数开展二元非线性回归分析,可以构建累积应变与σdmax,f的关系函数:
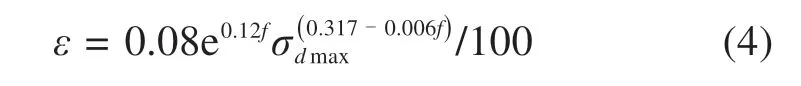
根据图16和表3,可绘制粗粒土填料的颗粒破碎指标ΔD与累积应变ε的关系曲线,如图17所示。
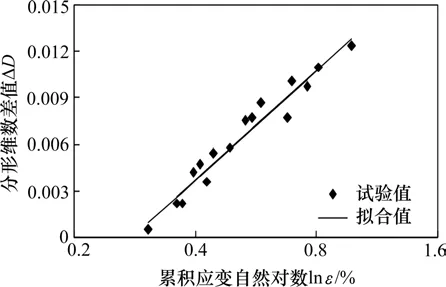
图17 颗粒破碎指标ΔD与累积应变的关系曲线Fig.17 Curve of relationship between ΔD and cumulative strain
通过对图形分析,发现颗粒破碎指标ΔD与累积应变ε的关系如下:

式中:a,b为拟合参数,a=0.01,b=0.06,相关系数R2=0.952。可以看出,动应力幅值越大、加载频率越高,粗粒土填料动力累积应变越大,颗粒破碎率也越大。利用式(4)可以计算得到粗粒土填料以分形维数表征的颗粒破碎率指标最大值ΔDmax为0.06,这反映了动力循环荷载作用下粗粒土填料颗粒破碎的有界特征。
将式(4)代入式(5),可得到颗粒破碎指标与动应力幅值、加载频率的关系如下:
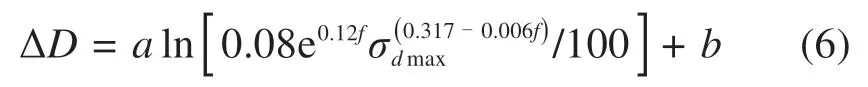
为验证模型的准确性,利用式(6)计算粗粒土填料的颗粒破碎指标,并与试验值进行对比,如图18所示。
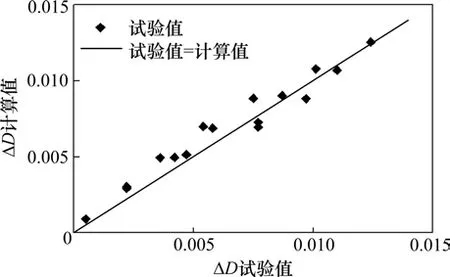
图18 颗粒破碎指标ΔD计算值与试验值对比Fig.18 Comparison of calculated value and test value of ΔD
从图18可以看出,试验值与预测值基本在y=x附近,说明粗粒土填料的颗粒破碎计算模型较合理,能够反映列车荷载作用下粗粒土路基的颗粒破碎性。
根据当前高速铁路路基承受动荷载特征,利用式(6)计算粗粒土路基承受动应力幅值为0~200 kPa,频率为2~10 Hz 的荷载时,颗粒破碎指标ΔD变化规律如图19所示。
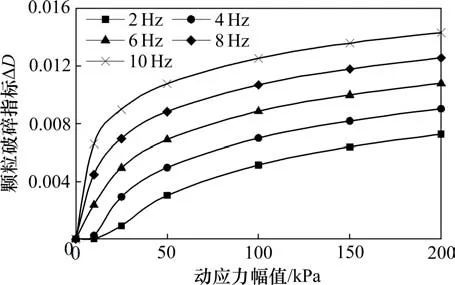
图19 粗粒土路基颗粒破碎变化规律Fig.19 Variation rule of particle breakage of coarse-grained soil subgrade
可以看出,粗粒土路基的颗粒破碎指标ΔD随动应力幅值呈先迅速增加而后缓慢增大的趋势,随加载频率的增大而持续增加。粗粒土路基的颗粒破碎指标ΔD在0~0.014之间。
4 结论
1) 在填筑过程中,粗粒土填料颗粒破碎方式以破裂、破碎为主,研磨为辅。在列车荷载作用下,粗粒土填料的颗粒破碎方式以破裂、研磨为主,破碎为辅。粗粒土填料的颗粒破碎具有相似性和连续性特征。
2) 颗粒破碎指标Bg,分形维数D随着动应力幅值、加载频率的增加而增大,随着振动次数的增加呈先迅速增大而后缓慢增加的趋势。分形维数D与颗粒破碎指标Bg具有良好的线性相关性。
3) 降雨入渗将导致粗粒土颗粒破碎增大。颗粒破碎指标Bg,分形维数D随降雨入渗强度的增加呈先增大后减小的趋势。
4) 利用分形维数差值ΔD作为颗粒破碎指标,建立粗粒土填料颗粒破碎指标与累积应变的关系,讨论了粗粒土填料颗粒破碎的有界性。高速铁路粗粒土路基的颗粒破碎指标ΔD在0~0.014之间。
5) 在路基填筑过程中,应采用低频振动荷载对粗粒土填料进行压实,降低颗粒破碎;在路基使用过程中应尽量减少雨水渗入基床,降低列车荷载作用下粗粒土颗粒破碎,从而减小路基沉降。
