压裂井温度场计算软件设计与实现

张永飞，仝敏波，董斌华，闫钰琦

(延长油田股份有限公司1)定边采油厂，陕西 定边 718600;2)研究院，陕西 西安 710075)

0 引言

压裂技术是石油开采过程中油气井增产、注水井增注的重要技术措施之一［1］。压裂液配方的类型及压裂液返排情况受温度场分布的影响，因此在压裂过程中井下温度场的预测十分重要。

1937年，Schlumberger就开始研究有关测量井筒内流体温度的技术［2］，1962年RameyH利用把油井系统处理成一个无限大圆柱体来离散的思想，提出了符合实际情况的简化井筒传热模型，建立了井筒内温度与井深和生产时间的函数关系式，即著名的Ramey公式［3］。1987年王鸿勋和李平提出了从油管、环形空间以及同时从油管和环形空间注液的新的非稳态井筒传热的计算方法，并将原来的显式计算方法改成了全隐解法，从而保证数值解的无条件稳定。此外还考虑了注入液到达目的层以前，并筒原有积液与并筒、水泥环及地层的热交换。

1969年，Wheeler假设达西渗流滤失速度为常数，将温度视为时间和空间的函数，认为通过热传导和热对流传到裂缝中的热量仪发生在裂缝垂直方向上，并忽略缝宽变化，用缝中热平衡计算温度分布［5］。1984年，Blot等人使用变分法，推导出水力压裂裂缝中的温度分布模式，确定出裂缝扩展期间压裂液温度随着时间和位置的变化情况［6］。20世纪90年代初Kamphluss等人提出了一种考虑了裂缝、滤失带和油层温度分布的数值解法［7］，1996年李青山在李平给出的模型的基础上，考虑了缝高的变化，导出了拟三维裂缝温度场计算模型［8］。

软件设计在前人研究的基础上，依据传热学原理，建立模型并推导模型，实现计算机求解压裂井井筒及裂缝中温度场分布［9］。

1 传热理论与温度场分布模型

传热是由于物体之间存在温度的差异而引起的能量的转移。热量传递有三种基本的方式:热传导、对流换热和热辐射。

①热传导:指两个温度不同的物体或同一物体内部温度不同的各部分，依靠物质内部微观粒子(分子、原子或电子)的运动和碰撞发生的传热过程;

②对流换热:指处于不同温度的物体表面与流体之间发生的传热过程;

③热辐射:指所有物体表面都已电磁波形式辐射能量发生的传热过程。

温度场分布计算模型的建立

在注入压裂液过程中，以井筒及其周围地层为研究对象，整个系统温度变化遵循能量平衡原理:

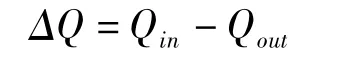
即:单位时间系统内的热量变化=单位时间流入系统的热量－单位时间流出系统热量

将井筒及其周围地层沿径向和纵向划分为一系列的单元体，主要考虑了井内积液、油管壁、油套环空、套管、水泥环、地层的温度分布情况［13］。则上述热平衡方程式适用于每一个单元体的温度研究，综合各单元体，得到如下方程组:

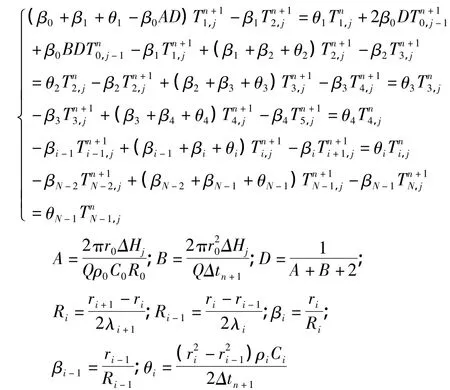
式中 ci－比热，J/kg·°C;ρi－ 密度，kg/m3;λi－导热系数，J/m·min·°C;ri－半径，m;Ti，j－单元体温度，°C;Q—排量，m3/min;Ting－注液温度，°C。

采用“追赶法”［14］求解该方程组。

方程组边界条件为:

2 软件框架设计

压裂井温度场的软件主要是对井筒、裂缝及近缝温度场的计算，通过建立模型及数值模拟，把连续性方程转化成差分方程，应运“追赶法”求解。具体软件设计实现如下:

2.1 压裂井温度场分布研究软件设计的主要模块

①主菜单模块:主菜单模块由井筒温度场分布计算和裂缝及近缝温度场计算两个子菜单组成，主要是选择要进行模式选择。

②数据输入模块:数据输入模块由一个子菜单控制，数据的输入模块控制着计算结果的图形界面。

③模拟计算模块:根据参数输入的数据，计算井筒温度场分布，通过图形或者表格的形式显示出各参数的变化情况。

④数据输出模块:数据的输出模块主要实现程序计算的所有数据存储及输出功能，通过该模块，可以将压裂井温度场分布的数值随输入参数、施工过程中的温度(井筒、裂缝)的变化数据生成文件并显示出来。

2.2 压裂井温度场分布研究软件设计框图

软件框图按照上述思想设计了图1的程序流程图。

2.3 误差分析

此软件的计算值与实测值存在一定的误差，从以下几个方面分析:

①时间步长的影响

在压裂过程中，井筒中的各处温度随时间的变化较大，而在计算中是取许多离散的时间步长，在每个时间步长假定地层传给井筒液体或者井筒液体传给地层的热流速度为恒定的。为了保证精度，时间步长就取得任意小，由于计算机的计算单元的限制，不可能取的任意小。

②热传导系数的影响

地层的热传导系数随着井深是变化的，软件的设计中采用近似值，这给计算结果带来了一定的误差。

③排量的影响

在进行运算的过程中，一直把排量Q看作是恒定的，在压裂施工过程中，排量有些变化，特别是在注液初期更是如此。排量在施工过程中的变化，影响到计算结果。

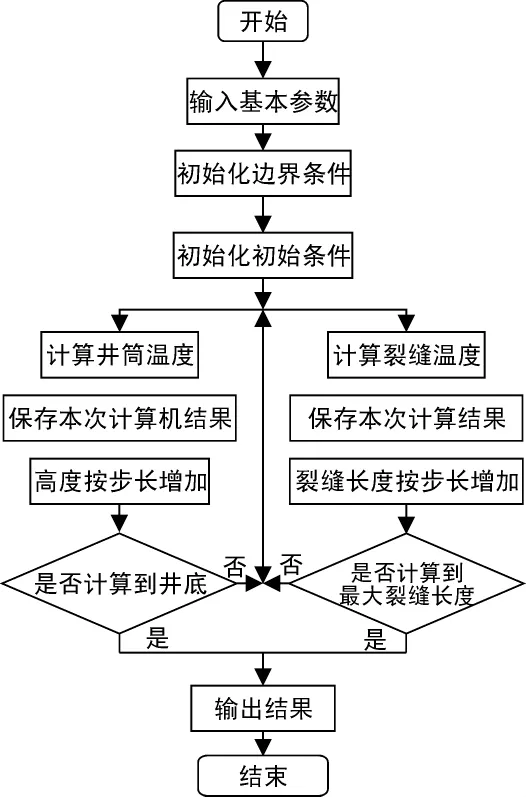
图1 软件程序设计流程图

3 实例应用

本文以GD4井压裂为例。施工前井筒与地层达到热平衡，采用油管注液。施工层段深度:3154.3 m;原始地层温度:110.76°C;原始地温梯度:0.028°C/m;恒温点深度:15 m;恒温点温度:22.86°C;压裂液排量:1.5 m3/min;注液地面温度:16°C;其它基本参数见表1。

表1 GD4井计算参数

根据以上数据模拟计算不同注液量施工层位处油管内温度，不同时刻油管内温度分布、不同排量相同时刻的油管内温度分布及施工层位处油管内不同时刻温度变化情况。

①排量一定不同时刻油管内温度分布(其中Q的单位为m3/min)

利用该井施工数据，模拟计算不同时刻该井油管内温度分布，并绘制了图2不同时刻油管内温度分布曲线进行对比(Q=1.5)。

图2 不同时刻油管内温度分布

从图2中可以看出油管中各点温度随时间增加而下降，施工初期温度下降较快，随着施工的进行，温度下降趋势逐渐变慢，油管内各点温度随着注液时间的增加逐渐接近压裂液地面温度。

②相同时刻不同排量下油管内温度分布

利用该井施工数据，模拟计算不同排量下油管内温度分布。计算结果如下:

i:排量Q=3 m3/min时，计算结果如图3。

图3 排量Q为3时油管内温度分布图

ii:排量Q=6 m3/min时，计算结果如图4。

图4 排量Q为6时油管内温度分布图

计算结果的分析:①不同排量下油管内温度分布排量降低，井筒各点的温度相对略有升高。时间对温度影响较大，施工开始阶段，井筒温度下降较快，而后逐步趋于平缓。到达某一时间，井筒温度趋于不变，即与油层热交换达到平衡。这一平衡温度，决定于排量的大小，排量越大，平衡温度越低，达到平衡温度所需的时间就越短。

②相同时刻不同排量下油管内温度分布

利用该井施工数据，模拟计算不同排量下油管内温度分布，在其它条件相同的条件下。排量越大，压裂液温度升高得越慢。这是因为大排量时，地层传给压裂液的热量一定的基础上，要分配给更多质量的压裂液来使它们的温度升高，因此压裂液的温度升高的较慢些。

4 结论

本文建立的水力压裂过程中井筒及裂缝温度场模型，考虑了井筒积液的影响，采用全三维裂缝延伸模型，能更好地反映裂缝实际情况。软件主要用于计算油井注液过程中井筒温度场与裂缝及近缝地层温度场的分布情况，通过对不同注液条件下，计算温度场的分布。本文设计的压裂井温度场分布计算软件程序，能够精确计算、准确预测井筒及裂缝温度场分布情况，且能够通过绘图直观的说明温度随时间、井深及裂缝长度的变化情况。压裂井温度场分布计算软件设计时主要依据成熟理论模型，在区域地质特征差异方面的影响仍需做进一步研究，提高软件的适用范围。

［1］王晓泉，陈作，姚飞.水力压裂技术现状及发展展望［J］.钻采工艺，1998，21(2):28－32.

［2］Hasan A R，Kabir C S.Heat transfer during two－phase flow in well bores［M］.SPE22948，1991:695－708.

［3］Ramey H J.Well bore J.Heat transmission［M〛.JPT1962:427－435.

［4］王鸿勋，李平.水力压裂过程中井筒温度的数值计算方法［J］.石油学报，1987，8(4):91－99.

［5］Wheeler J A.Analytical calculations of heat transfer from fractures［M］.SPE2494，Improved Oil Recovery Symposium，1962.

［6］ Blot M A.Temperature analysis in hydraulic fracturing［M］.SPE13228.

［7］Kamphuls H，Davies D R，Rood hart L P.A New stimulation for the calculation of the In—situ temperature profile during well stimulation fracturing treatment［J］.The Journal of Canadian Petroleum Technology:1993，32(5):38－47.

［8］李青山.水力压裂裂缝三维延伸数值模拟研究［M］.四川南允:西南石油学院，1996.

［9］杨世铭.传热学［M］.北京:高等教育出版社，1998:1－38.

［10］张琪.采油工程原理与设计［M］.东营:石油大学出版社，2002，282－287.

［11］吴详迪，刘忠春.水力压裂垂直裂缝形态的数值模拟［J］.石油钻采工艺，199l，13(4):34－45.

［12］张平，赵金洲，郭大立.水力压裂裂缝三维延伸数值模拟研究［J］.石油钻采工艺，1997，17(3):53－58.

［13］王洪勋，张士诚.水力压裂水力设计数值计算方法［M］.石油工业出版社，1998，79－1.

［14］同登科，周生田，吴爱弟.计算方法［M］.东营:石油大学出版社，2000:56－57，126－141.