推进器激励船舶振动辐射声计算方法

谢基榕，徐利刚，沈顺根，吴有生

（1中国船舶科学研究中心，江苏 无锡 21408；2军代表室，江苏 无锡 214061）

推进器激励船舶振动辐射声计算方法

谢基榕1，徐利刚2，沈顺根1，吴有生1

（1中国船舶科学研究中心，江苏 无锡 21408；2军代表室，江苏 无锡 214061）

文章在铁木辛柯梁的基础上，建立螺旋桨、轴系及船体耦合振动的数学物理模型，采用声极子模型计算各船体截面振动引起的辐射声压。计算分析了激励力直接作用到船体和经螺旋桨、轴系激励船体振动产生声辐射的差别，指出轴系振动对螺旋桨激励力激起船体振动并产生声辐射有着关键的影响作用。

推进器激励；船体振动；轴系；噪声

1 引 言

潜艇螺旋桨工作于非均匀艉流场中，除了提供推力驱动潜艇前进外，还产生不定常激励力作用到艇体结构上，是引起艇体振动的一个重要激励源。螺旋桨通过轴系激励艇体振动引起的辐射噪声是潜艇水下航行辐射噪声的重要组成部分，国外很早就在这方面开展了研究[1-2]，建立了相关计算方法和控制措施。

近年来这一问题又得到学者关注，Pan[3]首先在实验室台架上设计了包括桨、轴、轴承及推进电机的试验模型，以支撑平板模拟推力轴承安装基座，研究了螺旋桨纵向激励力通过轴承到推力轴承支撑结构的传递机理。在研究中，假定在关心的频率范围内轴系作刚体运动，使用现场测试方法测量了螺旋桨激励力及推力轴承刚度。通过测试认为，推力轴承中的液膜刚度与轴系转速有关并随频率变化。Caresta[4]在其研究中以两头锥段加中间圆柱体（带横隔壁）模拟潜艇艇体，考虑螺旋桨的纵向激励力通过轴系及主推力轴承传递到艇体。采用解析方法分析了结构振动及辐射声场，并应用半数值方法计算比较了轴系偏离艇体中心情况下的激励力到辐射声场的传递函数。

在Goodwin[5]研究的基础上，Dylejko[6]在其研究模型中包括了螺旋桨、轴系、推力轴承、基座和艇体

等部分，考虑螺旋桨纵向激励力引起艇体纵向振动，对艇体纵向振动采用杆模型，使用四端参数法建立了整个耦合系统的运动方程。然后分别以传递到艇体的激励力和功率为控制目标，研究了轴系共振改变器（Resonance Changer）的参数优化设计，共振改变器在本质上也是一个动力吸振器。

Merz[7]研究了考虑螺旋桨激励力的流体传递途径对轴系共振改变器效果的影响。在研究中，建立了包括推进器、轴系及艇体在内的计算模型，艇体模型还包括耐压壳体、横舱壁、舱锥段和前刚性端壁，并使用FEM/BEM方法计算艇体振动响应及辐射声。研究结果表明，在艇体共振频率以上，激励力的流体传递途径降低了共振改变器的减振效果。

国内对螺旋桨、轴系及船体耦合振动并引起辐射声的认识较晚，此前一直认为螺旋桨引起的水下辐射噪声就是螺旋桨直接辐射噪声，并将螺旋桨研究的重点设定在水动力性能及直接辐射声上。在认识到螺旋桨非定常力通过轴系激励船体振动引起水下噪声的重要性后，国内多家单位在该问题上开展了机理分析及控制措施的研究[8-9]。本文针对螺旋桨低频宽带力谱的频率特性，在艇体梁模型基础上，建立了简化的适合工程设计应用的螺旋桨非定常力经轴系激励艇体振动辐射噪声计算方法，在满足工程计算精度的条件下，极大地简化了辐射噪声计算方法。

2 艇体低频振动辐射声计算方法

2.1 推进器经轴系激励艇体振动的数学物理模型

对于潜艇螺旋桨、轴系及艇体耦合振动系统可建立如图1所示的数学物理模型，该模型包括两大部分：船体梁模型和轴系子系统，支撑轴承和推力轴承作为轴系结构的约束条件划归轴系子系统。由于艉流场作用在螺旋桨上的合力具有低频特性，而在低频段0～f1（f1为舱段周向的首阶共振频率）范围内，采用艇体梁模型[10]描述艇体振动便可得到满足工程需求的解。

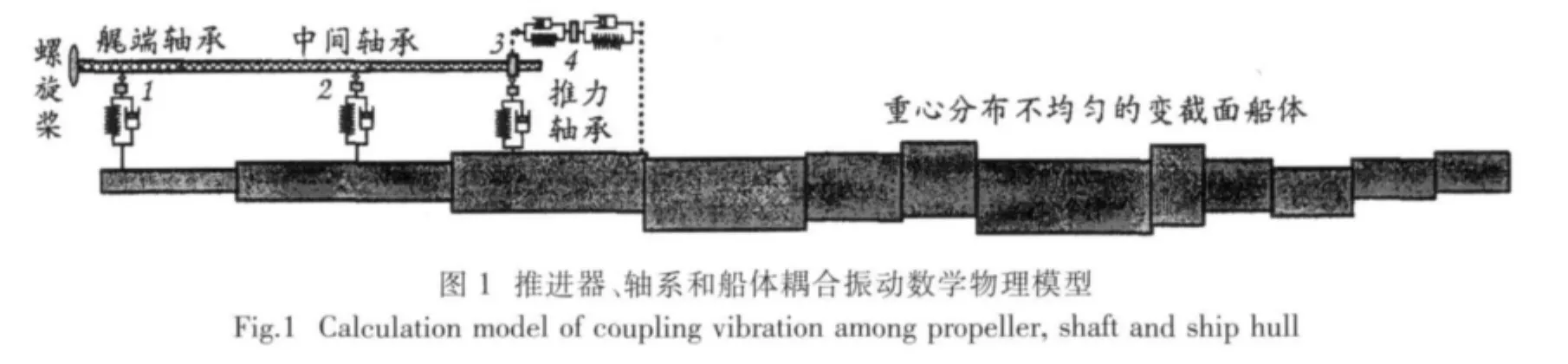
在艇体梁模型中，船体结构被当作截面不发生变形的变截面梁结构。由于实际船体结构在各截面处的弯曲刚度中心与质心不重合，因此，垂直面内的弯曲振动与纵向振动耦合，而水平面内的弯曲振动与扭转振动耦合，从而，需对此两组无法解耦的振动进行同时求解。

在推导艇体梁的刚度矩阵和质量矩阵时，把参考坐标系的原点建立在刚度中心，因此，当梁单元作垂向弯曲运动时，梁单元截面的转角位移φ将产生明显的纵向位移，如图2a所示。由于截面转角位移本身就是微幅运动，所以由截面转角位移引起的横向位移可以忽略，即只考虑由截面转角位移引起的纵向位移。于是梁单元的实际纵向位移可表示为uc（x）=u（x）+eφ（x），其中e定义为梁单元由刚度中心向下到质量中心的偏移量。同理，当梁单元作水平弯曲运动时，梁的面内转角位移τ将产生质心的横向位移，与梁横向平动产生的横向位移叠加，如图2b所示。则梁的实际横向位移为wc（x）=w（x）+eτ（x）。

应用结构有限元理论，分别将船体梁垂向弯曲和纵向耦合振动、水平弯曲和扭转耦合振动的单元位移向量记为｛ue｝=｛u1w1φ1u2w2φ2｝T，｛ue｝=｛τ1w1φ1τ2w2φ2｝T，并将梁单元内部的横向位移和转角位移表达成梁单元节点的二次多项式关系，将纵向位移表示成节点位移的线性关系，从而可以得到任意节点位移下的梁单元应变势能和动能，进而得到梁单元的刚度和质量矩阵。以垂向弯曲与纵向振动耦合为例，梁的单元应变势能与动能可分别表示为：

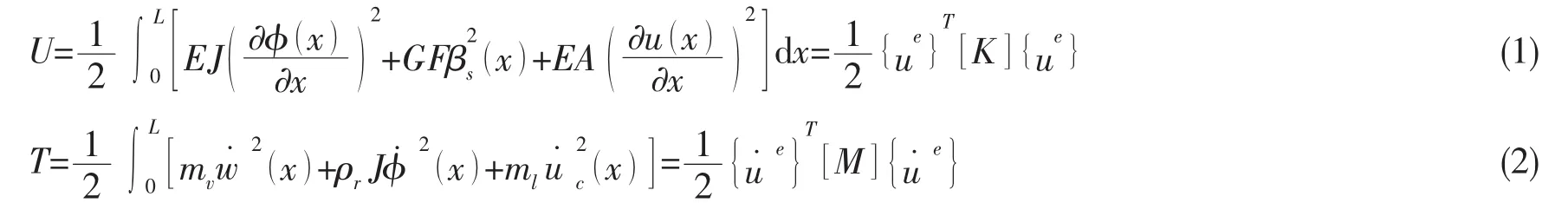
式中，EJ，GF，EA分别为梁抗弯、抗剪切和抗拉压刚度，βs为梁截面剪切变形，mv，ml分别为梁单元作垂向平动和纵向平动时考虑流体附加质量后的等效质量，J为梁单元弯曲运动的转动惯量。从而可以得到梁单元作用于垂向弯曲与纵向耦合振动时的刚度矩阵K和质量矩阵M。

在低频段，连接轴系结构与艇体之间的轴承装置可以使用等效的阻尼弹簧模拟。对于径向支撑轴承，考虑横向刚度，在轴系与艇体间起弯曲振动的耦合作用；主推力轴承同时具有横向刚度和纵向刚度，其在轴系与船体间起到弯曲振动及纵向振动的耦合作用。忽略各轴承装置的不同运动方向的耦合作用。

对船体和轴系分别划分梁单元，并根据前述方法分别计算船体梁单元和轴系梁单元的刚度矩阵和质量矩阵，其中在计算船体梁单元质量矩阵的横向运动分量时将计入流体附加质量的影响[11]；船体结构阻尼以复刚度形式表示，船体梁单元刚度矩阵形式示为（1+jη ）［Ki］。然后，在由艏到艉将船体梁单元和轴系梁单元的节点逐个编号，并分别将船体梁单元和轴系梁单元的刚度、质量矩阵填入对应自由度，从而组装形成总体刚度阵［K］和总质量阵［M ］，针对分析频率计算得广义刚度矩阵［K］G=［K］-ω2［M ］。再将用于描述各轴承动力特性的阻抗参数换算到等效刚度并分别叠加到广义刚度矩阵［K］G中，即可得到描述螺旋桨、轴系及船体耦合振动的结构有限元广义刚度矩阵。再考虑流场作用在螺旋桨上的激励力，从而得到包括螺旋桨、轴系系统和船体结构在内的全系统振动方程组［K］G｛u｝=｛F｝，完成方程组求解后即可得到螺旋桨、轴系与船体结构耦合振动的位移解。

2.2 艇体梁模型的辐射声计算方法

针对推进器、轴系及艇体耦合振动具有低频特性，此频率段内的声波波长远大于船体截面的尺度，因此，无论是弯曲振动还是纵向振动，艇体梁单元的声辐射都满足声致密条件，因而可以使用声极子模型计算各艇体截面振动引起的辐射声压[12]。

船体水下振动声辐射在辐射机理上可分解为两部分，并分别使用不同声辐射模型计算。船体弯曲振动引起船体段元在水介质中横向平动且不产生船体截面变化，因此可用偶极子模型计算[12]各梁单元的引起辐射声压。

式中，S，w分别为梁单元的横截面积和弯曲横向位移，r，ω，k分别为声场点距离、分析圆频率和声波数，θ，φ分别为声场点与艇轴线的夹角和声场点艇轴线所在平面与垂直面的夹角。

当船体作纵向振动时，纵向运动经泊松效应引起截面变化产生体积变化，截面变化部位（含艏、艉端部）的纵向运动也将产生局部的体积变化，见图3所示，其中a（x）为各截面处的艇体平均半径，阴影面积部分表示艇体纵向振动引起的局部体积变化。因此，可用单极子模型计算因船体纵向振动引起的水下辐射声压级，三部分体积变化产生的辐射噪声总和为式中，S，u分别为梁单元的横截面积和纵向弯曲横向位移，θ为声场点与艇轴线的夹角，纵向振动产生声压与声场点在艇体横剖面上的方位角无关。

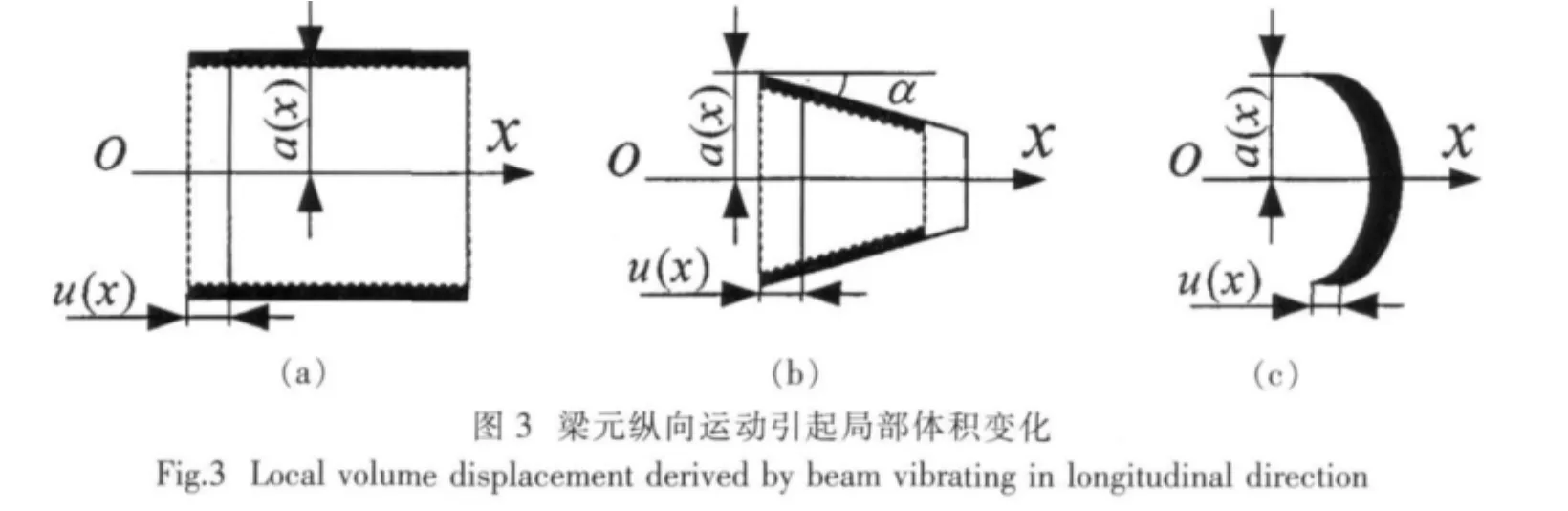
当不同激励力间不存在固定相位差时，其振动响应及后续的声压也不具有固定的相位差，因此，多激励力引起的辐射声场也不存在稳定的干涉作用，从而适合使用能量叠加方法计算由两方向振动引起的总辐射声压级。在本文中，由于考虑了因质量中心偏离刚度中心引起的纵向振动与垂向弯曲振动的耦合作用，所以单独纵向激励将引起垂向弯曲振动，反之亦然。由同一激励力引起的纵向振动和垂向弯曲振动存在确定相位差关系，因此，由此两振动分量引起的辐射声场也将存在稳定的相位差关系，从而应使用场点声压复幅值相加的方法叠加此两振动分量引起的辐射声。同时，由不同激励力引起的船体振动辐射噪声仍使用能量叠加方法计算总辐射声压级。

3 计算结果及分析

以典型船体为例，从设计方案中提取船体梁模型参数，参考全船平均质量中心在其刚度中心以下0.3m处，根据各船舱的功能初步分配各舱质量中心的不同分布，并取单位力作为螺旋桨处的非定常激励，分析轴系到船体的力传递特性和船体的声辐射特性。

图4给出了单位力直接激励艇体产生的辐射噪声，图例“纵向/垂向振动辐射声”表示不考虑弯纵耦合情况下的艇体辐射声，从中可以看出在平均质量中心偏离刚度中心e=0.3m情况下，弯纵耦合引起的辐射声压变化很小，尤其对纵向激励力作用下的耦合更是可以忽略。而在垂向激励力作用下，艇体首阶纵向振动固有频率附近引起的耦合纵向振动比较明显，耦合振动对辐射声压的增强达到10dB，但对宽频带上的辐射总声压贡献却很小。因此，在工程设计计算中可以忽略弯曲振动与纵向振动的耦合影响。

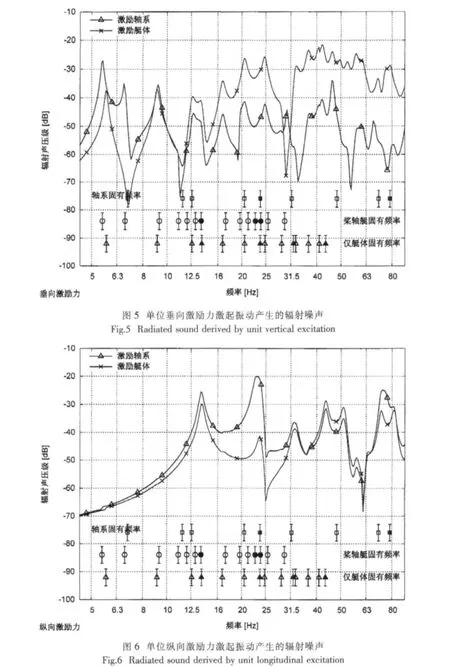
从图5和图6所示计算结果中可以看出，轴系子系统的纵向振动对螺旋桨纵向激励力激起船体振动并产生辐射声有决定性的影响作用，在轴系子系统第一阶纵向固有频率附近，使辐射声频谱增强30～40dB；在大于轴系子系统纵向第一阶固有频率的频段上，轴系子系统使传递到船体的纵向激励力减小，降低了船体振动辐射声压，轴系子系统纵向二阶固有频率已经超出螺旋桨低频宽带激励力的有效频率范围，可以不关心轴系二阶振动对纵向力传递特性的影响。同时，轴系子系统在其前两阶弯曲振动固有频率处对螺旋桨非定常力激励船体弯振动的影响也很大，尤其在轴系第一阶弯曲固有频率上可增强船体辐射噪声达到20～30dB，同样地，在高频段（轴系三阶弯曲振动固有频率以上）轴系对横向激励力也有衰减作用。因此，分析和优化轴系子系统的首阶纵向振动和前两阶弯曲振动的固有特性将是评估和控制螺旋桨经轴系激励船体振动辐射噪声的关键工作。

4 讨 论

4.1 船体梁模型适用性

螺旋桨经轴系激励船体振动产生辐射噪声具有低频特性，与之相应地，也只需要考虑低频范围内的船体动力响应特性。因此，船体梁模型成为分析工作的优先选择，并使用声单极子、偶极子模型计算船体梁振动引起的辐射声场。但由于螺旋桨激励力频率范围又略超过船体舱段首阶固有频率，因此一直以来，使用船体梁模型研究螺旋桨、轴系及船体耦合振动噪声问题存在某些争议。

Caresta[4]在其研究中，对船体建立了首尾锥段、柱段加横舱壁的简化模型，对周向加强肋进行平均处理，并建立了壳体与平板耦合的运动方程；然后在船体截面处施加均匀纵向力和侧面集中弯矩，此处弯矩激励由轴系偏心引起。研究结果表明，在纵向单位力激励壳体侧壁时，壳体振动响应以周向0阶及1阶模态为主，而周向2阶模态分量很小；在相应的辐射声中，也是壳体周向0阶及1阶模态响应占绝对的贡献地位，在关心的频率范围内可以忽略周向2阶模态的贡献。而壳体周向0阶及1阶模态分别对应于“呼吸模态”和截面不变形的弯曲模态，因此，可以用梁模型描述此两阶模态的振动行为。

Caresta的研究成果将船体梁模型的适用频率范围上限拓展至船体第二阶周向频率以上，间接地证明了应用船体梁模型研究螺旋桨、轴系及船体耦合振动噪声问题的合理性，也为本文的研究工作提供了理论依据。

4.2 轴系减振设计分析

前述计算结果表明，在船体纵向振动固有频率和轴系子系统固有频率处的水下辐射噪声级都比较高。一般而言，船舶结构的固有振动特性很难改变，因此，欲改变螺旋桨经轴系激励船体振动辐射声特性，在激励力特性不变的情况下，只能通过改变轴系子系统参数，来改变实际传递到船体上的激励力。

在轴系子系统中，连接轴系与船体结构的主推力轴承及其基座的动态参数是影响轴系子系统的关键参数，它直接决定了轴系子系统纵向振动的第一阶固有频率和力放大系数。减小主推力轴承纵向动刚度可将轴系子系统的“力放大”范围向低频方向移动，再结合低频振动具有更低的辐射效率，可使得总辐射声得到控制，但此设计过程中需避免轴系子系统的固有频率与船体第一阶纵向固有频率吻合以产生更高的辐射声水平。图7给出了推力轴承纵向动刚度两种取值情况下的辐射噪声比较结果，激励力参考某实船螺旋桨的纵向低频宽带激励的频率特性。

轴系减振设计的第二个着眼点便是降低轴系子系统或船体固有频率处的共振峰值，其有效途径之一便是采用动力吸振器[8,13-14]或位置自适应的主推力轴承，位置自适应的主推力轴承方案仍是建立在降低主推力轴承纵向刚度的基础上，但通过调节主推力轴承在静载荷作用下的平衡位置以提供更低的纵向动刚度。这些复杂的控制措施都还需要更进一步的深入研究。

5 结 论

本文针对推进器激励船体振动产生辐射噪声具有低频特性，建立了推进器经轴系激励船体结构振动并产生辐射声的数学物理模型，给出了船体振动响应和辐射声的计算方法，并通过螺旋桨、轴系及艇体耦合振动噪声计算算例，得出以下结论：

（1）垂向激励力作用下需考虑因质量中心与刚度中心偏离引起的垂向弯曲与纵向耦合运动，而纵向激励力作用下则可忽略此耦合因素。

（2）螺旋桨纵向非定常力以轴系激励船体振动产生辐射噪声主要体现为船体首阶纵向振动的强辐射特性和轴系子系统首阶纵向振动的力放大作用，它们是螺旋桨激励船体在低频处产生高辐射噪声水平的主要原因；同时，轴系子系统前两阶弯曲振动也对螺旋桨横向激励力到船体的传递特性有重要影响作用。

（3）控制螺旋桨纵向非定常力激励船体产生辐射声可采用两个基本策略：一是设计更低纵向动刚度的推力轴承支撑系统，以降低轴系纵向首阶共振频率，将其推到辐射声关心的频率范围外；二是使用动力吸振器削弱轴系子系统或船体首阶纵向固有频率处的力传递。

[1]Chertock G.Forces on a submarine hull induced by the propeller[J].Journal of Ship Research,1965,9(2):122-130.

[2]Rigby C P.Longitudinal vibrations of marine propeller shafting[J].Transactions of the Institute of Marine Engineers,1948,60:67-78.

[3]Pan J,Farag N,Lin T,et al.Propeller induced structural vibration through the thrust bearing[C]//Acoustics 2002-Innovation in Acoustics and Vibration.Adelaide,Australia:Annual Conference of the Australian Acoustical Society,2002:390-399.

[4]Caresta M,Kessissoglou N.Low frequency structural and acoustic responses of a submarine hull under eccentric axial excitation from the propulsion system[C]//Acoustics 2008.Geelong,Australia,2008:1-8.

[5]Goodwin A J H.The design of a resonance changer to overcome excessive axial vibration of propeller shafting[J].Institute of Marine Engineers-Transactions,1960,72:37-63.

[6]Dylejko P G.Optimum resonance changer for submerged vessel signature reduction[D].Sydney,Australia:University of New South Wales,2007.

[7]Merz S,Kessissoglou N J,Kinns R.Excitation of a submarine hull by propeller forces[C]//14th International Congress on Sound and Vibration.Cairns,Australia,2007.

[8]曹贻鹏,张文平.轴系纵振对双层圆柱壳体水下声辐射的影响研究[J].船舶力学,2007,11(2):293-299.

[9]谢基榕,沈顺根,吴有生.推进器激励的艇体辐射噪声及控制技术研究现状[J].中国造船,2010,51(4):234-241.

[10]Daidola J C.Natural vibrations of beams in a fluid with applications to ships and other marine structures[J].SNAME transactions,1984,92:331-351.

[11][苏]卡洛特金A N.船舶附连水质量手册[M].圣彼得堡:圣彼得堡船舶出版社,1986.

[12]Junger M C.Sound radiation by resonances of free-free beams[J].Journal of the Acoustical Society of America,1972,52(1-2):332-334.

[13]曾革委.螺旋桨轴系艇体半主动控制仿真[C]//崔维成.2005年船舶结构力学学术会议论文集.舟山:《船舶力学》编辑部,2005:519-523.

[14]刘耀宗,王 宁,孟 浩.基于动力吸振器的潜艇推进轴系轴向减振研究[J].振动与冲击,2009,28(5):184-187.

Calculational method for radiating sound excited by vibration of ship propeller

XIE Ji-rong1,XU Li-gang2,SHEN Shun-gen1,WU You-sheng1
(1 China Ship Scientific Research Center,Wuxi 214082,China;2 Army Deputy,Wuxi 214061,China)

Based on Timoshenko beam model,the calculation model of coupling vibration of propeller,shaft and ship hull is established in this paper,and the sound pressure derived by hull vibration is calculated with monopole or dipole model.Difference between the sound derived by hull vibration induced propeller excitation directly acting on hull and that acting on shaft is also analyzed,and therefore the effect of shaft on propeller excitation transmission to hull is demonstrated.

propeller excitation;ship hull vibration;shaft;noise

TB53 U661.44

A

1007-7294（2011）05-0563-07

2011-03-02

谢基榕（1978-），男，博士研究生，主要从事舰船振动声辐射理论研究和试验研究。