随机风浪中舰船横摇倾覆概率分析

施兴华，张 婧，王 善

（1江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2哈尔滨工程大学 建筑工程学院，哈尔滨 150001）

随机风浪中舰船横摇倾覆概率分析

施兴华1，张 婧1，王 善2

（1江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003；2哈尔滨工程大学 建筑工程学院，哈尔滨 150001）

以路径积分法为基础，采用Gauss-Legendre公式探讨了随机风浪作用下舰船的运动及其倾覆概率计算。考虑阻尼力矩、复原力矩的非线性及风浪的随机性，建立了随机风浪中舰船运动的非线性微分方程，应用路径积分法给出白噪声随机扰动和定常风倾力矩作用时横摇角概率密度函数随时间的演变，按照现有的倾覆准则给出舰船倾覆概率的表达式。通过算例，验证了路径积分法的准确性，分析了各个参数对横摇角概率密度的影响，计算得出了不同风速、不同航速下的倾覆概率，以及倾覆概率随时间的变化。研究表明，此方法简便可行，并能在数量上预报舰船在随机风浪下的倾覆概率。

随机风浪；横摇倾覆概率；路径积分法；Gauss-Legendre公式

Gauss-Legendre formula

1 引 言

舰船倾覆是造成人员及财产重大损失的严重事件，历来受到造船界与航运界的极大重视。舰船在海浪中的运动涉及到外载荷的随机性和舰船运动的非线性。外载荷是由风、浪等联合引起的,具有一定的随机性，这就导致舰船的倾覆是具有一定概率的随机事件。确定该随机事件的发生概率，对工程实际具有一定的参考价值。

非线性大幅横摇是导致海浪中舰船倾覆的主要原因。目前，国内外的不少学者基于动力学的理论和方法，对规则波及随机波激励下的船舶非线性横摇运动与船舶倾覆概率进行了研究，希望能够解释随机海浪中船舶倾覆机理[1-6]。但这些方法只考虑了海浪的随机性，而且许多学者认为，定常力矩的存在将大大降低舰船的稳性。为此，本文综合考虑了船舶阻尼非线性、复原力矩非线性以及随机风浪激励，将平均风倾力矩视为定常力矩，建立了横摇随机微分方程，采用理论上较为成熟的路径积分法[7]求解随机微分方程，导出了舰船倾覆概率随时间变化的表达式；分析了各个参数对横摇角概率密度的影响，讨论了不同风速、航速对船舶倾覆概率的影响。算例表明，这种方法比较准确而且简便易行，能够很好地反映横摇过程，对深入探讨船舶在波浪上的强迫非线性运动奠定了必要的基础，可为进一步研究舰船倾覆及稳性横准提供有益的参考。

2 随机风浪扰动力矩

风扰动力矩可以看作是平均值Ma与脉动部分Md（t）两部分组成，其中考虑舰船航速对风速的影响，可得式中：ρ—空气密度；A—舰船结构水线以上部分侧投影面积；Δz—舰船结构水线以上部分侧投影面积的形心至水压力作用点的距离；U（t）—舰船的航速；υd（z,t）—短周期内脉动风速；υa（z）—平均风速[8]；Cm—风压倾侧力矩系数[9]，

式中：A—舰船水线以上部分侧投影面积；L—舰船结构总长；B—舰船横剖面宽度；z—舰船结构水线以上部分侧投影面积的形心至水线的距离。

（3）式充分反应了船型主要因素对风压的影响，其变化范围在0.955～1.418之间，如果Cm取为定值，势必对有些船舶稳性要求过高，而对有些船舶又会显得不足。因此，根据船型选取不同的Cm值是较符合客观实际的。

波浪扰动力矩为

航速U（t）与给定z处的平均风速都是常数，故由（1）式可知，Ma也是一常数。脉动风的强度随时间而随机变化，是典型的随机过程。 由（2）式可知，Md（t）是 υd（z,t）的线性函数，所以可认为Md（t）是平稳正态随机过程。同理，Mw（t）也是平稳正态随机过程。

3 舰船横摇运动微分方程

随机横摇运动的舰船受到惯性力矩、阻尼力矩和回复力矩及环境载荷的作用，故舰船大幅横摇模型可用以下微分方程来描述

4 横摇微分方程的求解

4.1 相应的简化方程

实际随机风浪须处理为有色噪声，理论上来说是可以通过增加滤波系统并利用Markov过程来求解这一复杂的问题，而这样处理后，将会出现高维数的随机微分方程。为了便于讨论，假定风浪为白噪声。在不影响问题结论的基础上，将问题简化为二元，即将（8）式化为

4.2 路径积分法求解FPK方程

路径积分的基本思想就是在空间和时间上分别离散化，以路径和代替积分，即通过连接短时转移概率密度形成全局转移概率密度，得到状态向量的联合概率密度函数。设X→（t）是n维状态方程，其演化概率密度为

Yu[13]等人将（14）式按照Gauss-Legendre积分来离散化，得到基于Gauss-Legendre公式的路径积分法。已知第（i-1） 时刻的每个高斯积分点上的概率密度及相应转移概率密度时，借助离散化的概率密度表达式，可获得第i时刻任意点的概率密度，因此仅需计算第i时刻相应高斯积分点的转移概率密度。这样可大大减少计算量，最终可得到适合编程实现的表达式。对于一维的情况，即

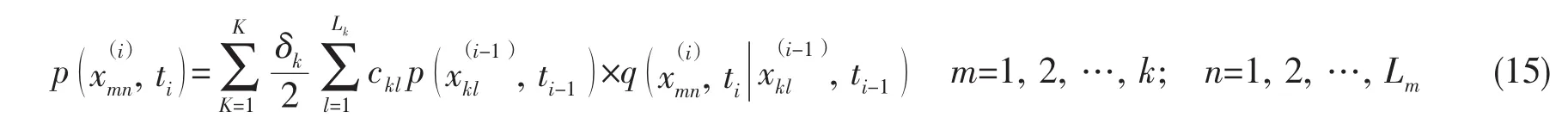
式中：K—子区间数；Lk—第k子区间的高斯积分点数；δk—第k子区间的长度；xkl—高斯积分点；ckl—相应的权数。

一般假设短时转移概率密度是近似高斯分布的。Sun和Hsu[14]提出利用矩方程导出短时转移概率密度的一阶矩和二阶矩，但由于非线性随机系统的矩方程一般是无穷层次、非封闭的，可利用高斯截断法获得封闭的矩方程。因此，短时概率密度可写为

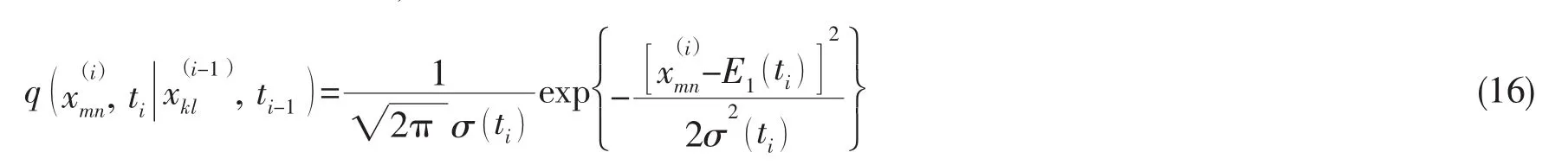
式中：E1（ti）、E2（ti）—ti时刻X的一阶、二阶原点距，可通过封闭的矩方程组[15]解出；σ2（ti）=E2（ti）-［E1（ ti）］2。

5 舰船倾覆概率计算

舰船结构倾覆是由于横摇角过大引起的，当横摇角超过某一阈值之后，就将一直增大下去而永远不会回到平衡位置。舰船的倾覆是一个不可再现的事件，因此不可能用通常的概念来定义倾覆概率。这里定义在任意时刻t，舰船结构的倾覆概率为

式中：p（ φ, ）t—t时刻横摇角的边缘概率密度；φv1—正稳性消失角；φv2—负稳性消失角。

6 计算实例及分析

采用fortran90语言自编程序，对某舰船在初始时刻遭受白噪声风浪及平均风倾力矩联合作用下横摇倾覆进行了分析计算，计算船的主要参数如表1所示。

表1 计算船的主要参数Tab.1 The parameters of ship

如果（9）式中非线性阻尼系数v3=0，定常横倾力矩Xa=0，则该方程有精确平稳解为[13]

式中：C—归一化常数。

图1中（a）为精确平稳解，（b）为用路径积分法所得解（t=100s），两者基本一致，则表明路径积分法能很好地解决这一类随机动力学问题。

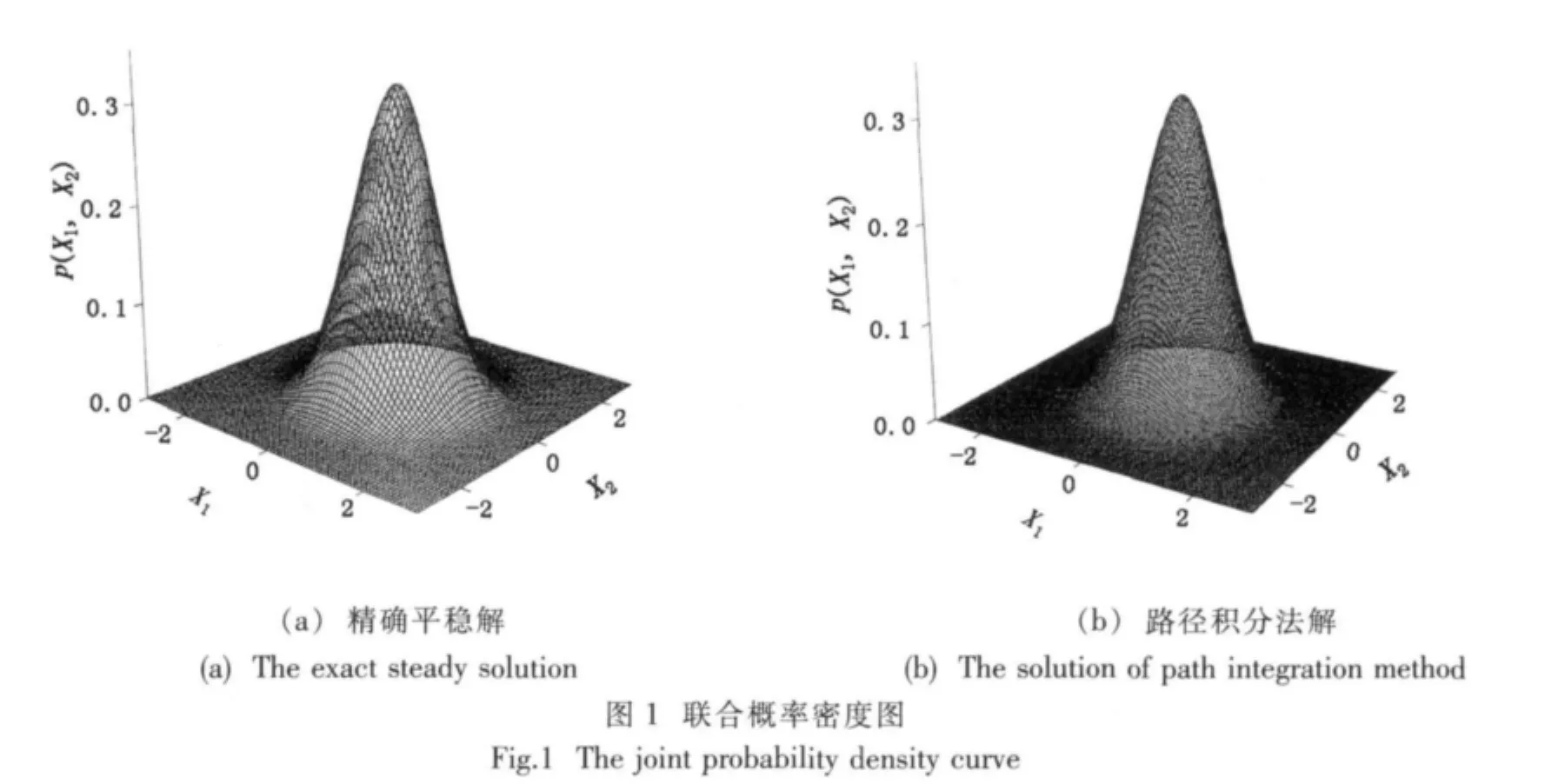
当考虑风速和航速的影响即加入定常横倾力矩及计入非线性阻尼时，该方程没有解析解。这时可采用上述的路径积分法来讨论这个问题，并分析各个参数对横摇角概率密度的影响。

图2为横摇角边缘概率密度随三次回复力矩系数c3变化图。从图中可看出，随着三次复原力矩系数c3的减小，其概率密度峰值逐渐减小，分布的范围变大，即横摇角概率密度的集中程度随着三次复原力矩系数c3的减小而逐渐降低。

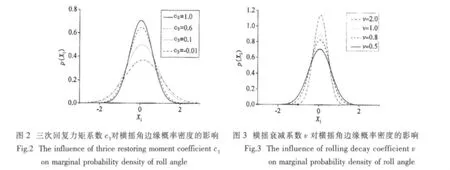
图3、4分别为横摇角边缘概率密度随着随机扰动力矩系数γ、横摇衰减系数v的变化图。由图可知，γ越大，横摇角概率分布的峰值越小，但横摇角的变化范围变大；而对于横摇衰减系数v的增大，其概率分布峰值增大，分布范围减小。上述分析说明γ的增大倾覆概率变大，v增大倾覆概率减小，这与根据稳性所作的直观判断是一致的。

考虑风速和航速对船舶横摇倾覆即定常横倾力矩对横摇响应的影响。图5为va=22.5m/s，U=18kns时舰船横摇角边缘概率分布随时间的演变过程，初始时刻（t=0）横摇角围绕正浮位置分布，但由于计入风速和航速的影响，横摇角则围绕定常力矩引起的倾角分布。由图5可看出，边缘概率密度的峰值随着时间的增长而逐渐减小，但横摇角的分布范围随着时间的增大而增大。

图6给出了航速分别为18kns和32kns时舰船横摇倾覆概率随风速的变化曲线。由图可知，航速和风速的增大均能使舰船的倾覆概率增加。在航速和风速均为最大即va=30m/s，U=32kns时，其横摇倾覆概率达到0.009 54。图7为在va=22.5m/s，U=18kns，舰船倾覆概率随时间的变化曲线，可明显看出，从0-20s倾覆概率不断增大，最大值为0.007 2，在随后的持续时间内趋于平稳值。

7 结 论

本文将基于Gauss-Legendre公式的路径积分法用于对随机风浪中舰船的倾覆概率进行计算分析。由上述理论和实例分析，可得出如下结论：

（1）路径积分法的近似解与精确解结果比较表明，本文的方法在研究随机激励下舰船的非线性横摇运动是非常有效的，能很好地解决舰船在随机风浪联合作用下的倾覆概率问题，也可用于解决其它一些类似的非线性动力问题。

（2）考虑到舰船的结构形式比较特殊，改变传统的处理方法，将风压倾侧力矩系数Cm视为变化量，计入船型因素对风扰动力矩的影响，同时考虑了航速对风速的影响，即风以相对风速的形式作用于舰船，给出了计入航速影响的风扰动力矩计算公式，更符合实际情况。

（3）计算结果表明，舰船的三次复原力矩、随机扰动力矩系数、横摇衰减系数均对横摇角概率分布有一定的影响。横摇角概率密度的集中程度随着三次复原力矩系数c3、横摇衰减系数v的减小而逐渐降低，随着γ增大而降低。

（4）舰船的倾覆概率与风速、航速等因素密切相关，即倾覆概率随着风速、航速的增加明显增大，而且舰船在刚遭受外激作用时，其倾覆概率逐渐增大，随后趋于平稳。这与根据实际情况所作的判断相符，故舰船在航行时，必须根据海域风浪的情况来调节航速以保证其稳性。

（5）本文用白噪声过程代替实际风浪的有色噪声过程，与实际情况相比有一定的误差，而合理的滤波系统可能会改善计算结果，这样必将出现高维方程。因此，高维FPK方程的求解将是一个重要的研究方向。

[1]Jiang C,Troesch A W,Shaw S W.Highly nonlinear rolling motion of biased ships in random beam seas[J].Journal of Ship Research,1996,40(2):125-135.

[2]Taylan M.Static and dynamic aspects of a capsize phenomenon[J].Ocean Engineering,2003,30:331-350.

[3]Thompson J M T.Transient basins:a new tool for designing ships against capsize[C]//Proceedings,IUTAM Symposium on the Dynamics of Marine Vehicles and Structure in Waves.London,1999:325-331.

[4]王冬姣,于 玲.横向规则波作用下的船舶倾覆[J].船舶力学,2004,8(2):25-28.

[5]刘利琴,唐友刚,郑宏宇等.随机横浪中船舶倾覆概率的时域分析方法[J].天津大学学报,2006,39(2):165-169.

[6]袁 远,余 音,金咸定.船舶在规则横浪中的奇异倾覆[J].上海交通大学学报,2003,37(7):995-997.

[7]Wehner M F,Wolfer W G.Numerical evaluation of path-integral to Fokker-Planck equations[J].Physical Review A,1983,27(5):2663-2670.

[8]张相庭.结构风压和风振计算[M].上海:同济大学出版社,1985.

[9]汤忠谷,韩久瑞.海船风压试验研究[J].中国造船,1981(2):31-38.

[10]李积德.船舶耐波性[M].哈尔滨:哈尔滨船舶工程学院出版社,1992.

[11]Haddara M R.On nonlinear rolling of ships in random seas[J].ISP,1973,20:230-231.

[12]Nayfeh A H,Khdeir A A.Nonlinear rolling of ships in regular beam seas[J].ISP,1986,33:40-49.

[13]Yu J S,Cai G Q,Lin Y K.A new path integration procedure based on Gauss-Legendre scheme[J].Int.J Non-Linear Mechanics,1997,32(4):759-768.

[14]Sun J Q,Hsu C S.The generalized cell mapping method in nonlinear random vibration based upon short-time Gaussian approximation[J].Journal of Applied Mechanics,1990,57:1018-1025.

[15]方 同.工程随机振动[M].北京:国防工业出版社,1995.

Analysis of rolling capsizing probability of warship under random wind and beam seas

SHI Xing-hua1,ZHANG Jing1,WANG Shan2
(1 School of Naval Architecture and Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,China;2 School of Civil Engineering,Harbin Engineering University,Harbin 150001,China)

The path integration method based on Gauss-Legendre integration scheme was applied to the motion of ship subjected to random wind and beam seas.Considering the nonlinear damping moment,restoring moment and random wind and seas,the nonlinear differential equation for ship’s rolling motion was established.The rolling angle probability density was analyzed using the path integration method,when the ship was subjected to white noise disturbance and a stationary wind moment,then capsizing probability was also calculated according to the presented rules.The presented method was capable of producing accurate results,which could be proved through the example.At the same time,the influence of each parameter on the probability density was analyzed.Furthermore,the capsizing probability at different velocity of wind and sailing was calculated,and the probability with time was also computed.The study shows that this method is easy to achieve.Thus the rolling capsizing probability of warship in random wind and beam seas could be predicted quantitatively by the proposed method.

random wind and beam seas;rolling capsizing probability;path integration method;

U661.22

A

1007-7294（2011）05-0473-07

2010-12-01

江苏省高校自然科学基金资助项目（10KJB58002）；江苏省重点实验室资助项目（CJ0904）

施兴华（1981-），男，博士，讲师，研究方向：结构可靠性，E-mail:shixinghua9@163.com。