具有等待时间的复杂可修复系统的指数稳定性
2011-01-15陆世炎李全艳金光植
陆世炎,李全艳,金光植*
(1.延边大学理学院 数学系,吉林 延吉133002;2.郑州大学 数学系,河南 郑州450001)
具有等待时间的复杂可修复系统的指数稳定性
陆世炎1,李全艳2,金光植1*
(1.延边大学理学院 数学系,吉林 延吉133002;2.郑州大学 数学系,河南 郑州450001)
研究了具有等待时间的复杂可修复系统的指数稳定性.利用泛函分析的方法将模型方程组转化成抽象的Cauchy问题,运用强连续算子半群理论证明了系统动态非负解的指数稳定性.
C0-半群;拟紧性;可修复系统;指数稳定性
文献[1]的作者建立了具有等待时间的复杂可修复系统模型,并用Laplace变换研究了系统的各项可靠性指标,得到了Laplace变换下的状态概率.在文献[2-3]中作者分别运用积分方程理论证明了此类模型动态非负解是存在唯一的.在文献[4]中赵占峰等运用泛函分析的方法,将问题转化成了抽象的Cauchy问题,并运用强连续算子半群理论证明了该系统动态非负解的适定性.本文将延续和推广文献[4]的结论,即证明该系统动态解的指数稳定性.
1 系统假设与预备知识
首先对系统做如下假设:①最初,机器处于完好状态;②机器有2个状态,即好与故障;③机器有n个部件;④机器修复如新;⑤在修复的系统中只要有一个因素改变就可以使系统的状态在任何瞬间发生改变;⑥机器只有在状态6(state 6:machine failed and awaitingrepair.详情见文献[1])的情况下才能被修理;⑦机器的各个组成部分的故障率和修复率是常数;⑧故障类型(硬件、人和系统故障)可能发生在机器的操作阶段;⑨等待率是常数.记λH1表示当机器因为安全失灵无法工作时硬件的故障率;λH2表示当机器因为故障无法工作时硬件的硬件故障率;λh1表示当机器因为安全失灵无法工作时人为的故障率;λh2表示当机器因为故障无法工作时人为的故障率;ωi表示部件从状态i到6的等待率(i=1,2,3,4);ω5表示部件k(k=1,2,…n)从状态5到6的等待率;λ表示部件k(k=1,2,…n)从状态5到6的故障率;μ(x)表示风险函数;pi(t)表示在时刻t系统处于状态i的概率(i=0,1,2,3,4,5);p6(x,t)表示在时刻t系统处于状态6,并且已经用的修复时间是x的概率密度函数.文献[1]的系统模型可由积分 微分方程组表示如下:
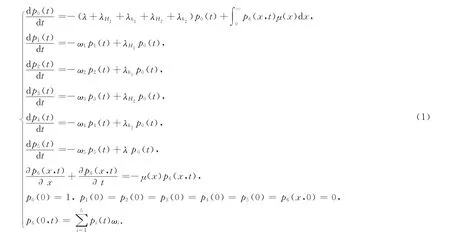
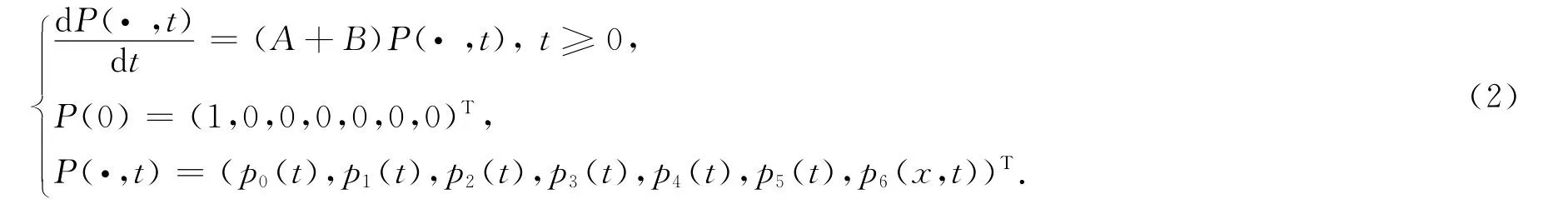
根据实际情况可假设维修率的均值存在且不恒等于零[5-6].
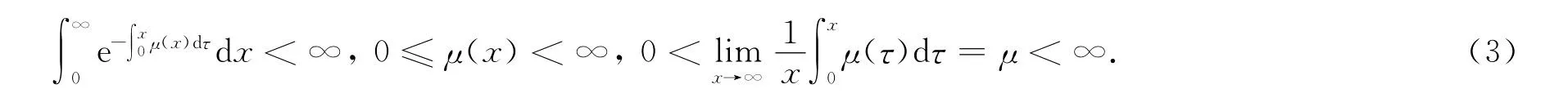
2 主要结果
为了证明系统解的指数稳定性,先假设λ1=λH1,λ2=λh1,λ3=λH2,λ4=λh2,λ5=λ,并给出以下几个引理.
引理1[4]设算子为如上定义,则可得出以下3个结论:① 当γ>0时,γ∈ρ(A),并且在X中稠密;③T(t)为一正定压缩C0半群.
引理2
证明 对任意γ∈C,Reγ>0或γ=ia(a∈R,a≠0),考虑预解方程(γI-A-B)P=Y,Y∈X,有


解方程(6)得
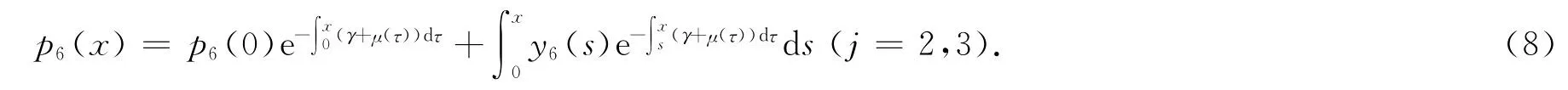
因为y6(x)∈L[0,∞)1,于是有故p6(x)∈L[0,∞)1.将(8)式代入(4)式并联立(5)式得到1个方程组,记其系数矩阵为D(γ),则

定理1 系统(2)具有唯一非负时间依赖解P(x,t),满足:P(·,t)=T(t)P(0)且t∈ [0,∞).
证明 非负时间依赖解P(·,t)可以表示成P(·,t)=T(t)P(0),(P(0)= (1,0,0,0,0,0,0)).由引理知另一方面,因为P(·,t)∈D(A+B)且P(·,t)满足方程组(1),故有因此
定理2 0是算子A+B的简单本征值.
证明 考虑方程(γ-A-B)P=0,取其系数行列式为
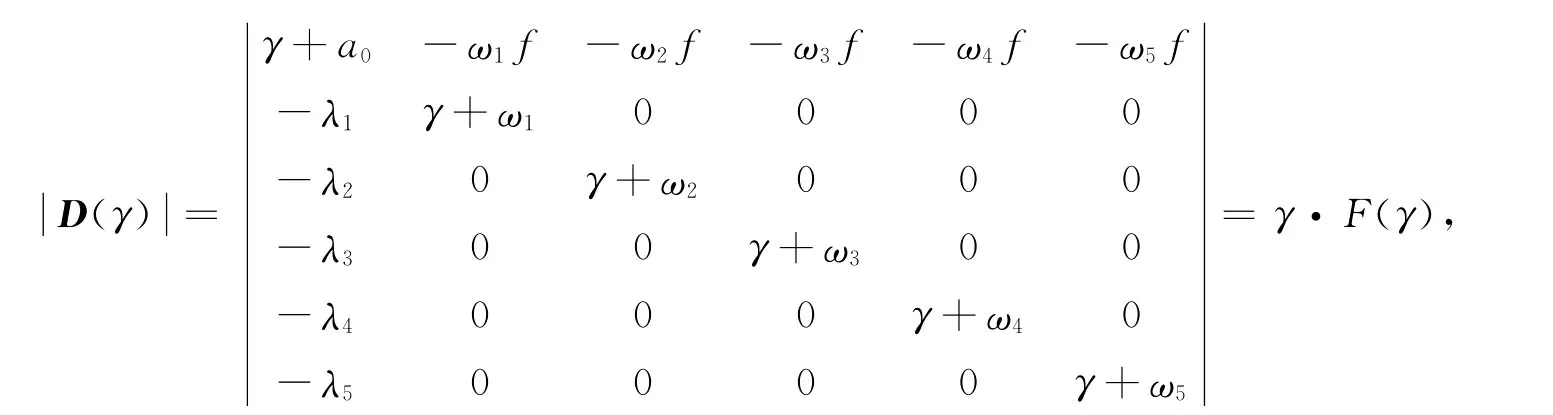
证明 同样考虑方程(γI-A-B)P=Y,类似引理2中的做法,得出D(γ).不难得出是解析函数.此外,当时,故存在N>0,c>0,使得时,因此,当-μ<Reγ≤0时,有至多可数个重数有限的零点,且均含在区域中.由此易知这些零点均为代数重数有限的本征值,并且这些零点的几何重数有限,故代数重数有限,定理得证.
以上定理中零点不属于算子A+B的本质谱为σess(A+B),于是-μ},最后根据etσess⊆σess(T(t))可得出Wess(A+B)≥-μ.我们先考虑以下算子A生成的半群S
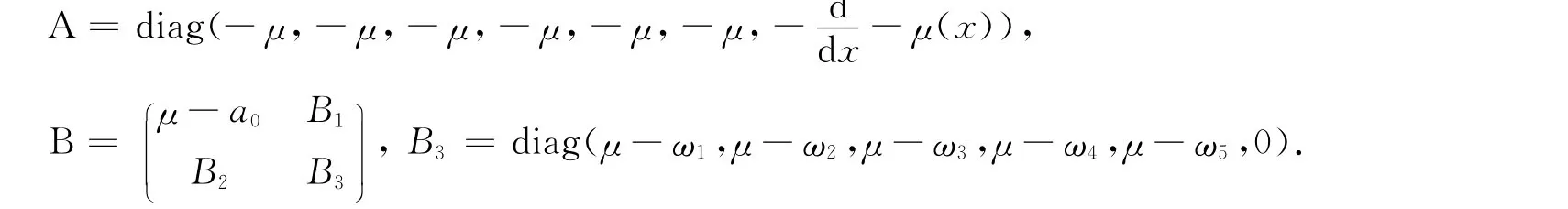
显然,算子B为紧算子,对任意P∈D(A),有

易证算子A生成的C0-半群S(t)对任意φ∈X满足

定理4 系统算子A+B生成的C0-半群T(t)是拟紧半群.
证明 以下证明A的本质增长阶Wess(A)<-μ.对于φ∈X,由假设条件(3)并结合(9)式可得,所以因为B为紧算子,于是得到Wess(A+B)=Wess(A)=W(A)=-μ.因此,由文献[8]中性质2.8知,系统算子生成的C0-半群T(t)是拟紧半群.
性质1[8]系统算子A+B生成的C0-半群T(t)可以分解为T(t)=+R(t),其中¯P0是本征值0对应的留数,且 ∃C,ε>0,使得R(t)≤Ce-εt成立.
定理5 系统(2)的非负时间依赖解以指数形式收敛于稳态解,即

证明 由定理1,系统(2)的非负时间依赖解可以表示为P(t)=T(t)P(0),t∈ [0,∞),所以于是得到
[1]Gupta P P,Arvind Kumar.Reliability and MTTF Evaluation of Repairable Complex System under Waiting[J].Microeletron Reliab,1987,27(3):429-432.
[2]郭卫华.一个可靠机器,一个不可靠机器和一个缓冲库构成的系统的定性分析[J].数学实践与认识,2002,32(6):939-943.
[3]郭卫华.一类两个相同部件并联可修复系统解的存在性和唯一性[J].数学实践与认识,2002,32(4):632-634.
[4]赵占峰,王鸿燕,亓正申.具有等待时间的复杂可修复系统解存在的唯一性[J].平顶山学院学报,2009,24(5):78-81.
[5]Hu W W,She Z F,Xin Y H,et al.Exponential Stability of a Repairable System with Imperfect Switching Mechanism[J].Asymptotic Analysis,2007,54(1):93-102.
[6]Hu W W,Xu H B,Yu J Y,et al.Exponential Stability of a Reparable Multi-state Device[J].Journal of Systems Science and Complexity,2007,20(3):437-443.
[7]程云鹏.矩阵论[M].西安:西北工业大学出版社,2002.
[8]Arendt W,Nagel.One-parameter Semigroups of Positive Operators[M].Ne wYork:Springer-Verlag,1986.
[9]Pazy A.Semigroup of Linear Operators and Applications to Partial Diffierential Equations[M].Ne wYork Springer,1983.
Exponential Stability of a Repairable Complex System under Waiting
LU Shi-yan1,LI Quan-yan2,JIN Guang-zhi1*
(1.DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,China;2.DepartmentofMathematics,ZhengzhouUniversity,Zhengzhou450001,China)
This paper studied the exponential stability of a repairable complex system under waiting.We transfered equations of the model into an abstract Cauchy problem using the method of the functional analysis.Applying the theory of strong continuous semi-group,we proved the exponential stability of the dynamic nonnegative solution of the system.
C0-semigroup;quasi-compactness;repairable system;exponential stability
O177
A
1004-4353(2011)03-0226-04
2011 -06 -11
*通信作者:金光植(1959—),男,副教授,研究方向为统计学.
