一类广义的MKZ算子的点态逼近估计
2011-01-15连博勇
连博勇
(仰恩大学 数学系,福建 泉州362014)
一类广义的MKZ算子的点态逼近估计
连博勇
(仰恩大学 数学系,福建 泉州362014)
利用经典的Zeng分解方法,并结合 Meyer-König和Zeller算子基函数的界,讨论了 Meyer-König和Zeller-Bézier算子在0<α<1时对一般有界函数的逼近,拓展了文献[1-2]的研究结果.
Meyer-König和Zeller-Bézier算子;逼近度;一般有界函数
0 引言
对于定义在区间[0,1]的函数f,Meyer-König和Zeller算子定义为


文献[1-2]给出了算子Mn,α(f,x)在α≥1和0<α<1时的逼近性质.关于~Mn,α(f,x)的一些逼近性质,可以参考文献[3-5].本文研究了~Mn,α(f,x)在0<α<1对一般有界函数的逼近,并得到了比较精确的收敛阶.首先给出一些基本记号及定义.
定义1 设f是定义在区间[0,1]上的函数,
1 主要结果
定理1 设f是定义在区间[0,1]上的有界函数,0<α<1,并且 ∀x∈ (0,1),f(x+),f(x-)存在,则当n足够大时,有其 中gx(t) =为了证明定理1,首先给出一些引理.
引理1[6]设k∈N,x∈ (0,1],有

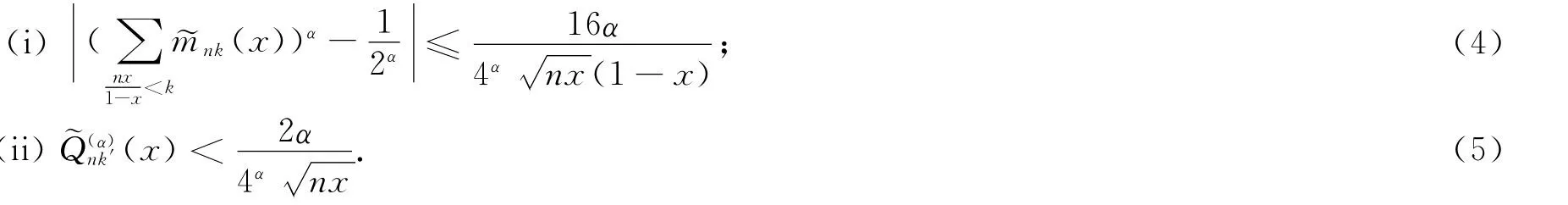
证明 (i)由中值定理得到
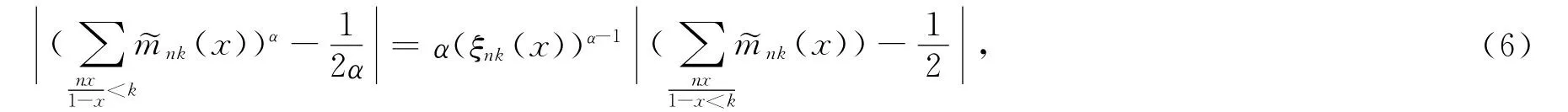
其中ξnk(x)介于和由文献[1]的引理4得

而
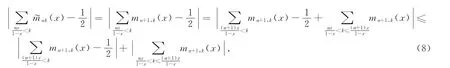
由式(3)得
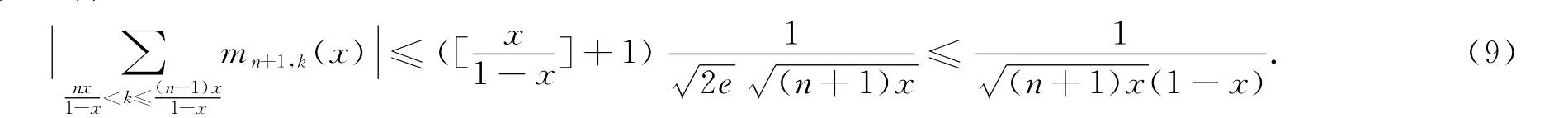
由式(7)、(8)、(9),并且经过简单的计算得

类似于文献[2]的证明,我们可以得到引理3.
引理3 (i)对所有的0<α<1和0≤t<x<1,我们有(ii)对所有的0<α<1和0≤x<t<1,我们有
定理1的证明 由定理1的条件,f(t)可以分解成4个部分之和其中因此,
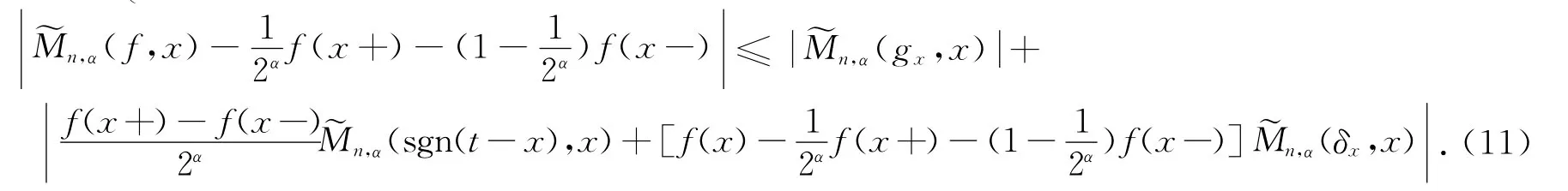
通过直接的计算,易得

而
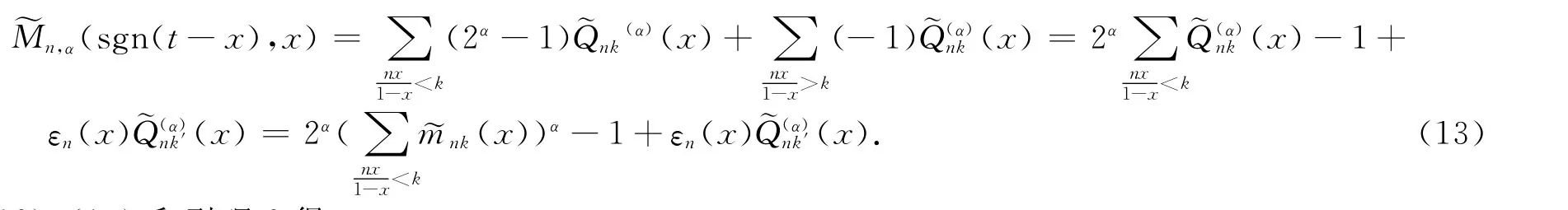
由式(12)、(13)和引理2得
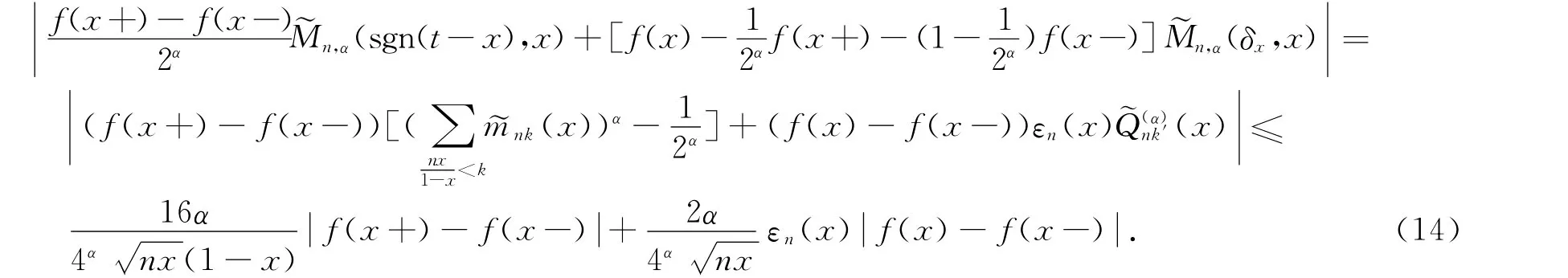
由文献[2]的证明方法,容易得到

联合(11)、(14)、(15)式,定理1得证.
[1]Zeng X M.Rates of Approximation of Bounded Variation Functions by Two Generalized Meyer-König-Zeller Type Operators[J].Comput Math Appl,2000,39:1-13.
[2]Zeng X M,Lian B Y.An Estimate on the Convergence of MKZ-Bézier Operators[J].Comput Math Appl,2008,56:3023-3028.
[3]Abel U.The Moments for the Meyer-König-Zeller Operators[J].J Approx Theory,1995,82:352-361.
[4]Abel U.The Complete Asymptotic Expansion for the Meyer-König-Zeller Operators[J].J Math Anal Appl,1997,208:109-119.
[5]Guo S,Qi Q.The Moments for the Meyer-König and Zeller Operators[J].Appl Math Lett,2007,20,719-722.
[6]Zeng X M.Bounds for Bernstein Basis Functions and Meyer-König-Zeller Basis Functions[J].J Math Anal Appl,1998,219:364-376.
An Estimate on the Convergence of the Generalized Meyer-König and Zeller Operators
LIAN Bo-yong
(DepartmentofMathematics,Yang-enUniversity,Quanzhou362014,China)
By means of the decomposition technique of Zeng,together with the exact bound of Meyer-König and Zeller operator basis functions,we studied the rate of Meyer-König and Zeller-Bézier operators for bounded functions in the case 0<α<1.The results extend the references of[1]and[2].
Meyer-König and Zeller-Bézier operator;rate of convergence;bounded functions
O174.41
A
1004-4353(2011)03-0220-03
2011 -07 -22
连博勇(1982—),男,讲师,研究方向为函数逼近论.
