ARIMA（p，d，q）利息力模型下生存年金精算现值的研究

洪义成，姜今锡，金光植

（1.延边大学理学院 数学系，吉林 延吉133002；2.延世大学理学院 数学系，首尔120－749）

ARIMA（p，d，q）利息力模型下生存年金精算现值的研究

洪义成1，2，姜今锡1，金光植1

（1.延边大学理学院 数学系，吉林 延吉133002；2.延世大学理学院 数学系，首尔120－749）

把精算实务中利息力的随机性用ARIMA（p，d，q）随机过程来表示，并利用矩阵代数理论将其转换成较简单的矩阵形式，然后以此为基础探讨了企业生存年金的精算现值问题.

ARIMA（p，d，q）模型；企业生存年金；精算现值

0 引言

企业年金是指企业为其员工提供的养老金，是政府公共养老保障体系的重要补充，其主要目的是为了保障被保险人的生活水平免受退休后收入下降的影响.影响企业年金定价的因素有两种：一是被保险人群的死亡率，另一个是利率.其中利率给企业年金的定价所带来的影响大于死亡率的影响，而且保险精算中的若干重大问题，如准备金的提留、保费的定价问题等都与利率有关.企业年金中的利率会给企业投资收益率带来一定的影响，即如果预定利率设定过高，会使企业年金赤字加大，而预定利率设定过低，会使员工得不到应有的保障，因此，研究在随机利率下的企业年金具有重要意义.

目前，生存年金的研究方法主要有时间序列分析法和随机过程方法.早在1971年，J.H.Polland［1］第一次把利息力作为一个随机变量，对精算函数进行了研究.随后，国外的一些学者［2－6］基于可逆的MA（1）模型、MA（2）模型、稳定的AR（2）模型和稳定的AR（p）模型对生存年金或养老金的精算现值进行了研究，但是这些模型由于限制条件或假设过于苛刻，因此很难应用于实践.我国学者［7－11］也分别基于MA（q）模型、广义条件下的AR（p）模型、稳定的AR（p）模型、可逆的MA（q）模型、一般MA（q）模型和条件ARMA（p，q）模型对生存年金进行了相应的研究.本文利用时间序列和矩阵理论方法将企业年金中利率推广成更为一般化的ARIMA（p，d，q）模型，得到随机利率下生存年金精算现值模型，这对于解决企业合理发放养老金，避免出现养老基金赤字问题具有一定的理论指导意义和实际应用价值.

1 利率模型

在传统的精算学理论中，为了计算方便往往会把利率或利息力假定为常数，或者简单地假定为各期之间相互独立的随机变量.但是，由于我国正处于经济转型期，市场利率的变化可能会受到过去几年的投资结构、经济因素和政府政策的影响，因而不能简单地把利率或利息力的变化视为相互独立的随机变量.本文中我们假定各期间的利息力序列｛δt∶t∈T｝遵从较为一般化的ARIMA（p，d，q）过程，即

其中：φi和θj为随机过程的系数（i＝1，2，…，p；j＝1，2，…，q）；特别地，我们假定φ0＝θ0＝－1；｛εt∶t∈T｝是均值为0的正态白噪声序列；B是延迟算子，即对任意的t，p∈Z有xt－p＝Bpxt，且假定各系数满足ARIMA（p，d，q）过程成为稳定、可逆的随机过程.

假定ΔT＝ （δ1，…，δT）T和εT＝ （ε1，…，εT）T均表示T行1列矩阵，Δ＊＝ （δ1－（d＋p），…，δ0）T和ε＊＝ （ε1－q，…，ε0）T分别表示d＋p行1列矩阵和q行1列矩阵，以及

其中k是整数，.特别地，当j＜0或j＞d时，令则可以得到ARIMA（p，d，q）随机过程的矩阵表达式：

2 结论

利用（2）式可方便地讨论当利率或利息力遵从ARIMA（p，d，q）随机过程时，生存年金的相关问题.本文主要对生存年金的精算现值问题进行讨论.

结论1 若利息力序列｛δt∶t∈T｝遵从ARIMA（p，d，q）随机过程，则有

证明 根据（2）式可以得到

又因为Δ＊＝ （δ1－（d＋p），…，δ0）T和ε＊＝ （ε1－（d＋p），…，ε0）T是已知量，且εT＝ （ε1，ε2，…，εT）T～NT（0T，σ2IT），所以有证毕.

结论2 若利息力序列｛δt∶t∈T｝遵从ARIMA（p，d，q）随机过程，则利息力累积函数序列｛R（T）∶t∈T｝遵从均值为其方差为的正态分布，其中

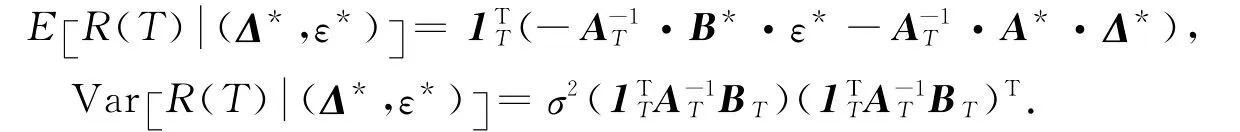
当t≤T时，以下结果仍成立的：

结论3 若利息力序列｛δt∶t∈T｝遵从 ARIMA（p，d，q）随机过程，则折现函数序列｛v（T）∶t∈T｝的均值为

3 ARIMA（p，d，q）利息力模型下的生存年金

设某保险公司推出的某种生存年金规定：当被保险人活过退休年龄r岁时，该保险公司在每个保单年度末对每个参保人给付1单位元的保险金.假定参加此险种的参保人共有N人，且根据参保人的年龄，将所有参保人分成k组，即假定xj岁的参保人共有nj人，显然若以ar表示参保人的生存年金（退休金）在其退休年龄初的现值，则有

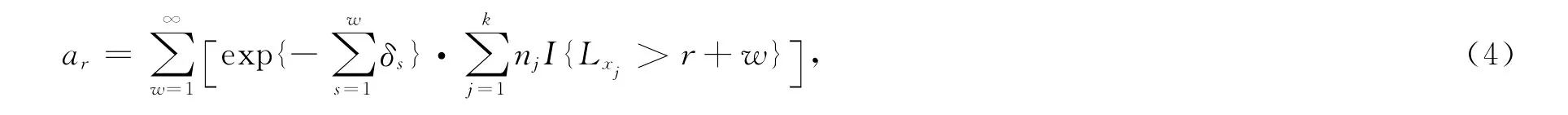
其中I｛·｝是示性函数，Lxj表示xj岁的个体的未来生存时间，δs表示第r＋s个保单年度，即年龄段（r＋s－1，r＋s）期间内的利息力.

证毕.

［1］Polland J H.On Fluctuating interest rates［J］.Bulletin De l’Association Royal des Actuaries Belges，1971，66：68－97.

［2］Bellhouse D R，Panjer H H.Stochastic Modeling of Interest Rates with Applications to Life Contingencies II［J］.Journal of Risk and Insurance，1981，47：628－637.

［3］Frees E W.Stochastic Life Contingencies with Solvency Considerations［J］.Transaction of Societies of Actuaries，1990，42：91－148.

［4］Haberman S.Stochastic Investment Return and Contribution Rate Risk in a Defined Benefit Pension Scheme［J］.Insurance：Mathematics and Economics，1997，19：127－139.

［5］Dhaene J.On Approximating Distribution by Their De Pril transforms［J］.Scandinavian Actuarial Journal，1998，14（1）：1－23.

［6］Perry D E.Long－term Stochastic Interest Rate Models［J］.Insurance：Mathematics and Economics，2001，29：73－82.

［7］高建伟，邱菀华.利率模型为 MA（q）时的生存年金精算现值模型［J］.系统工程理论与实践，2002（11）：104－133.

［8］高建伟，李春杰.随机利率下缴费预定型企业年金保险中生存年金精算现值模型［J］.系统工程，2004，22（5）：53－56.

［9］高建伟，丁克诠.基于MA（q）利息力下交费预定性企业年金保险中生存年金精算现值模型［J］.系统工程，2004，22（11）：74－78.

［10］高建伟，张兴平，高明.缴费预定型企业年金保险中基于滑动平均利率的生存年金精算现值模型［J］.系统工程理论与实践，2006（8）：27－32.

［11］解强，李秀芳.基于 ARMA（p，q）利息力生存年金精算现值模型［J］.数学的实践与认识，2009，39（3）：74－79.

The Life Annuity Actuarial Present Value Models Based on ARIMA（p，d，q）Force of Interest Rate

HONG Yi－cheng1，2，JIANG Jin－xi1，JIN Guang－zhi1
（1.DepartmentofMathematics，CollegeofScience，YanbianUniversity，Yanji133002，China；2.DepartmentofMathematics，SchoolofScience，YonseiUniversity，Seoul120－749，Korea）

We assumed that interest rate follows an ARIMA（p，d，q）process and transformed it into more simple matrix form using matrix algebra theory，and then discussed actuarial present value of annuity.

ARIMA（p，d，q）model；enterprise life annuity；actuarial present value

O211.9；F840.67

A

1004－4353（2011）03－0216－04

2011 -03 -17

洪义成（1980—），男，讲师，研究方向为应用概率统计和精算实务分析.

吉林省教育厅“十一五”科学技术研究资助项目（吉教科合字［2007］第自11号）