不等长双缝夫琅禾费衍射光强分布
2011-01-12史勤益梁华秋
史勤益,梁华秋
(台州学院 物理与电子工程学院,浙江 台州 318000)
不等长双缝夫琅禾费衍射光强分布
史勤益,梁华秋
(台州学院 物理与电子工程学院,浙江 台州 318000)
根据夫琅禾费衍射与傅立叶变换的关系,数值计算了由宽度相同而长度不同双缝组成衍射平面的夫琅禾费衍射光强分布,结果表明双缝长度之比是影响干涉条纹的可见度的主要因素。
夫琅禾费衍射;不等长双缝;傅立叶变换;光强分布
1 引言
衍射是光波动性的表现之一。双缝衍射本质上是单缝衍射与双缝干涉共同作用的结果,在光学教学中分析不同情况下双缝衍射的条纹特征,可以加深对光波干涉与衍射的理解。对衍射光强分布的计算一般采用惠更斯-菲涅耳原理,由于计算复杂,普通教材中只对等长等宽双缝的衍射光强分布给出解析解[1,2]。如果狭缝的长度或宽度不同,对衍射光强分布又会产生怎样的影响呢?我们注意到洪正平等[3]讨论了不等缝宽双缝衍射光强分布特征,张永炬等[4]用光电传感器观测了双缝部分相干干涉光强分布,并对部分相干现象作出理论解释,但至今尚未见到对不等长双缝衍射光强分布进行分析的报导。本文根据夫琅禾费衍射与傅立叶变换的关系,利用数值计算分析不等长双缝的夫琅禾费衍射光强分布特点,并定性分析两缝长度之比对光强分布的影响。
2 计算方法
如图1(a)所示,衍射平面x0y0由宽度相同而不长度不同的双缝组成。狭缝内复振幅透过率为1,狭缝外复振幅透过率为0。两条狭缝缝宽均为b,第一条狭缝长度为l1,第二条狭缝长度为l2,两缝中心之间的距离为d。
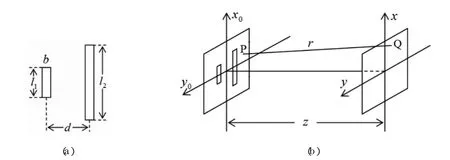
图1 等宽不等长双缝衍射装置,其中(a)不等长双缝衍;(b)衍射平面与观察平面的相对位置
图1(b)表示衍射平面与观察平面的相对位置。衍射平面x0y0与观察平面xy距离为z,衍射平面上点 P(x0y0)与观察平面上 Q(xy)点的光矢量的复振幅分别为 U0(P)、U(Q)。对于夫琅禾费衍射,傍轴条件与远场条件同时得到满足,则有[5]:

上式中 F{U0(x0,y0)}表示 U0(x0,y0)的傅里叶变换。根据光强 I与|U(x,y)|2的正比关系即可求得观察平面上的光强分布。
3 数值计算及结果分析
根据(1)式,对双缝夫琅禾费衍射的光强分布进行数值计算,我们令两缝之间的距离为8b。图3(a)为等长等宽双缝衍射光强分布,图 3(b)~图 3(f)分别显示了两度缝长度之比 l1/l2分别为 1/2、1/4、1/8、1/16、1/32作为衍射平面的夫琅禾费衍射在垂直狭缝方向的光强分布,图3(g)为单缝衍射光强分布。


图2 不等长双缝夫琅禾费衍射在垂直狭缝方向的光强分布
下面我们将分析不等长双缝夫琅禾费衍射在垂直狭缝方向的光强分布特征,定性讨论两条狭缝长度之比对条纹可见度的影响。条纹可见度表示为[6]

从上式可以看出条纹中的光强极小值Imin越大,则可见度越小。从图2中可以看出:
(1)对比图(a)~(f)可以看出,与等宽等长双缝一样,不等长双缝衍射也是单缝衍射与双缝干涉共同作用的结果。双缝干涉形成密集等间距条纹,而每一干涉条纹的光强最大值受单缝衍射的调制。由于我们数值计算时采用d=8b,在不等长双缝衍射图样中,同样可以看到缺级现象,即干涉条纹的缺级发生在第8,16,…,级。
(2)当两缝长度相同,即为等宽等长双缝的衍射,如图2(a)所示,干涉条纹的光强的最小值为0,可见度最大;从图(b)~(f)可以看出,当两缝长度不相同时,干涉条纹的光强的最小值一般不为0,当两缝长度之比l1/l2减小时,也就是说两狭缝长度的相差变大,干涉条纹可见度呈下降趋势;与等长等宽双缝衍射光强分布相比较,当l1/l2分别为1/2、1/4时,虽然条纹可见度变小,但衍射中央主极大所包含的干涉条纹仍然明显可见,当l1/l2降低到1/8时,从图中可知,中央主极大所包含的最旁边的条纹已经消失,当l1/l2继续降低时,就有更多的条纹消失,如当l1/l2=1/32,衍射中央主极大下最多只能观察到0,±1,±2等5条干涉条纹,但可见度较小。
(3)在相同的情况下,单缝衍射除中央主极大以外其余各级所包含的干涉条纹可见度更小,如当l1/l2=1/32时,单缝衍射除中央主极大以外其余各级单缝次极大所包含的干涉光强虽有起伏,但基本上已经不能形成条纹,衍射光强分布与图2(g)所示的单缝衍射光强分布接近。
4 结论
本文根据夫琅禾费衍射与傅立叶变换的关系,计算了宽度相同而长度不同的双缝夫琅禾费衍射光强分布,并分析了衍射光强的分布特点,通过以上分析,可以得出如下结论:
(1)宽度相同而长度不同的双缝的夫琅禾费衍射光强分布,可以看成是单缝衍射与不等长双缝干涉共同作用的结果。缺级的条件及位置与等宽等长双缝相同。
(2)双缝长度之比是影响干涉条纹的可见度的主要因素。当双缝长度差别较大时,在观察平面上将得到的是相当于两列强度相差较大的相干光叠加而形成的图样,干涉条纹的可见度较低。当双缝长度接近时,条纹的可见度较大。当两缝长度相同时,在观察平面上将得到的是普通双缝的夫琅禾费衍射图样,条纹可分见度最大,形成了清晰可见的明暗相间条纹。
在教学中,如果利用激光直接照射双缝观察双缝衍射光强分布,应当尽量使得激光光斑位于双缝中心,如果激光光斑偏离其中心,观察到的相当于不等长双缝衍射的光强分布,将会影响干涉条纹的可见度。
[1]母国光,战元令.光学[M].人民教育出版社,1978:325-331.
[2]姚启钧.光学教程[M].高等教育出版社,2008:96-97.
[3]洪正平,王秀娥,高嵩.不同缝宽双缝衍射光强分布的分析[J].山东师范大学学报(自然科学版),2010,25(3):64-66.
[4]张永炬,冯尚申,梁华秋,郑薇薇.双缝部分相干干涉光强分布观测与分析[J].大学物理,2003,22(4):32-34.
[5]苏显渝,李继陶.信息光学[M].北京:科学出版社,1999:34-47.
[6]E.赫克特,A.赞斯著,詹达三,秦克诚,林福成译.光学(下册)[M].高等教育出版社,1980:867-876.
Fraunhofer Diffraction Light Intensity Distribution of the Double-slit with Inequality Length
SHI Qin-yi,LIANG Hua-qiu
(School of Physics and Electronics Engineering,Taizhou University,Taizhou 318000,China)
According to the relationship between Fraunhofer diffraction and Fourier transformation, the Fraunhofer diffraction light intensity distribution of the double-slit with equality wideth but inequality length is numeriacally calculated. The result shows that the proportion of the length of the double-slit will mainly affect the visibility of the interference fringe of the double-slit.
Fraunhofer diffraction;double-slit with inequality length;Fourier transformation;light intensity distribution
周小莉)
R730.2
A
1672-3708(2011)06-0017-04
2011-08-23;
2011-08-28
梁华秋(1 9 6 7- ),男,浙江临海人,副教授,主要从事量子信息研究及光学教学研究。
