“单摆测重力加速度”的实验研究与误差分析

王金德

（ 沧州师范学院 物理与电子信息系，河北 沧州 061001 ）

“单摆测重力加速度”的实验研究与误差分析

王金德

（ 沧州师范学院 物理与电子信息系，河北 沧州 061001 ）

以“单摆测重力加速度”的力学实验为例，从误差理论出发，讨论怎样减小测量误差以及对单摆测重力加速度实验的最优化设计。

单摆实验； 重力加速度； 误差分析； 实验设计

科学地设计实验方案、合理地选择实验仪器、运用误差理论寻求减小误差的方法，做出令人满意的实验结果，是物理教师应具备的基本实验素质，能有效地指导学生设计实验，提高学生的实验能力，培养科学探究精神。科学的实验设计方法，要求物理教师在一定实验条件下，从实验的误差分析入手，寻找误差的主要来源，运用误差理论，提出减小误差的问题，提高实验精度的手段、方法和措施。遵循的原则是：“力求用最小的代价，来获取最佳的效果，不能一味地追求仪器越高级越精密越好，环境越稳定越好，测量次数越多越好，方法越完善越好”。本文以“单摆测量重力加速度”为例，说明如何设计实验和减小误差。

1.通过系统误差分析设计较为理想的单摆

把一个质点，用一根不可伸长的几何线段悬于一点，即构成理想的单摆，其运动方程是：

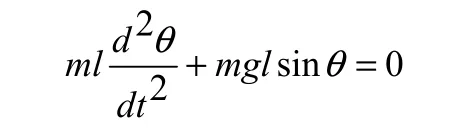
在摆角很小的情况下其做简谐振动，近似解为：

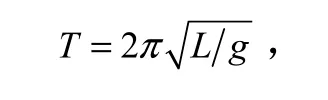
在实际实验中，质点用一摆球，悬线用一根“细”“刚”线，尽管在制作中，使摆球尽量小、尽量接近质点，悬线尽量细轻，其质量近于忽略，受力变化引起的摆长变化也忽略，但上述原因毕竟不能实现理想的数学摆模型。加之空气浮力和空气阻尼等诸多因素，都会对实验结果带来系统误差。

1.1. 摆球半径和悬线质量的影响

设L为悬点到摆球质心的距离，r为摆球半径，m为摆球质量，为悬线质量，在要求较高的单摆实验中，应做复摆修正，其运动方程则变为：

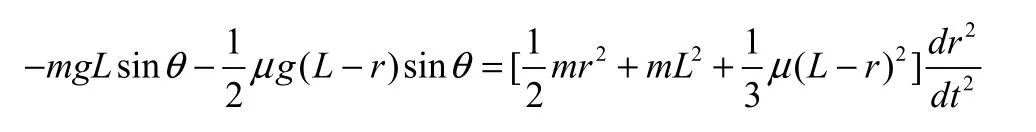
在摆角很小的情况下的近似解为：由（1）式，悬线质量的影响使重力加速度测量值偏小。对摆球半径的影响，可令μ=0进行修正

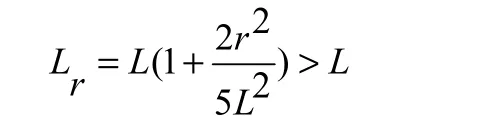
重力加速度的测量值偏大。

1.2. 摆角影响

摆角很小的条件亦难以满足，若取二级近似，有

可得θ＜5.1°，一般可取θ＜5°。

1.3. 实验操作对测量准确性的影响

实验时许多学生不是由最高点释放，而是要“送上一程”，给小球一个速度，若其速度方向和重力方向不共面，则单摆会变椭圆锥摆，其影响可联系圆锥摆的周期公式：

两者进行比较，带来系统误差使得重力加速度的测量值偏大。实验采用累积计时办法，因同一实验者的固定习惯，对计时亦带来系统误差，针对这种情况，可采用类似“导号”的办法，在不改变摆长情况下，让不同习惯的实验者进行测量，求出周期的平均值，可减小该原因带来的系统误差。

摆球摆动中摆球在不同位置，其速度大小是不同的，过平衡位置时速度最大。对同一实验者，如果空间定位的误差不变，摆球速度越大，计时误差越小，周期测量也就越准确所以实验应从平衡位置开始计时。实验中，不少实验者视线与摆平面不垂直，这对测量结果亦会带来系统误差，但只要保持视线方向不改变，在不计入半个周期的情况下，本误差会自动消除。所以要求在实验计时时，保持相对稳定的视线方向。若停表不准，会对实验结果带来系统误差。这需在实验前对停表进行校准，方法是选择一个数字毫秒表作为标准表，如停表在走过tn秒的时间时，毫秒表走过了ts秒，则校准系数为C=ts/tn，将实验测出周期T'乘以校准系数C即T=CT'才是真正测出的周期。

1.4. 其他因素的影响

实际摆动中受到空气浮力的作用，在摆球密度不是很大时，应做浮力修正，实际测量加速度应为重力和浮力的合力产生加速度，将它作为重力加速度，测量值偏小。

实验中还应考虑空气阻尼带来影响。可以分析它使得周期偏大，重力加速度偏小。但因为摆长较长，速度不大，阻力很小，所以影响很小。

2.从误差分析，寻找测量误差的主要来源

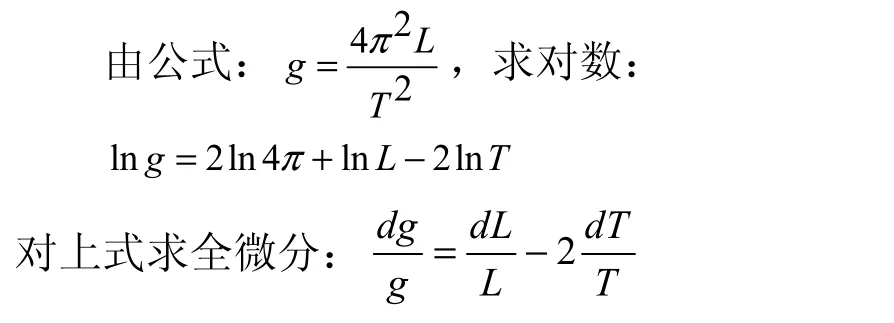
在进行随机误差分析中，需将“—”号变成“+”号，同时将“d”变为“Δ”，有：从上式可看出重力加速度测量的误差来源于摆长的周期测量。

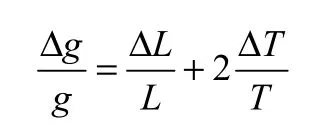
实验中若采用长度约为 1米的细线，摆球用直径约为2cm的小球，用mm刻度尺测得摆线长度按1m计算，用卡尺测得摆球直径按2cm计算，有摆长L=（101.00±0.05）cm，周期测量若选用实验室常用精密度为（1/10）s的停表进行直接测量，测量结果按2.1s计算，有T=（2.1±0.1）s，由间接测量的误差传递公式（4）：

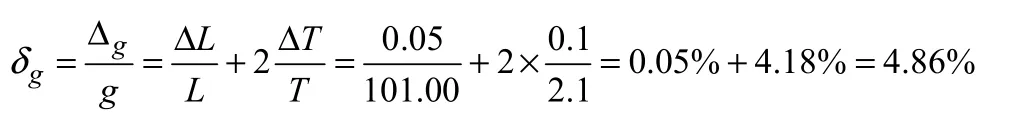
从上述结果不难看出，实验误差主要来源于周期T的测量。

3.实际设计方案的制定

厘米刻度尺和（1/10）s的停表均为实验室常用仪器，但带来的误差相关悬殊。从实验设计角度上讲，摆长和周期测量的误差不能采用均分的办法，更没有必要过分追求刻度尺的精密度（用卡尺测摆球直径，其目的是方便测量，而不提高精密度），实际设计的着重点放在减少周期测量的误差上，而减少这个误差又绝不能靠提高停表的精密度。这是因为计时时，定位的计时误差较大，即使“准确度”最高的人，其定位的计时误差也远远大于停表的精密度。怎么办呢？有效的办法是采用累积计时的方法。

还以上面数据为例，为使重力加速度测量误差不超过2%，应如何制定实际方案呢？由误差公式：

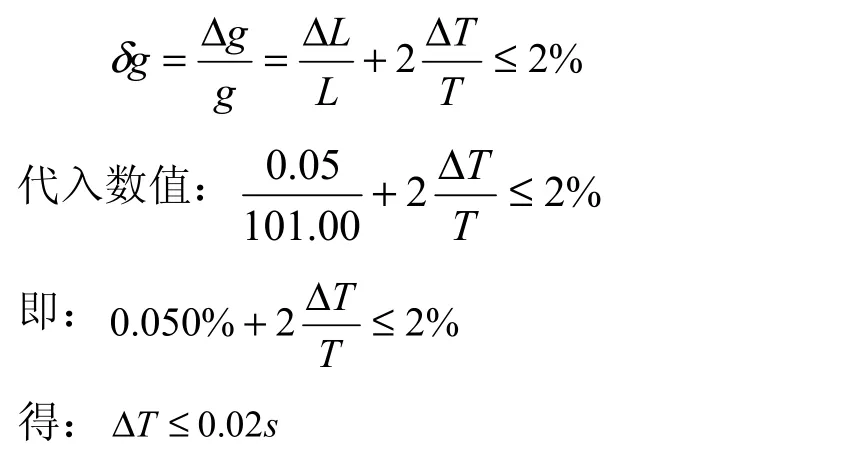
（1）从单纯的仪器选择角度，选用实验室常用的停表，其精密度若为（1/10）s，进行累积计时，如测出n=10次全振动所用时间T=（21.0±0.1）s，周期T=t/ n=（21.0±0.1）s ，ΔT=0.1s/10=0.01s＜0.02s就可满足要求。

可求得，n′≥26.25。所以在实验中，一般测量连续摆动30个全振动所用时间来计算周期T。

用单摆测重力加速度，在理论上分析上述原因对实验都带来系统误差的基础上，将单摆模型理想化，不要求学生一定分析上述原因带来的是何种影响的结论，引导学生进行科学探究。但为了减小这些影响，教师在制作单摆时，对摆线的要求是轻、细、软，以使其质量和伸缩忽略不计，且要求合适的长度（不小于1米）；摆球应选用密度较大的材料（铜、铁），制成半径远小于摆长有中心孔的实心小球。安装时应使摆的悬点位置固定不变，摆动时摆角应小于5°，这些即可保证实验的单摆尽可能接近理想的单摆。

由于普通物理实验室单摆仪器设备较为简单，我们要学会一套实验设计方法，用误差理论引导学生做出令人满意的实验结果来，这是物理教师应具备的一项基本教学素质。

[1] 曾贻伟等.普通物理实验教程[M].北京：北京师范大学出版社，1989.

Experimental Study and Error Analysis in the experiment of “measuring acceleration of gravity by single pendulum”

WANG Jin-de
（ Department of Physics and Electronic Information, Cangzhou Normal University, Cangzhou, Hebei 061001, China ）

Taking the mechanical experiment of “measuring acceleration of gravity by single pendulum” as an example, this paper discussed how to reduce the measurement error and optimal design of the experiment.

experiment of “single pendulumtourism”;acceleration of gravity;error analysis;experiment design

（责任编辑 李宗宝）

O3 < class="emphasis_bold">文献标识码：A

A

1673-9639 （2011） 03-0126-03

2011-04-26

王金德（1965-），男，河北沧州人，河北沧州师范学院物理与电子信息系副教授，主要承担物理教学论、多媒体教学技术课程的教学。