高维Möbius群中的Jφrgensen不等式＊

李长军，孔玉瑾

（中国海洋大学数学科学学院，山东青岛266100）

高维Möbius群中的Jφrgensen不等式＊

李长军，孔玉瑾

（中国海洋大学数学科学学院，山东青岛266100）

利用高维Möbius变换群中的Clifford矩阵表示，在二元生成群中当f是双曲元素或严格抛物元素，且f和g有公共不动点时，对f和g的不动点，f和g的交换子的迹之间的关系进行了研究。得到它们等价的一个充要条件，还得出当f和g的交换子是严格抛物元素时，平面上的Jφrgensen不等式在高维空间上仍成立。

Clifford矩阵；交换子；Jφrgensen不等式；初等群

0 引 言

自1976年Jφrgensen提出判定Möbius变换群离散性的“Jφrgensen不等式”，许多数学工作者都在从事研究与“Jφrgensen不等式”相关的Möbius变换群不等式，并且取得较好的结果。特别是1985年，数学家L．V．Ahlfors的杰出工作［1－2］，使高维Möbius变换群和高维Jφrgensen不等式的研究成为研究热点。由于高维Jφrgensen不等式的情形比平面情形较为复杂，在这方面的研究较难取得很大的进展。

本文将文献［3］的一个定理推广到高维情形：

设f∈SL（2，H），定义g0＝g∈SL（2，H），gn＋1＝且f不是运动元素或椭圆元素，如果存在n0∈N使得gn0＝f，那么＜f，g＞是初等群。

注：H表示四元数全体，其元素x＝x0＋x1e1＋x2e2＋x3e3，＝－1，e3＝e1e2＝－e2e1）其中xi∈R，i＝0，1，2，3。若x3＝0，则称x为向量，由于全体向量及H都是线性空间，故将全体向量视为R3，H视为R4。

文献［3］中要求f不是运动元素或椭圆元素，本文考虑了f是双曲元素和严格抛物元素时的情形。另外，本文还利用该定理证明了，当f为双曲元素和严格抛物元素时，高维Jφrgensen不等式是存在的。

1 预备知识

Clifford代数An为由1，e1，e2，…，en－1在实数域R上生成的非交换结合代数，其中ej（j＝1，2，…，n－1）满足e2j＝－1，eiej＝－ejei（i≠j），An中任一元素a能唯一地表示成

其中a0，av∈R，∑是对所有的复指标v＝（v1，v2，…，vp）求和，Ev＝ev1ev2…evp（0＜v1＜v2＜…＜vp＜n－1），a0称为a的实部。

称特殊形式的Clifford数x＝x0＋x1e1＋…＋xn－1·en－1为向量，这些向量构成一个n维子空间Vn，常把Vn等同于Rn。

定义1 An中任一元素a，意a＝a0＋∑avEv∈An，有下面3种重要的对合运算：

（ⅰ）′运算a′＝a0＋∑avE′v，其中E′v＝（－ev1）（－ev2）…（－evp）＝（－1）pEv；

（ⅲ）－运算a珔＝（a′）＊＝（a＊）′。

易知，′运算确定了An的一个自同构，而＊运算和－运算确定了An的反自同构，有

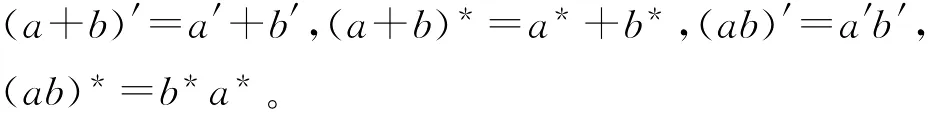
对向量x＝x0＋x1e1＋…＋xn－1en－1≠0，有x＊＝x，

定义2 Clifford群Γn由An中所有可以表示为Rn中有限多个非零向量乘积的元构成。

（ⅰ）a，b，c，d∈Γn∪｛0｝；

（ⅱ）ad＊－bc＊＝1；

（ⅲ）若c≠0，则ac－1∈Rn且c－1d∈Rn；

（ⅳ）若d≠0，则db－1∈Rn且b－1a ∈Rn。

注：条件ac－1∈Rn等价于c＊a＝a＊c，这是因为（c＊′）－1＝｜c｜－2c且c＊a＝a＊（ac－1）c＝｜c｜2c＊（ac－1）（c＊）′－1。类似地，有：

cd＊＝dc＊∈Rn，b＊d＝d＊b∈Rn，ab＊＝ba＊∈Rn。

用SL（2，Γn）表示全体n维Clifford矩阵关于矩阵乘法构成的群，对任意Möbius变换g∈M（Rn），有

对Möbius变换g∈M（Rn）／｛Id｝，有：

定义9 如果g在珚Rn中没有不动点，则称g为运动元素。定义10 设G是M（）的子群，对G中任意序列｛gn｝，若gn→I，则存在N，当n＞N时，gn＝I，那么称G是离散群。

文中采用的记号和术语与文献［2，4－8］相同，例如Möbius变换群M）、离散群等。

采用如下由文献［5］给出的初等群定义：定义11 如果G在H珨n＋1中有一个有限轨道，那么称G是初等的，否则，G是非初等的。定理A［8］Jφrgensen不等式：假设Möbius变换f和g生成一个离散非初等群，则｜tr2（f）－4｜＋｜tr（fgf－1·g－1）－2｜≥1，并且这个下界是最佳的。

2 主要结果及其证明

定理1 设f，g∈SL（2，Γn），若f是双曲元素或严格

证明 当f是双曲元素时，由迹共轭不变性，

Γn），则有

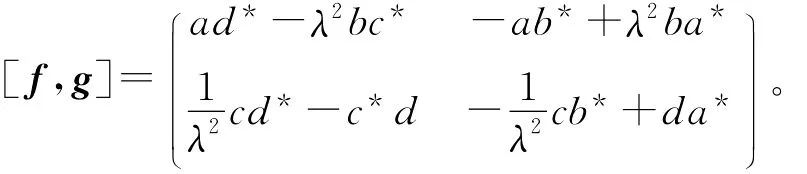
从而可得：

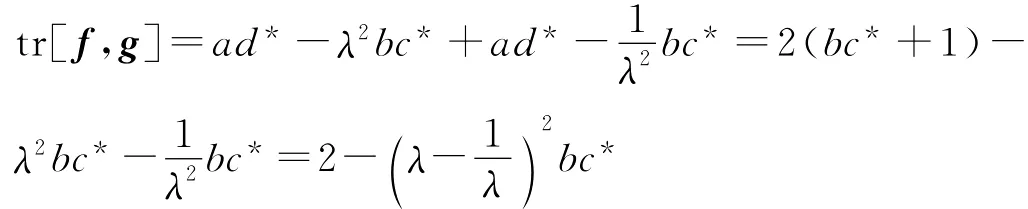
若f和g有一个公共不动点，则b＝0或c＝0，从而tr［f，g］＝2。

反之，若tr［f，g］＝2，则bc＊＝0，从而b＝0或c＝0，即f和g有一个公共不动点。

当f是严格抛物元素时，由迹共轭不变性，可设

从而可得：tr［f，g］＝2＋λ2bb＊。

若f和g有一个公共不动点，则b＝0，从而tr［f，g］＝2。

反之，若tr［f，g］＝2，则tr［f，g］＝2＋λ2bb＊＝2，从而b＝0，即f和g有一个公共不动点。［证毕］

注：当f是椭圆元素时，结论不一定成立。当n＝3时，即在三维空间中，易举出反例。事实上，只要取

易知f和g有一个公共不动点，且

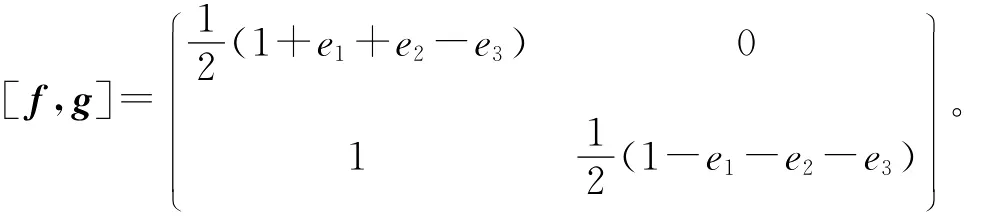
由文献［9］中判别法可知f是椭圆元素。此时，tr［f，g］＝1。

同样，当f是椭圆元素且tr［f，g］＝2时，也不一定能推出f和g一定有公共不动点。

在高维的情形，暂时还未举出反例。

定理2 设f，g∈SL（2，Γn），若f是双曲或者严格抛物元素，［f，g］∈∀），且f和g在中有一个公共不动点，则［f，g］是严格抛物元素。

证明 当f是双曲元素时，由定理1得：

由于f和g有一个公共不动点，不妨设b＝0，则

类似地，可证明f是严格抛物元素时的情形。［证毕］

推论3 设f，g∈SL（2，Γn），若f是双曲元素，且f和g在中有一个公共不动点，则或有［f，g］＝I且Ff＝Fg，或有［f，g］是严格抛物元素且Ff≠Fg。证明 由于f是双曲元素，由定理1得：

由于f和g有一个公共不动点，不妨设b＝0，则有

当c＝0时，即g也为双曲元素时，［f，g］＝I且Ff＝Fg。

当c≠0时，［f，g］是严格抛物元素且Ff≠Fg。［证毕］定理4 设f∈SL（2，Γn），定义g0＝g∈SL（2，Γn），且f是双曲元素或严格抛物元素，如果存在n0∈N，使得＝f，那么＜f，g＞是初等群。

（2）当f是双曲元素时，因为gi（i＝1，2，…）与f共轭，所以gi（i＝1，2，…）也是双曲元素。不失一般性，不妨设f的不动点为0和∞。因为＝f，所以0和∞是的不动点。

假设gi＋1（i≥0）以0和∞为不动点，即gi＋1（0）＝0，gi＋1（∞）＝∞，从而可得：

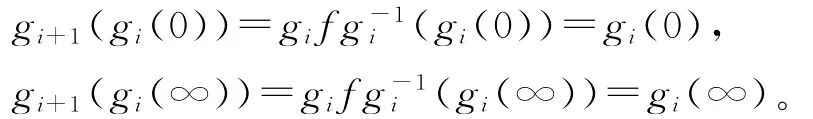
因此｛gi（0），gi（∞）｝＝｛0，∞｝。

假设gi（0）＝∞，gi（∞）＝0。除此之外，gi有2个不动点α，β≠0，∞，则也以α，β为不动点。又因为（∞）＝gigi（∞）＝gi（0）＝∞，（0）＝gigi（0）＝gi（∞）＝0，所以也以0和∞为不动点。从而可得为椭圆元素或单位元素，与gi与（m≥1）同时为双曲元素矛盾。所以gi（0）＝0，gi（∞）＝∞。因而证明了当gi＋1（i≥0）以0和∞为不动点时，gi（i＝1，2，…）亦然。由归纳法可知gi＋1，gi，…，g1，g0均以0和∞为不动点，即gn0，gn0－1，…，g1，g0均以0和∞为不动点。它表明f和g使集合｛0，∞｝保持不变，所以＜f，g＞是初等群。［证毕］

注：该定理将文献［3］中定理2推广到高维空间，只是定理条件有所不同，文献［3］中定理2要求f∈SL（2，H），且f不是运动元素或椭圆元素，该定理仅考虑了f是双曲元素和严格抛物元素时的情形。定理5 设f，g∈M（珚Rn），f是双曲元素或严格抛物元素。若｜tr2（f）－4｜＋｜tr［f，g］－2｜＜1，则＜f，g＞要么初等，要么非离散。证明 当＜f，g＞是初等群时，显然成立。当＜f，g＞是非初等群时，只需证明＜f，g＞是非离散群即可。（1）当f为双曲元素时，

由定理1得：

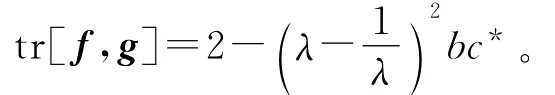
设

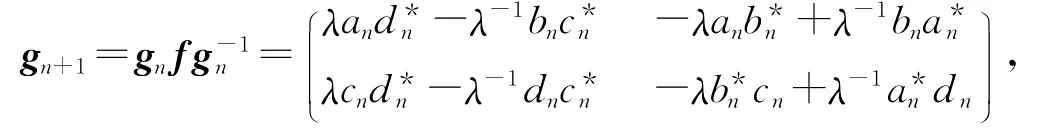
从而可得：

因为＜f，g＞是非初等群，所以bc≠0。

下面用归纳法证明｜bncn｜≤kn｜ad｜，｜bncn｜≤kn｜bc｜。当n＝0时，显然成立，且有：

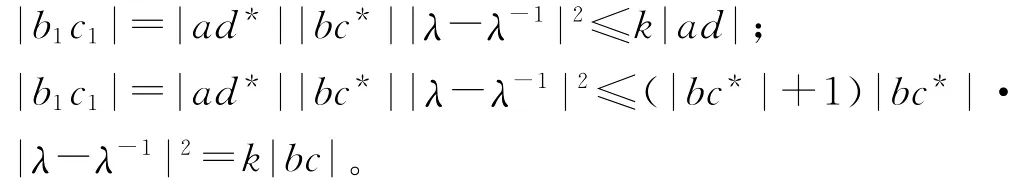
假设n＝m时成立，即｜bmcm｜≤km｜ad｜，｜bmcm｜≤km｜bc｜。

那么当n＝m＋1时，

由数学归纳法可知：｜bncn｜≤kn｜ad｜，｜bncn｜≤kn｜bc｜。

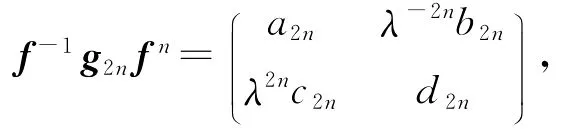
假设＜f，g＞是离散群，则存在m，使得f－2mg2mf2m＝f，即g2m＝f。由定理5可知，＜f，g＞是初等群，与题设矛盾。因此，＜f，g＞是非离散的。

（2）类似地可证明f是严格抛物元素时的情形。［证毕］。

注：该定理是在文献［10］定理2．1的基础上得到的，但是文献［10］的定理2．1要求f和fgfg－1均是双曲元素。该定理只是要求f是双曲元素和严格抛物元素，更具一般性。当f是斜驶元素和椭圆元素时，高维Jφrgensen不等式也是存在的，只是条件有了限制，参见文献［11］。

［1］ Ahlfors L V．Old and new in Möbius groups［J］．Ann Acad Sci Fenn Ser A I Math，1984，9：93－105．

［2］ Ahlfors L V．On the Fixed Points of Möbius Transformations in Rn［J］．Ann Acad Sci Fenn Ser A I Math，1985，10：15－27．

［3］ 乃兵．三维非初等离散Möbius群的必要条件［J］．云南民族学院学报，1994，3（1）：13－19．

［4］ Fang A，Nai B．On the Discreteness and Convergence in n－Dimensional Möbius Groups［J］．J London Math Soc，2000，61（2）：761－773．

［5］ Beardon A F．The Geometry of Discrete Groups［M］．New York，Heidelberg Berlin：Springer Verlag，1983．

［6］ Waterman P L．Möbius Transformations in Several Dimensions［J］．Adv in Math，1993，101：87－113．

［7］ Waterman P L．Purely Elliptic Möbius Groups［A］．Holomorphic Functions and Molulli，II［C］．New York，Berlin：Springer，1988．

［8］ Jφrgensen T．On Discrete Groups of Möbius Transformations［J］．Amer J Math，1976，98（3）：739－749．

［9］ 刘春林．三维Möbius变换的分类及类型判别［J］．数学进展，1990，19（2）：231－238．

［10］ 张燕，戴滨林．双曲元不等式［J］．湘潭大学自然科学学报，1998，20（2）：13－15．

［11］ 王键，戴滨林．离散Möbius群不等式［J］．湘潭大学自然科学学报，1996，18（4）：27－30．

Jφrgensen’s Inequalities in Higher Dimensions

LI Chang－Jun，KONG Yu－Jin
（School of Mathematical Science，Ocean University of China，Qingdao 266100，China）

This paper deal with the relationship between the fixed points and traces of commutator of f and g when they have a common fixed point and f was hyperbolic or strictly parabolic in two－generator groups of Möbius transformation．By using Clifford matrix，an necessary and sufficient condition when they are equivalent was obtained and it was concluded that Jφrgensen inequalities in higher dimensions was still correct when commutator of［f，g］is strictly parabolic．

Clifford matrix；commutator；Jφrgensen inequalities；elementary subgroups

O18

A

1672－5174（2011）05Ⅱ－447－05

留学归国人员启动基金项目（1501－091944）资助

2011－04－01：

2011－04－20

李长军（1965－），男，博士，副教授。研究领域：复分析，离散群几何。E－mail：changjunli7921＠hotmail．com

AMS Subject Classfications： 20H10，30F40，15A66，37C25，30G25

责任编辑 朱宝象