美国国债市场与石油期货市场尾部相关性分析——基于Copula函数的视角

刘湘云，高明瑞

（广东商学院金融学院，广州 510320）

美国国债市场与石油期货市场尾部相关性分析
——基于Copula函数的视角

刘湘云，高明瑞

（广东商学院金融学院，广州 510320）

分别利用单参数和双参数的阿基米德族Copula函数对美国国债市场与纽约石油期货市场之间的尾部相关性进行分析，并与美国股票市场与石油期货市场之间的尾部相关性进行比较。实证分析结果表明，在描述美国国债市场、股票市场与石油期货市场之间的尾部相关性方面，双参数的阿基米德族Copula函数具有更好的拟合效果;美国国债市场与石油期货市场之间具有非对称的尾部相关性，上尾相关性虽然很小，但比下尾相关性大，下尾相关系数几乎为零。

尾部相关性;Copula函数;国债市场;股票市场;石油期货市场;标准普尔500指数;美国

美元作为石油交易的计价货币，其价值的高低必然会影响石油的价格。美国政府每年发行的巨额国债，同样也受到美元价值的影响。两者之间存在什么样的关系以及在什么情况下两者关系会加强，已成为现在投资者所关心的问题。一般认为，美国政府由于财政赤字压力发行巨额国债，在一定程度上导致美元贬值，国债收益率升高。在外汇市场上，由于美元疲软导致石油价格上升，而以其他货币购买时则表现为价格下降、收益率上升。美元升值使得其他国家购买美国国债的价格上升、收益率下降;同样，由于美元的升值，使得其他国家购买石油时价格上升、收益率下降。因此，研究美国国债市场与石油期货市场之间的尾部相关性对投资者有重要的参考意义。

一、文献综述

随着现代金融的快速发展，金融市场之间的关系日益复杂，为了发现其中的相关结构，国内外学者对此领域进行了广泛研究。尾部相关性研究是为了考察一个市场暴涨（暴跌）时，是否会引起另一个市场暴涨（暴跌）。与两个市场在正常时期的相关性相比，在市场急剧上涨或下跌的过程中，两个市场之间的相关结构可能会出现一定的变化，而这种相关结构通常会表现为非对称的尾部相关性。在这次的次贷危机下，一些流行的模型比如VaR的局限性被凸显出来［1］，在这种情形下，在描述随机变量之间相关结构方面具有更大优势的Copula函数成为了研究热点。

在描述金融市场之间的尾部相关性方面，近年来国内外很多学者都进行了研究。根据国内外学者的研究方法，可以把对尾部相关性的研究分为以下几个方面:

（1）利用秩的极大似然方法进行研究的文献:任仙玲、张世英（2008）利用基于秩的极大似然法估计双参数非对称BBX-Copula函数，对民生银行和浦发银行这两只股票的尾部相关性进行实证分析，得出股票市场在低迷时期的尾部相关性高于活跃时期的尾部相关性的结论［2］。王晓芳、谢金静（2009）利用基于秩的极大似然估计法分别采用静态和动态Copula函数对比研究了上证综指和新加坡海峡时报指数收益序列的尾部相关关系，结果发现时变Copula函数两市股指收益序列的尾部相关关系不对称，存在显著的下尾相关，而上尾相关不明显，而且上证综指和海峡时报指数收益序列的下尾相关系数是不断变化的，呈现出日益上升的趋势［3］。

（2）在利用非参数方法进行研究方面:李悦、程希骏（2006）采用非参数估计方法估计Gumbel Copula函数并对上证指数和恒生指数的尾部相关性进行研究，结果表明两者存在上尾相关性［4］。Matthias Fischer和Marco DÄorflinger（2006）利用特殊的回归过程和混合Copula函数提出了新的对尾部相关性进行研究的非参数估计方法［5］。

（3）在利用两步法构建 Copula函数方面: Helder和Luiz（2006）利用条件Copula函数动态地研究了金融资产间的相关结构［6］。韦艳华、张世英（2005）通过构建具有尾部变结构的RS-Copula-GARCH模型，对我国沪深两市非对称尾部相关性进行了研究，并得出两市在上尾部和下尾部的相关关系趋向于增强，并且在下尾部的相关性比上尾部更大的结论［7］。LeoMichelis和CathyNing（2008）利用Copula函数描述了加拿大股票市场和美元兑加拿大元汇率之间的相关结构问题，结果表明两者之间的左尾相关性大于右尾相关性，同时发现它们的尾部相关性呈现动态变化的特征［8］。

（4）在利用半参数估计Copula函数进行研究方面:Claudia Kluppelberg和Gabriel Kuhn（2008）利用半参数的估计方法对多元尾部相关性进行了研究，并发现半参数估计方法比经验尾部相关性估计方法在理论和实践两个方面都要有优势［9］。Cyril Caillault和Dominique Guegan（2003）采用非参数和半参数估计方法，利用Copula函数对亚洲股票市场尾部相关性进行了研究，发现泰国和马来西亚股票市场之间具有对称的尾部相关性，而泰国和印度尼西亚及马来西亚和印度尼西亚股票市场之间存在非对称的尾部相关性，并在最后提出了选取最优 Copula函数进行研究的两种方法［10］。ZsoltTulassay（2008）利用行为模式和经验拟合的途径研究了金融资产利益回报之间的尾部相关性，提出了一个研究资产收益之间尾部相关性的新方向［11］。

从上述文献中可以发现，对Copula函数的参数估计方法主要有半参数估计法、非参数估计法以及极大似然估计法等。上述文献在选用模型的时候，主要是根据模型的特性或者金融市场的特性选取一个合适的模型，或者比较所选择模型的优劣，然后选取最优的一个。根据前人对Copula函数特性的研究可以发现，阿基米德族Copula函数对尾部相关性的描述具有最优性，而前文在选取阿基米德族函数的时候只是简单地选择了单参数或者双参数的Copula函数。因此，本文分别选取了单参数和双参数的阿基米德族Copula函数，利用基于秩的极大似然估计法估计模型的参数来研究美国国债市场和石油期货市场之间的尾部相关性，并与美国股市和石油期货市场之间的尾部相关性进行比较。

虽然Copula函数在刻画金融市场相关结构方面具有重要作用，但是选择合适的Copula函数是其中的关键。因此，正确刻画金融市场之间的相关结构首先要解决的问题有以下两点:

（1）Copula函数的选择问题。不同的Copula函数对相同数据的拟合结果往往存在很大的差异，因此很多学者在对金融市场进行研究的时候采用的模型会不同，但大多数都是根据Copula函数的特性进行选择，也有些是对不同的函数进行数据拟合，然后选择拟合优度最好的Copula函数。

（2）Copula函数的参数估计问题。现在国外很多论文利用非参数、半参数等方法对Copula函数的参数进行拟合，但是利用极大似然估计法和边缘分布推断法这两种方法最为广泛。我国学者的著作中还是以极大似然法和边缘分布推断法为主要的参数估计方法。本文利用基于秩的极大似然估计法对Copula函数的参数进行估计，并用经验分布函数与拟合的Copula函数对比，以选择最优的Copula函数。

二、二元Copula函数及基于Copula函数的尾部相关系数

1.二元Copula函数的定义

二元Copula函数是指具有以下性质的函数C（·，·）:

（1）C（·，·）的定义域为I2，即［0，1］2;

（2）C（·，·）有零基面且是二维递增的;

（3）对任意变量u，v∈［0，1］，满足C（u，1）= u和C（1，v）=v。

假定F（x），G（y）是连续的一元分布函数，令u=F（x），v=G（y），则u，v均服从［0，1］均匀分布，即C（u，v）是一个边缘分布服从［0，1］均匀分布的二元分布函数，且对于定义域内的任意一点（u，v）均有0≤C（u，v）≤1。

Gumbel、Clayton和FrankCopula函数是3类较为常用的二元单参数阿基米德族Copula函数。GumbelCopula函数对变量分布在上尾部的变化十分敏感，能够快速捕捉到上尾的变化。而对于ClaytonCopula函数来说，它与GumbelCopula函数一样，密度函数也具有非对称性，但是它对变量分布在下尾部而不是上尾部的变化十分敏感，能够快速捕捉到下尾相关的变化。GumbelCopula和ClaytonCopula函数只能描述变量间的非负相关关系，而FrankCopula函数还可以描述变量间的负相关关系。由于FrankCopula函数的密度分布成“U”字形，具有对称性，因此无法捕捉到随机变量间非对称的相关关系。而对于阿基米德族双参数Copula函数来说，它弥补了大多数单参数阿基米德族Copula函数不能同时刻画上尾和下尾相关性的缺陷。因此，本文同时利用上面3种常用单参数阿基米德族Copula函数和双参数阿基米德族BB7Copula函数进行实证分析。

2.尾部相关系数

尾部相关系数是一个广泛应用于极值理论的测度，用来表示当一个观测量的实现值为极值时，另一个变量也出现极值的概率。令随机变量X和Y的分布函数分别为F（x），G（x），相应的Copula函数为C（u，v），其中u=F（x）;v=G（y）;u，v∈［0，1］，则

由于当x→∞时u，v→1，因此可以通过分析u，v→1时的条件概率P［U＞u|V＞v］来讨论随机变量X与Y的尾部相关性。其中上尾相关系数为

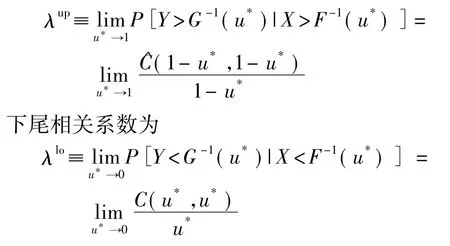
若λup（或λlo）存在且在区间（0，1］内，则随机变量X，Y上尾（或下尾）相关;若λup（或λlo）等于零，则随机变量X，Y独立。

3.Copula函数的估计方法

一般使用的极大似然估计法和边缘分布推断法都属于参数估计法，其不足之处在于Copula函数的参数受到边缘分布函数的影响。由于两个随机变量的相关结构只与它们的相关函数Copula有关而与边缘分布没有关系，因此可以直接利用样本估计Copula函数的参数，这样会更加接近变量间的真实结构。因此，本文采用基于秩的极大似然估计法来估计随机变量之间的Copula函数。

三、实证分析

1.数据描述

本文选取纽约商品交易所石油期货价格指数作为石油期货价格的代表，国债指数选取美国30年、10年国债指数，股票市场指数选取标准普尔500指数，样本区间为1990年10月1日至2009年6月29日。剔除不匹配数据后共有4652个日数据，其中国债指数和标准普尔500指数日收益率来自锐思数据，石油期货指数来自美国能源署（见表1）。

表1 美国国债指数、标准普尔500指数和石油期货指数日收益率情况

从表1可以看出，美国国债指数、标准普尔指数和石油期货指数日收益率均呈现偏峰、厚尾现象，说明美国国债指数日收益率、标准普尔指数日收益率和石油期货指数日收益率均不服从标准正态分布。在收益率均值中，10年和30年国债指数均为负值，虽然标普500指数和石油期货指数收益率为正值却也很小。

2.Copula函数选择及参数估计

对美国30年国债指数日收益率和石油期货指数日收益率的拟合检验结果如表2和图1所示。从表2可以看出，在给出的Copula函数中，BB7函数的对数似然估计值为42.7843、AIC值为-81.5685，而对下尾描述更加精确的Clayton Copula函数、适宜描述上尾相关性的GumbelCopula函数和适宜描述对称结构变量之间相关关系的FrankCopula函数的拟合结果均差于BB7函数，说明BB7函数对美国30年国债指数日收益率和石油期货指数日收益率的拟合是最好的。同时，在图1给出的经验拟合与BB7函数的累积分布拟合比较中，也可以得出相同的结论。

表2 美国30年国债指数日收益率和石油期货指数日收益率模型拟合检验

图1 美国30年国债指数日收益率和石油期货指数日收益率BB7函数与经验分布函数的拟合优度比较

BB7函数的相关系数如表3所示，由表3可知，BB7函数的Kendall秩相关系数为0.0699，Spearman秩相关系数为0.1041，两个随机变量之间的上尾系数为0.097，下尾系数为0.00001。这表明，美国30年国债日收益率和石油期货指数日收益率之间存在非对称的尾部相关性，上尾相关性比下尾相关性要大，在两个市场同时出现上涨的概率为0.097，同时下跌的概率几乎为零。

表3 美国30年国债指数日收益率和石油期货指数日收益率BB7函数的相关系数

对美国10年国债指数日收益率和石油期货指数日收益率的拟合结果如表4和图2所示。

表4 美国10年国债指数日收益率和石油期货指数日收益率模型拟合检验

从表4可以看出，在给出的Copula函数中，BB7函数的对数似然估计值为38.5066，AIC值为-73.0134，而对下尾描述更加精确的Clayton Copula函数、适宜描述上尾相关性的Gumbel Copula函数和适宜描述对称结构变量之间相关关系的Frank Copula函数的拟合结果均差于 BB7函数，说明BB7函数对美国10年国债指数日收益率和石油期货指数日收益率的拟合是最好的。同时，在图2给出的经验拟合与BB7函数的累积分布拟合比较中，也可以得出相同的结论。

图2 美国10年国债指数日收益率和石油期货指数日收益率BB7函数与经验分布函数的拟合优度比较

BB7函数的相关系数如表5所示，其中Kendall秩相关系数为0.0654，Spearman秩相关系数为0.0976，两个随机变量之间的上尾相关系数为0.085，下尾相关系数为0.00001。这表明，美国10年国债日收益率和石油期货指数日收益率之间存在非对称的尾部相关性，上尾相关性要比下尾相关性大得多，在两个市场同时出现上涨的概率为0.085，同时下跌的概率几乎为零。

表5 美国10年国债指数日收益率和石油期货指数日收益率BB7函数的相关系数

对美国标准普尔500指数日收益率和石油期货指数日收益率的拟合结果如表6和图3所示。

从表6可以看出，在给出的Copula函数中，BB7函数的对数似然估计值为23.8171，AIC值为-43.6342，而对下尾描述更加精确的Clayton Copula函数、适宜描述上尾相关性的GumbelCopula函数和适宜描述对称结构变量之间相关关系的FrankCopula函数的拟合结果均差于BB7函数，说明BB7函数对美国标准普尔500指数日收益率和石油期货指数日收益率的拟合是最好的。同时，在图3给出的经验分布函数与BB7函数的累积分布拟合比较中，也可以得出相同的结论。

表6 美国标普500指数日收益率和石油期货指数日收益率模型拟合检验

图3 美国标普500指数日收益率和石油期货指数日收益率BB7函数与经验分布函数的拟合优度比较

美国标普500指数日收益率和石油期货指数日收益率BB7函数的相关系数如表7所示，其中Kendall秩相关系数为0.0483，Spearman秩相关系数为0.0721，两个随机变量之间的上尾相关系数为0.0445，下尾相关系数为0.00001。这表明，美国标准普尔500指数日收益率和石油期货指数日收益率之间存在非对称的尾部相关性，上尾相关性要比下尾相关性大得多，在两个市场同时出现上涨的概率为0.0445，同时下跌的概率几乎为零。

表7 美国标普500指数日收益率和石油期货指数日收益率BB7函数的相关系数

四、结 论

金融市场之间的线性相关并不能说明它们之间复杂的关系，本文运用可以描述金融市场之间非线性关系的Copula函数对美国国债市场、股票市场与纽约石油期货市场收益率之间的尾部相关性进行了实证分析。在给出的单参数和双参数Copula函数中，可以发现双参数的Copula函数与本文开始提及的Gumbel、Clayton函数相比，在对数据之间的尾部相关性描述方面具有更好的效果。同时，根据尾部相关系数，可以得出美国国债市场与纽约石油期货市场之间具有微弱的非对称尾部相关性，其中下尾相关系数几乎为零，上尾相关系数不到0.1。作为对比，美国股票市场与纽约石油期货市场之间的尾部相关性也呈现出非对称的相关性，表现为上尾相关性明显高于下尾相关性。以上研究只是表明美国国债市场与石油期货市场之间具有非对称的尾部相关性，在进一步的研究中，新兴市场的国债市场与石油期货市场以及其他发达市场的国债市场与石油期货市场之间的尾部相关性将是研究的重点。

［1］李裕丰，罗丹程，王赫.基于VaR方法的金融风险度量模型及其应用［J］.沈阳工业大学学报:社会科学版，2009（4）:335-339.

［2］任仙岭，张世英.基于Copula函数的金融市场尾部相关性分析［J］.统计与信息论坛，2008（6）:66-71.

［3］王晓芳，谢金静.基于多种Copula函数的沪新股市尾部相关性比较分析［J］.统计与信息论坛，2009，24（6）:27-32.

［4］李悦，程希骏.上证指数和恒生指数Copula尾部相关性分析［J］.系统工程，2006，24（5）:88-92.

［5］Matthias F，Marco D. A note on a non-parametric tail correlation estimator ［R］. Nuremberg，Germany:Department of Statistics and Econometrics，Friedrich Alexander University of Erlangen-Nuremberg，2006: 1 -4.

［6］Helder P P，Luiz K H. Using conditional copula to estimate value at risk ［J］. Joumal of Data Science，2006，4(1) : 93-115.

［7］韦艳华，张世英.金融市场非对称尾部相关结构的研究［J］.管理学报，2005，2（5）:601-605.

［8］ Leo M，Cathy N.Correlation structure between the Canadian stock market and the US/Canada exchange rate: a copula approach ［EB/OL］.［2008-05-11］.http://www.soegw.org/files/program/95-Michelis%20Ning. pdf.

［9］Claudia K，Gabriel K，Liang P. Semi-parametric models for the multivariate tail correlation function: the asymptotically dependent case ［J］. Scandinavian Journal of Statistics，2008，35(4) : 701-718.

［10］Statistics，2008，35(4) : 701 -718.［10］Cyril C，Dominique M G. Empirical estimation of tail correlation using copulas: application to Asian markets［J］. Quantitative Finance，2005，5(5) : 489 - 501.

［11］］Zsolt T. Tail dependence of financial returns: empirical investigation and a behavioral model ［R］. Budapest，Hungary: CAMEF Budapest workshop，2008: 1-24.

Analysis on tail correlation between governmental bond market and oil futures market in the United States of America:from perspective of Copula function

LIU Xiang-yun，GAO Ming-rui
（School of Finance，Guangdong University of Business Studies，Guangzhou 510320，China）

One and bivariate parameter Archimedean Copula functions are used to analyze the tail correlation between the US governmental bond market and the New York oil futures market.The results are compared with the tail correlation between the US stock market and oil futures market.When the tail correlation is estimated between bond market，stock market，and oil futures market，the bivariate Archimedean Copula function has better fitting result.There is asymmetrical tail correlation between US governmental bond market and oil futures market，though the upper tail correlation is small，but it is stronger than lower tail correlation，while the lower tail correlation is almost zero.

tail correlation;Copula function;governmental bond market;stock market;oil futures market; Standard＆Poor’s 500 index;United States of America

C812;F831.5

A

1674-0823（2011）01-0032-06

2010-04-16

中国博士后科学基金项目（20090450627）;广东省自然科学基金项目（8151032001000006）。

刘湘云（1972-），男，湖南衡阳人，教授，博士后，主要从事金融风险管理和金融工程等方面的研究。

（责任编辑:吉海涛）