数学操作活动的误区及对策
2010-12-29吴志行
小学教学参考(数学) 2010年12期
在小学数学课堂教学中,组织学生进行有效的操作活动,不仅能激发学生的学习兴趣,促进学生参与学习过程,还能帮助学生理解数学概念或数理关系,促进知识内化,发展数学思维。
对于数学课堂中操作活动的价值,大多数教师是认同的,并在课堂中组织学生进行操作活动。但是,当前小学数学课堂中的操作活动仍存在着一定的误区。如有的教师对操作活动的目标不明确,活动组织不科学,活动评价不恰当,致使操作活动的效果大打折扣,或成为无效操作,甚至产生了负面效应。基于此,本文就小学数学课堂教学中操作活动的误区与对策作简要分析。
误区一:材料不当,导致结果偏差
案例:一位教师在教学“可能性”时,组织学生做抛正方体的操作活动。教师为每个组都准备一个正方体木块,木块的6个面分别写着1~6这六个数字,任意抛30次,记录每个面朝上的次数,以此来研究等可能事件。可是,教师为学生准备的正方体木块太大了,学生从有限的距离抛下后,正方体木块翻滚不起来,也就是说,抛之前哪个面朝上,抛到桌面上一般还是这个面朝上。因此,操作的结果可信度不够,很多组根据操作后记录的数据看不出“每个面朝上的可能性差不多”,尽管教师为此做了很多解释,学生还是一脸的茫然。
对策:细致准备,精心策划过程
操作活动必须借助一定的材料来完成,因此操作材料的选择是否恰当对操作的完成情况起着重要作用。教师在准备操作活动的材料时,一定要从科学性、可行性等方面进行分析,充分考虑材料的大小、颜色、质地等因素。如果让学生自己准备材料,一定要说明材料的具体要求。必要的时候,教师还需在课前进行“下水”操作,从操作的可行性、花费的时间、获取结果的有效性、可能出现的问题等方面进行分析,及时调整操作活动的计划。
如特级教师华应龙在教学“可能性”时,也设计抛正方体的试验。为了充分体现“抛”的随机性,他没有让学生直接抛正方体骰子,而是让学生把正方体放到圆柱形的杯子中,通过摇动杯子使里面的正方体抛起来,使正方体抛的高度不至于太高或太低,抛的力度不至于太重或太轻。他为了购买平底、上下同样精细、高度约30厘米的杯子,跑了很多商场,反复比较,细致挑选,之后又对操作过程精心预设,因此生成了课堂教学的精彩。
误区二:目标游离,导致形式主义
案例:一位教师在教学“可能性”时,设计了这样的操作活动:在一个布袋里放入8个红球和2个白球,从中任意摸一个球,以此获得“摸到红球的可能性比较大”的结论。课堂上,教师先让学生猜想:如果任意摸20次,摸到哪种球的次数比较多?大多数学生猜想“摸到红球的次数比白球的次数要多”,这一想法正合教师之意,因此给予了表扬。可是,也有学生这样猜想“摸到两种球的次数有可能一样多”,这种想法马上被教师否定了。在接下来的分组操作活动中,有一组学生意外地出现了摸到两种球的次数同样多这种“小概率”情况,他们便认为这次操作是“不成功的”,把刚刚进行的记录全部擦掉了,于是又重新操作了一次,终于得到了“满意的结果”。
对策:正确定位,辩证处理关系
为什么要操作?操作活动的目标是什么?这是每位教师在指导学生进行操作活动之前必须思考的问题。一般来说,操作活动是为探究提供必要的数据,或者获得感性的认识。在动手操作之前,可引导学生对操作的结果进行猜测,然后通过操作活动进行验证。但是,运用“猜想——验证”的策略一定要处理好二者之间的关系。如上述案例中,教师已经暗示了最后的结论,导致操作活动成了可有可无的点缀,流于形式。
需要教师引起注意的是,先前的“猜想”不能束缚后面的“操作”,教师不能因为“先知”,有意或无意地暗示学生所谓正确的结果,应允许学生生成不同的猜想,甚至暂时存在错误的想法,这样猜想后的操作活动才显得有意义,学生也更有操作热情。为此,教师要让学生认识到:猜想可能是正确的,也可能是错误的,操作活动的结果可以用来证明猜想是正确性的,也可以用来证明猜想是错误的。同时,教师还要让学生知道,有限次的操作也可能存在局限性,有可能出现“小概率”事件,但只要操作过程符合操作要求,其结果都是可取的,不可以随意地对操作结果进行更改。
误区三:指导不力,导致认识模糊
案例:一位教师在教学“观察物体”一课时,让学生把长方体木块放在桌子上,问从同一个角度观察,最多能看到几个面。一些学生不明白何谓“从同一个角度”观察,观察时不能做到视线角度不变。有的学生还把从不同位置看到的情况累加起来,得到的结果是除了最下面的面,其他的面都能看得到,也就是最多能看到5个面。集体交流后,教师没有认真分析学生产生错误的根本原因,而是按照预设的教案,用摄像头从不同位置拍摄出长方形木块的图片,通过投影让学生再观察拍摄到的视图。可是,这些使学生的认识却越来越模糊,无奈只得“承认”最多能看到3个面。
对策:重视主导,讲求引导艺术
在组织操作活动中,教师要有针对性和明确的指导,如让学生明白做什么、用什么做、做的时候有什么要求等等。教师的指导性语言要明确、清晰,切忌含糊不清。如上述案例中,操作活动之前,教师的组织引导不够,没有让学生弄清观察要求,特别是没有指导学生分辨日常生活中的“看”与数学上的“观察”有什么不同,导致学生观察结果的错误。而用摄像头代替学生的“眼睛”观察,这样处理同样没有抓住问题的实质,导致学生的认识越来越模糊。
北师大肖川博士曾经说过:让学生“动”起来是课程改革的一个目的,但光“动”起来是远远不够的。“动”得不好就会“乱”,是停留在表面上的热闹,而实质上并没有带给学生理智的挑战、认知上的冲突、内心的震撼和无言的感动。“活而不乱”才是新课程背景下课堂教学追求的理想目标。因此,在操作活动之前,教师既要把操作活动的要求说清楚,还要用恰当的方式显现,使学生乐于去听。只有学生明确了操作要求,操作活动才能真正有效。对于学生出现的错误,教师要认真分析原因,处理好预设与生成的关系,灵活调节,同时注意讲究引导的艺术。如上述案例中,教师不必用学生并不太熟悉的摄像头来辅助教学,可让一名出现错误的学生到前面来观察实物,师生就其观察方法进行评点,相信不难解决这个问题。
误区四:机械操作,缺少思维含量
案例:借助操作探索圆锥的体积计算公式,教师让学生准备好等底等高的圆柱和圆锥形容器。(有的教师为了便于教学,全班学生准备统一的圆柱与圆锥形容器)在教师的指令下,学生用圆锥形容器盛物倒入圆柱形容器中,正好三次可以倒满,这样可得出等底等高的圆锥体积是圆柱体积的三分之一的结论,因此很顺利地推导出圆锥的体积计算公式。
对策:发挥自主,操作思维并行
上述案例看上去没有什么问题,学生通过操作活动,明确了等底等高的圆锥体积是圆柱体积的三分之一,继而推导出圆锥体积计算公式,完成了教学任务,而且教学效率很高。但是仔细分析不难看出:学生是在教师指令下,一步一步地完成操作活动,只是被动地将学具搬来移去,抹杀了学生的创造性。学生对为什么要操作,通过操作活动可以达成什么目的则茫然不知,这种心中无目标的操作比起不操作来并无多大差异。因此,教师不妨让学生多准备几个不同的圆柱和圆锥形容器,其中有等底等高的圆柱与圆锥,也有等底不等高的圆柱与圆锥,还有底与高都不相等的圆柱和圆锥。学生通过多次操作,记录相关数据,再从众多的数据出发寻找联系。这样进行的操作活动,才是学生自主探究的活动,才是与思维同行的活动。
误区五:评价偏颇,导致虚假操作
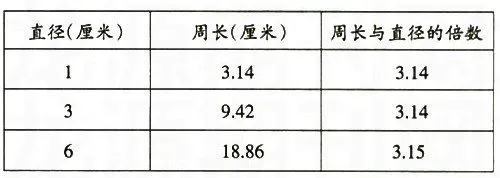
案例:一位教师在教学“圆的周长”一课时,引导学生测量圆的直径与周长,并计算出圆的周长与直径之间的倍数关系。下面是一位学生操作后的结果:
教师对这位学生的测量结果给予了极高的评价。其实,细心的教师就会发现:学生对圆周率已经有了一定的认识,表格中的数据明显是学生刻意“制造”出来的,因为用普通的直尺测量时,以厘米为单位,是无论如何测量不出精确两位小数的数值的。不仅如此,学生似乎为避免教师看上去数据是制造出来的,还“制造”出周长是直径的3.15倍的数据。
对策:注重过程,恰当运用评价
有的教师为了课堂教学的顺利进行,过分看重操作活动的结果,对符合教学预期的操作结果给取肯定、表扬,对不符合教学预期的操作结果否定、批评,而不从操作活动的过程给予评价。长此以往,一些学生摸清了教师的“心思”,便会投其所好,制造出符合要求的结果。这样的做法,教师如果不能及时给予否定与制止,其后果是严重的,不仅影响了学生对操作活动科学性、必要性的认识,更不利于学生形成严谨、求实的学习精神,甚至会影响学生健康人格的发展。因此,教师要客观地对待学生操作活动的结果,对误差较大的操作结果要帮助他们寻找原因,指出改正的方法;对“制造”的虚假数据,要旗帜鲜明地给予否定,并帮助他们端正认识;学生在操作活动的过程中,教师要深入到学生之中,了解学生操作活动的真实情况,为操作活动的总结与评价提供第一手资料。
操作活动对课堂学习秩序及学生学习策略提出了挑战,要保证操作活动的效果,教师应充分发挥评价的激励和调控作用,及时、客观地评价学生的操作结果、操作态度等,帮助学生形成良好的行为习惯和价值取向。
(责编杜华)
