MBBM方程的一类精确解

陆 博 刘 娟 杨金库

(河南科技学院数学系 河南新乡 453003)

MBBM方程的一类精确解

陆 博 刘 娟 杨金库

(河南科技学院数学系 河南新乡 453003)

利用齐次平衡法并借助一维立方非线性Klein-Gordon方程的精确解，将一个难于求解的非线性偏微分方程化为一个易于求解的代数方程组然后用待定系数法确定相应的常数，简洁地求得MBBM方程的精确解。这些解中包含三角函数解，Jacobi椭圆函数解等。同时这种方法还可以可应用于其他的非线性发展方程的求解.

MBBM方程;维立方非线性Klein-Gordon方程;齐次平衡法;精确解

0 引言

随着科学技术的发展，非线性问题的研究在自然科学和社会科学领域的作用越来越重要。物理、化学、生物、工程技术，甚至经济研究等都存在着大量的非线性问题，这些问题可用非线性常微分方程或非线性偏微分方程来描述。因此，如何求解这些非线性方程成为广大数学和科技工作者致力于研究的一个重要课题。非线性发展方程在力学、物理学和其他学科的许多分支中有广泛的应用。寻找其解有着非常重要的意义。近年来各种寻找偏微分方程解的方法已得到发展，为人们提供了直接寻找非线性偏微分方程精确解的新途径。

近年来，人们对非线性发展方程的行波解很感兴趣，这是因为行波解能够较好地描述非线性物理现象，如流体动力学中的波现象、光纤维现象等。关于行波解的求法是目前孤立子理论的一个重要研究方向，比如有tanh函数法、sine-cosine法、Jacobi椭圆函数展开法［1-2］等。齐次平衡法也是寻求非线性发展方程行波解的最直接而有效的方程之一［3-4］。

1972年 Benjamin T.B.Bona J.L.和 Mahony J.J.把Benjamin-Bona-Mahony方程，简记为BBM方程作为KdV方程的精确解提出的［5-6］。从那时起对于各种广义的BBM方程的周期边界问题初值问题和初边值问题被广泛研究［5-9］。本文利用齐次平衡法求出了MBBM方程的精确解。

1MBBM方程的求解

考虑如下形式的MBBM方程［9］

令u=u(x，t)=u(ξ)，其中ξ=ax+bt+ξ0，a，b为待定常数，ξ0为任意常数。

将u=u(x，t)=u(ξ)代入方程(1)式经整理可得:

其中“u′”表示对ξ求导数“u‴”表示对ξ求三阶导数。

将(2)式两端积分一次并取积分常数为零可得方程:

下面平衡方程(3)中的最高阶非线性项与最高阶导数项并求解。

令u=a0+a1φ+…+anφn，其中φ(ξ)满足一维立方非线性Klein-Gordo方程:

由方程(3)可知u=a0+a1φ+…+anφn的非线性项次数为3n最高阶导数项为(φn)=n(n-1)φn-2(φ′)2+nφn-1φ″，由方程(4)可知φ″与φ3等价故可得到:n=1。则

将方程(5)和方程(4)代入(3)得到:

再令上述方程中的φ(ξ)的各幂次项系数为零可得到一个代数方程组:

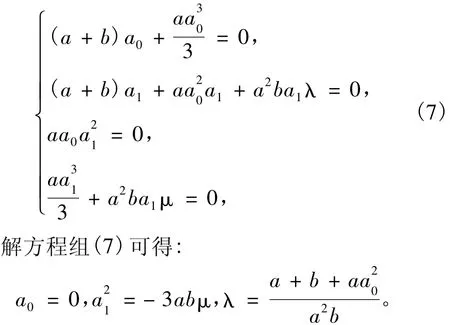
于是可得到MBBM方程(1)的精确解形式为:

2 MBBM方程的精确解举例

利用文献［5］所给的一维立方非线性 Klein-Gordon方程的各种精确解可得到方程(1)的几种精确解。

其中ξ=ax+bt+ξ0，a，b，ξ0，β为任意常数。

其它情况可参见文献［10］所提供的方法求解，从而求得在不同情形下MBBM方程的精确解。

3 结束语

本文利用齐次平衡法并借助于一维立方非线性Klein-Gordon方程的精确解，求出MBBM方程的精确解。该方法具有一定的普遍性，可用于求解更多的非线性发展方程。

［1］ Fan Engui.Extended tanh-function method and its applications to nonlinear equations［J］.Phys Lett A，2000，277:212-218.

［2］ 刘式适，等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用［J］.物理学报，2001，50(11): 2068-2073.

［3］ Wang Ming liang.Solitary wave solution for variant Boussinesq equations［J］.Phys Lett A，1995，199: 169-172.

［4］ Lou Senyue，Guang jiong.Ni Physics Department［M］，Shanghai:Fudan University，2002.

［5］ P Biler.Long time behavior of solutions of the generalized Benjamin-Bona-Mahony equation in two space dimensions［J］.Diff Integral Egns，1992，5:891-901.

［6］ J Albert.Dispersion of low energy waves for the generalized Benjamin-Bona-Mahony equation［J］.J differential Equations，1986，63:111-134.

［7］ Zhang L H.Decay of solutions of generalized Benjamin-Bona-Mahony equations［J］.Acta Math Sinica，1994，10:428-488.

［8］ 陆博，李巧萍.Boussinesq-Schrödinger方程组的精确解［J］.河南工程学院学报，2009(4):53-56.

［9］ Benjamin T B，Bona J L，Mahony J.J..Model equations for long waves in nonlinear dispersive systems［J］.Philos Trans Roy SocLondon Ser A1972，272:47-78.

［10］ Medeiros L A，Menzala G Perla.Existence and uniqueness for periodic solutions of the Benjamin-Bona-Mahony equation［J］.SIAM J Math Anal，1977，8:792-799.

A Class of Exact Solutions of the MBBM Equations

LU Bo LIU Juan YANG Jin-ku
(Department of Mathematics，Henan Institute of Science and Technology，Xinxiang 453003，China)

Using the homogeneous balance method and the accurate solution of one-dimensional cubic nonlinear Klein-Gordon equation as a class of nonlinear partial differential equations that are hard to be solved by the usual ways can be reduced to a set of easily solved algebraic equations，and their related coefficients can be easily determined by the undetermined coefficients method.Then，the exact analytical solutions of MBBM equation can be obtained.These solutions contain triangular periodic solutions，Jacobi elliptic function solutions and so on.The approach presented in the paper may be used to other nonlinear evolution equations for generating solutions.

MBBM equation;one-dimensional cubic nonlinear Klein-Gordon equation;homogeneous balance method;exact solution

O 175.29

A

1672-2434(2010)06-0031-02

2010-09-06

陆 博(1981-)，男，助教，硕士，从事研究方向:偏微分方程