空间站组合体惯性系内角动量管理控制*

2010-12-11马艳红何英姿

空间控制技术与应用 2010年6期

关键词：角动量惯性气动

张军，马艳红, 何英姿

(1.北京控制工程研究所, 北京 100190; 2.空间智能控制技术重点实验室，北京100190)

空间站组合体惯性系内角动量管理控制*

张军1,2，马艳红1,2, 何英姿1,2

(1.北京控制工程研究所, 北京 100190; 2.空间智能控制技术重点实验室，北京100190)

针对惯性系内重力梯度力矩与气动力矩的常值部分积累引起控制力矩陀螺饱和的问题，在惯性系内建立空间站的动力学模型并进行线性化，利用滤波变量将系统状态方程扩维，采用LQR方法设计系统反馈控制增益矩阵，实现空间站在惯性系内的角动量管理控制.惯性系内重力梯度力矩、气动力矩由轨道角速度整数倍的频率成份构成，可以根据实际情况增加抑制不同频率成份的滤波变量，用于抑制不同频率成份干扰力矩对空间站姿态或控制力矩陀螺角动量的干扰，从而使空间站长期在惯性系内飞行而不需要进行角动量的卸载.仿真验证了控制器的性能.

空间站；惯性坐标系；角动量管理；控制力矩陀螺

空间站的突出特点是由多个舱段在轨组装而成，从而导致其质量和惯量很大，如“和平”号空间站最大主转动惯量接近1×107kg·m2，国际空间组装完成后，最大主惯量达到2×108kg·m2.

传统航天器在轨飞行时保持三轴对地稳定，采用磁力矩器或喷气进行角动量卸载.由于空间站的惯量大，在轨道系内保持三轴稳定飞行时，其常值姿态偏差及惯量积导致的重力梯度力矩、气动力矩将引起非常快的角动量积累，如国际空间站最大气动力矩达到8.8N·m.如此大的外干扰力矩引起的角动理积累不可能采用磁力矩器来完成卸载，因此国际上，空间站均利用重力梯度力矩来进行角动量的管理.

礼炮6号与礼炮7号没有安装控制力矩陀螺(CMG,control momnet gyros)，它们长期采用重力梯度力矩被动稳定的飞行模式，但这导致空间站的姿态偏差很大(±35°～40°)，能源也非常有限[1].

第三代空间站(“和平”号、国际空间站)均采用主动姿态控制.“和平”号空间站利用主惯性轴垂直于轨道平面时重力梯度力矩不积累、气动力矩基本不积累的特点，在惯性系内进行姿态保持，但它具体的控制方法未见诸文献.“和平”号空间站采用两种惯性姿态，一种是将靠近纵轴的主惯性轴垂直于轨道面，其他两个惯性主轴之一指向太阳在轨道面内的投影；另一种为侧向的两个主惯性轴之一垂直于轨道面，靠近纵轴的主惯性轴指向太阳在轨道面内的投影[2-3].

国际空间站(ISS,international space station)组装早期也采用“和平”号的飞行模式，在惯性系内进行角动量管理.ISS组装后期在轨道系内飞行，采用力矩平衡姿态(TEA,torque equilibrium attitude)的思想，利用三轴姿态实时调整，达到重力梯度力矩与气动力矩在轨道周期内的平衡，三轴姿态活动范围为±15°[4].

“和平”号和国际空间站的方案各有利弊.在轨道系内进行角动量管理，实际上是利用重力梯度力矩来平衡气动力矩，因此空间站的惯量特性必须满足一定约束条件，即其主惯性轴必须相差较大，才能产生足够的重力梯度力矩来平衡气动力矩；在惯性系内进行角动量管理，重力梯度力矩与气动力矩只周期性波动，不会积累，但要求CMG的容量较大[5].

本文研究空间站在惯性系内进行角动量管理的控制器设计问题.空间站在惯性系内飞行时，为了让重力梯度力矩不积累，必须保证空间站的某一主惯性轴严格垂直于轨道面，但实际工程上主惯性轴的指向并不明确，而同时气动力矩的增长部分也必须依靠重力梯度力矩来平衡.本文采用角动量反馈的方法，在线性化方程中引入滤波变量，能抑制任意轨道角速度频率的整数倍成份对姿态或角动量的影响，抑制CMG饱和，达到长期进行角动量管理的目的.

1 动力学模型

定义轨道坐标系ooxoyozo原点在空间站质心，xo指向飞行方向，zo指向地心方向，yo与xo、zo按右手规则形成正交坐标系，惯性坐标系oixiyizi在初始时刻与ooxoyozo重合，在惯性空间内保持指向不变.为在惯性系内进行空间站的角动量管理控制，需要在惯性系内描述空间站的动力学.空间站的姿态动力学方程可写为

其中上标i表示在惯性系内，下标s/c表示空间站，右边施加的力矩包括控制力矩、重力梯度力矩与外干扰力矩，可表示为

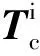
CMG的角动量方程为

重力梯度力矩的表达式为

其中Ji表示oixiyizi内空间站的转动惯量，Ri为地心到空间站质心矢量在oixiyizi内的坐标.

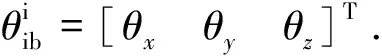
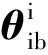
则有

上标b代表本体系obxbybzb.

将Ri、Ji的表达式代入式(4)可得重力梯度力矩的表达式

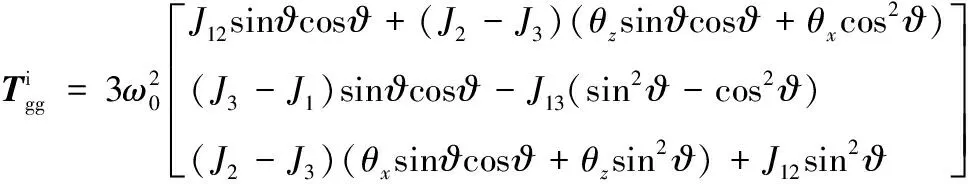
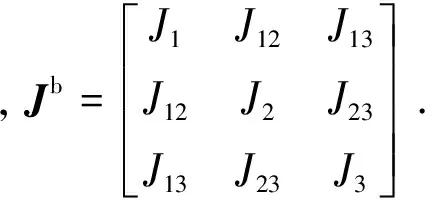
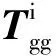
角动量管理控制是利用惯性主轴的指向来产生重力梯度力矩的，因此为进行控制器设计忽略惯量积，可得重力梯度力矩近似为

式(9)可进一步写成

其中，

由空间站的角动量表达式可得运动学方程如下：

方程(1)、(3)和(11)一起描述了空间站及CMG的运动.

2 控制器设计

如上所述，空间站主惯性系不垂直于轨道面时，重力梯度力矩会引起角动量的积累，其他非常值部分频率为轨道频率的整数倍.由于空间站的立体构型及大气方向在轨道系内的周期波动，气动力矩也会引起小幅值的积累.在惯性空间oixiyizi内三轴上常值力矩会引起角动量的积累，必须消除，而单倍和双倍轨道角速度频率成份的干扰力矩虽然不会引起角动量的积累，但由于这两种频率的干扰成份幅值较大，会引起姿态的较大范围波动，因此在控制器设计当中也应当考虑消除它们对姿态的影响.

下面通过引入滤波器，将空间站姿态动力学方程扩维，采用LQR方法，设计相应的反馈控制器，达到抑制空间站外干扰力矩的目的.将系统扩维后，系统动力学方程及控制器如下:

式中,f为滤波状态变量，K为3×24的增益矩阵，x为状态方程的状态变量，式(12)中滤波状态变量的导数可通过设置3×3的矩阵Aih、Aiθ(i=0,11,12,21,22)来定义.设计者通过定义Aih、Aiθ的行变量来消除稳态时相应的空间站姿态或CMG的角动量波动.f0用来消除常值部分，f1用来消除单倍轨道角速度干扰的影响，f2用来消除双倍轨道角速度干扰的影响[2].

本文强调姿态的稳定，即在不引起CMG角动量积累的前提下，尽量减小空间站姿态的抖动，即利用空间站滚动与偏航的姿态进行角动量管理，而俯仰轴的姿态则需要保持稳定，同时要抑制轨道角速度整数倍频率成份的干扰力矩对姿态的影响，因此设置如下形式的Aih、Aiθ矩阵

3 数学仿真

假设空间站惯量及LQR方法中Q、R取值为

上式中，diag{}表示以行变量为主对角元素形成对角阵，11×15为元素为1的1×15的行向量.

空间站运动轨道高度400 km，取太阳活动高年，仿真结果如图 1～图 6所示.图 1为空间站的姿态角速度曲线，图 2为空间站姿态角曲线，俯仰轴最后趋于0°，滚动与偏航轴分别趋于1.5°、2.3°，这是为了消除惯量积引起的常值重力梯度力矩及气动力矩的常值部分引起的角动量积累，由于本文中控制器只抑制了常值、单倍和双倍轨道角速度成份的干扰力矩的影响，频谱分析可以看到，俯仰轴的三倍轨道角速度成份的干扰力矩幅值也达到了1.4N·m，因此该干扰对空间站姿态仍然造成了较大的扰动.图 3、图 4分别为重力梯度力矩与气动力矩引起的角动量积累，可以看到，滚动轴两种外干扰引起的角动量积累方向是相反的，最后导致合成的角动量并不积累，其他两轴干扰力矩都不积累.图 5、图 6分别为CMG的控制力矩与角动量，可以看到CMG的角动量并不积累，说明控制器达到了角动量管理的目的.

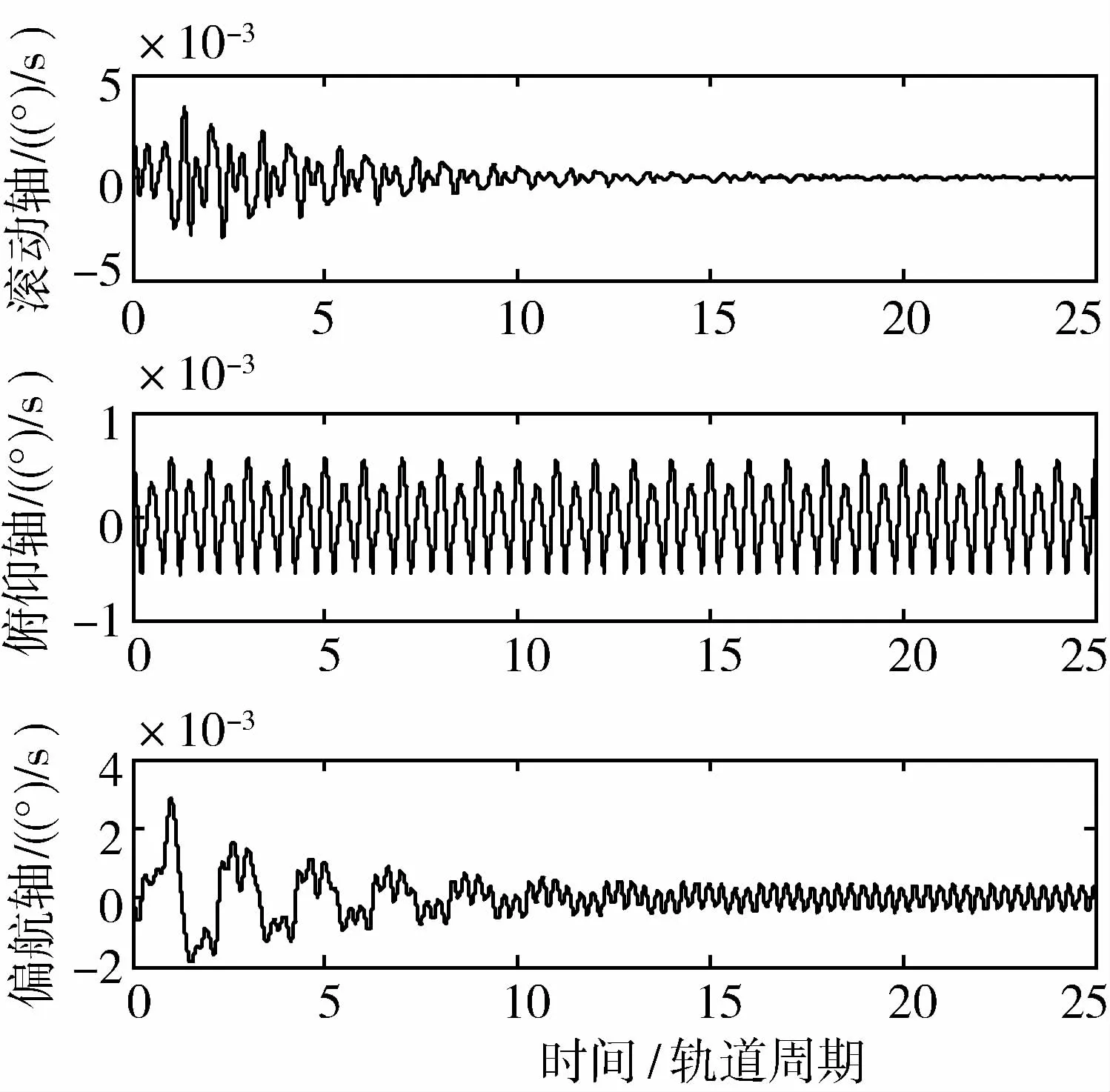
图1 空间站三轴姿态角速度

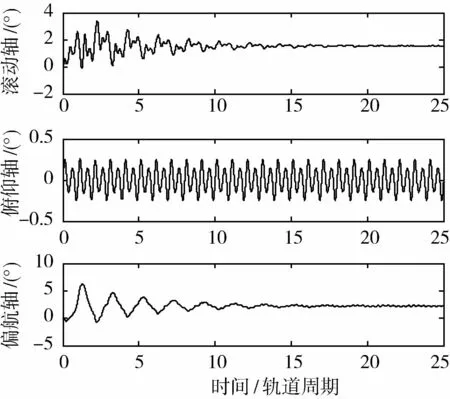
图2 空间站三轴姿态角

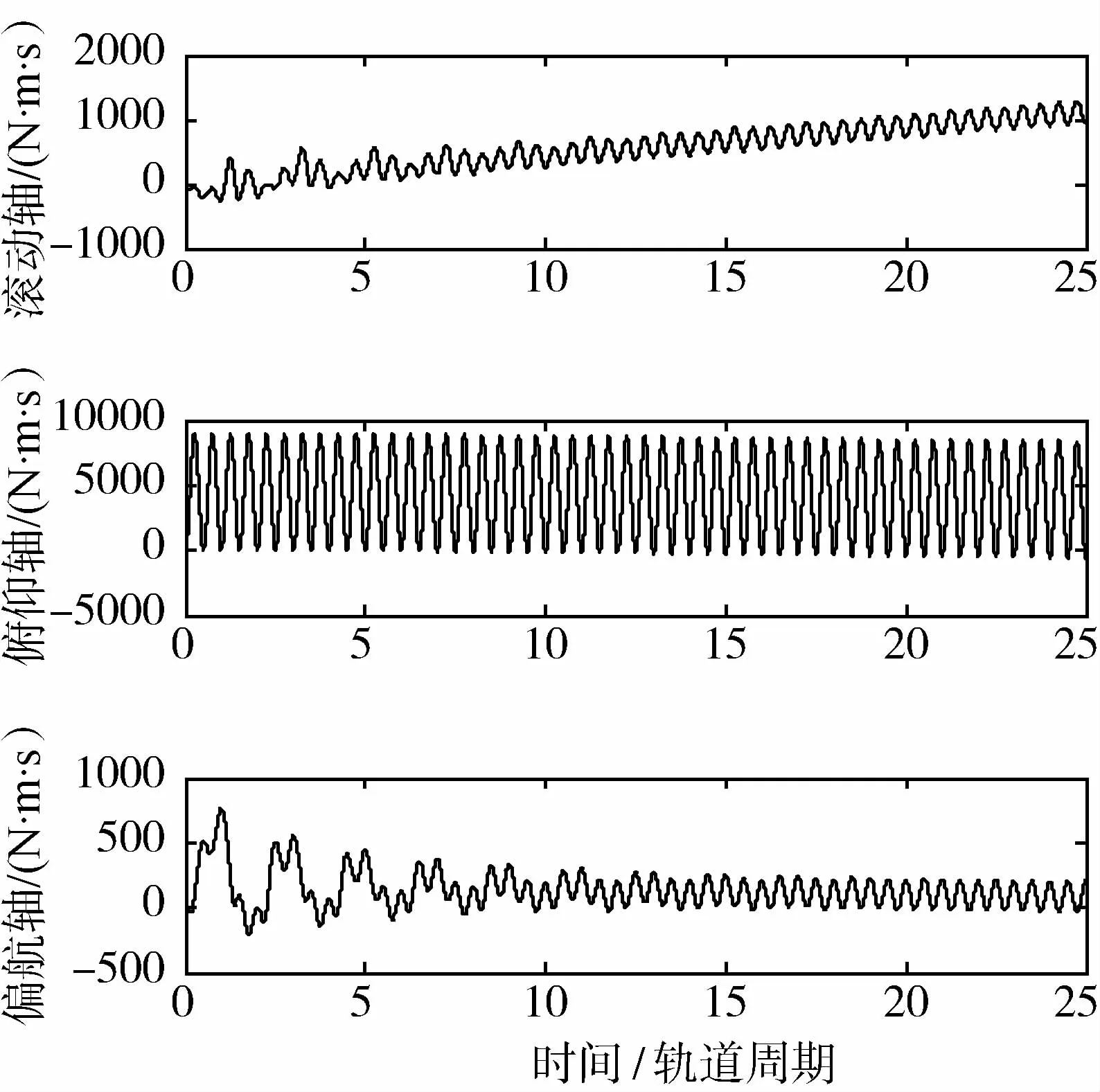
图3 重力梯度力矩引起的角动量积累

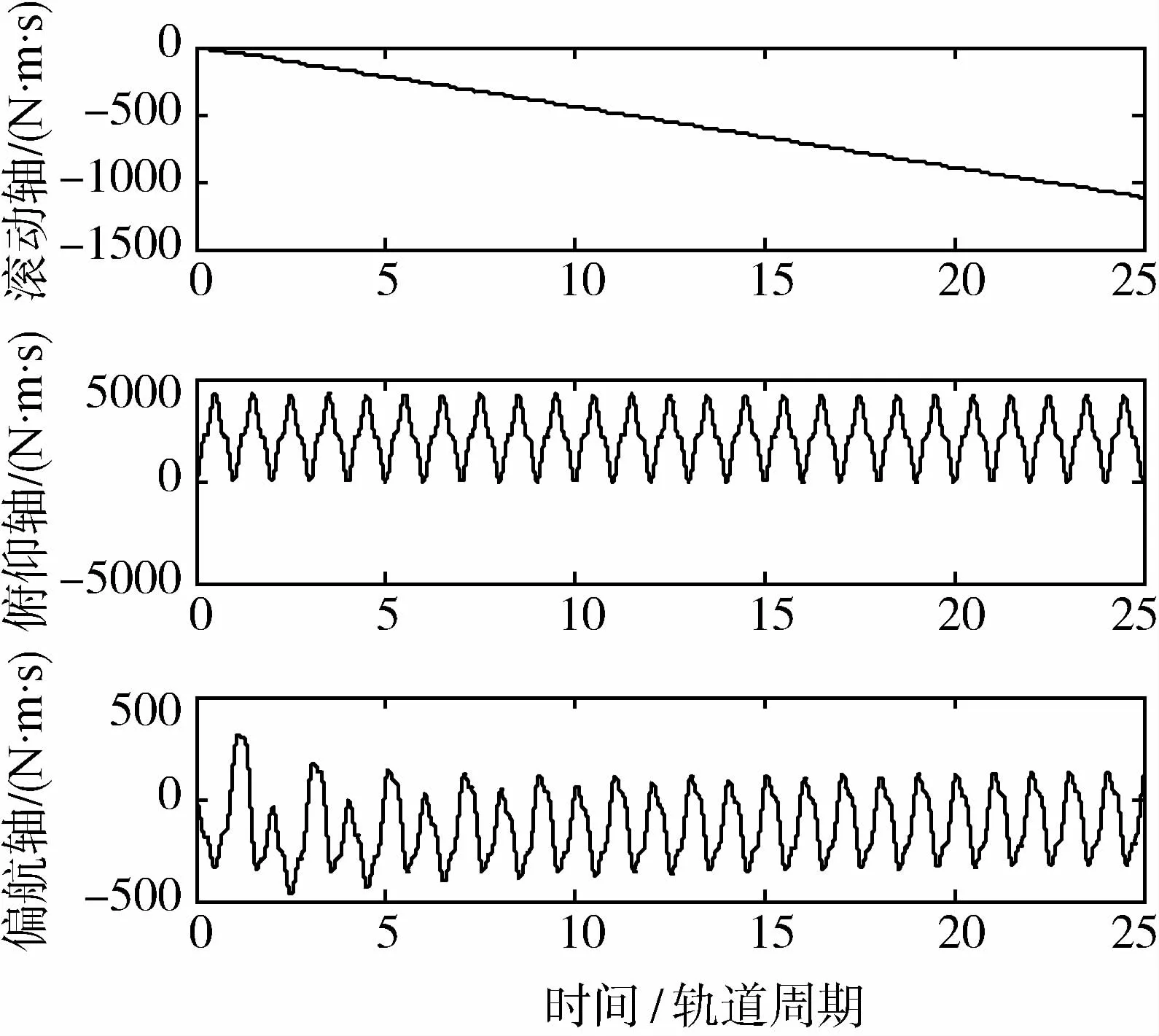
图4 气动力矩引起的角动量积累

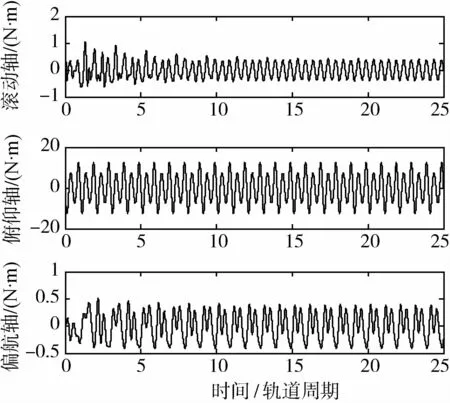
图5 CMG控制力矩

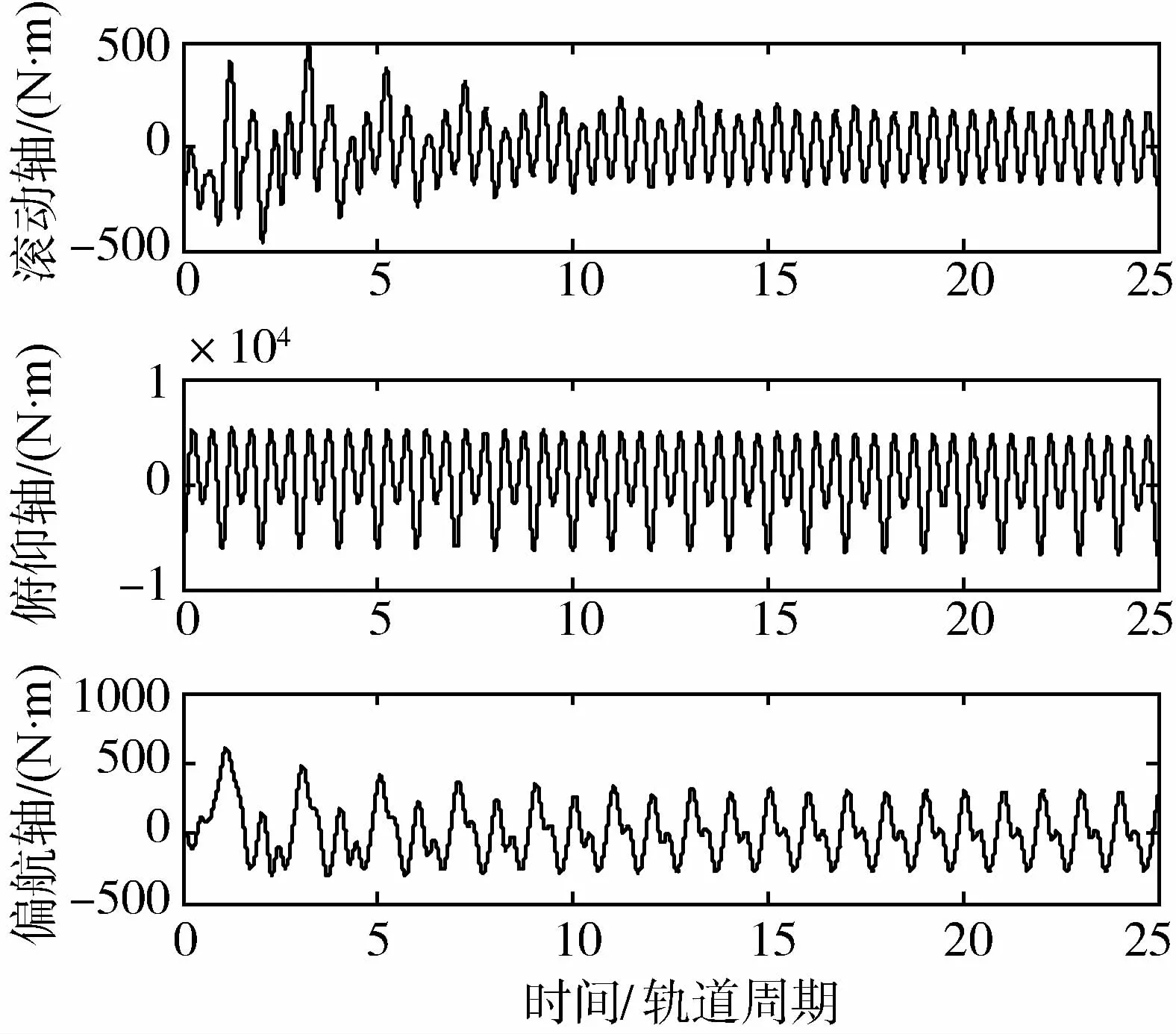
图6 CMG角动量

4 结论

针对空间站在惯性系内进行姿态保持时，由于重力梯度力矩常值部分以及气动力矩常值部分会引起角动量积累的问题，在惯性系内建立空间站动力学模型并线性化，利用滤波状态变量将系统状态扩维，采用LQR方法设计了惯性系内的角动量管理控制器，通过不同滤波导数矩阵的设计，可消除不同频率成份干扰对空间站姿态及控制力矩陀螺角动量的影响，达到角动量管理的目的，仿真验证了方法的有效性.仿真显示由于当前控制器只考虑了常值、单倍、双倍轨道频率成份的外干扰力矩，而惯性系内气动力矩的频率成份较多，特别三倍轨道频率成份幅值较大，而控制器设计中没有考虑该成份对姿态的影响，导致稳定后三轴姿态仍然有小幅值变化，将进一步分析空间站的重力梯度力矩、气动力矩的频率特性，改进控制器性能.

[1] Sayrchev V A, Legostaev V V, Sazonov M Y, et al. The passive attitude motion of the orbital stations Salyut-6 and Salyut-7[C]. IAF-87-355,the 38thInternational Astronautical Congress, Brighton,England, Oct.10-17,1987

[2] Harduvel J T. Continuous momentum management of earth-oriented spacecraft[J]. Journal of Guidance, Control, and Dynamics,1992, 15(6):1417-1426

[3] Branetz V N, Legostayev V P, Chertok B Y. The system of the Mir station motion control[C]. IAF-88-334,the 39thInternational Astronautical Congress, Bangalore, India,Oct.8-15,1988

[4] Warren W, Wie B, Geller D. Periodic-disturbance accommodating control of the space station for asymptotic momentum management[J]. Journal of Guidance, Control, and Dynamics, 1990, 13(6): 984-992

[5] Ryumin V V, Belyaev M Y. Problems of control arised during the implementation of scientific research program onboard the multipurpose orbital station[J]. Acta Astronautica, 1987, 15: 739-746

MomentumManagementControlofSpaceStationComplexinInertialReference

ZHANG Jun1,2, MA Yanhong1,2, HE Yingzi1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China；2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190,China)

For saturation of control moment gyros because of accumulation of constant component of gravitational torque and aero torque, a dynamics model of space station is established and linearized in inertial reference, then the state space equation is augmented by the filter states, and the linear quadratic regulator(LQR) method is used to design the feedback gain matrix for the momentum management controller of space station in inertial reference. In inertial reference the gravitational torque and aero dynamical torque are composed by multiples of frequency of orbit angular velocity, so the augmented filters can be selected according to the actual disturbance frequency to reduce the influence of different disturbing torgues on attitude of space station or momentum of control moment gyros, thus the space station can maintain attitude control without disaturation for long time. Simulation validats the controller.

space station; inertial reference; angular momentum management; control moment gyro