未知参数高阶线性系统基于特征模型的卡尔曼滤波*

2010-12-11龚宇莲吴宏鑫

空间控制技术与应用 2010年6期

关键词：适应控制卡尔曼滤波高阶

龚宇莲，吴宏鑫

(1.北京控制工程研究所,北京100190; 2. 空间智能控制技术重点实验室，北京100190)

未知参数高阶线性系统基于特征模型的卡尔曼滤波*

龚宇莲1,2，吴宏鑫1,2

(1.北京控制工程研究所,北京100190; 2. 空间智能控制技术重点实验室，北京100190)

针对一类有量测噪声的未知参数高阶线性系统设计了基于特征模型的卡尔曼滤波器，改进了由于传统卡尔曼滤波器在未知系统状态转移阵时应用的难题.在对高阶线性系统的自适应控制中，利用建立系统的特征模型构造状态转移阵，结合卡尔曼滤波的思想对系统输出进行滤波，使系统输出以及控制量的性能得到极大的改善.通过对一个未知参数的高阶线性系统仿真实验验证了此方法的有效性.

特征建模；黄金分割；自适应控制；卡尔曼滤波；高阶线性系统

自适应控制发展半个多世纪以来，提出了大量的自适应控制方法，基本的自适应控制的结构是由模型的辨识和控制律的设计两部分组成的.在高阶线性系统的自适应控制中，量测噪声一方面影响系统参数辨识的质量，另一方面噪声经控制器严重放大，导致控制输入性能恶化.文献[1]作者提出在有量测噪声时自适应控制对于控制量的要求不切实际的高.

因此要实现优良的控制，对信号在线滤波是必不可少的.针对参数已知，噪声符合高斯分布的情形，卡尔曼滤波已取得了很好的成果[2].但卡尔曼滤波器需要确知系统状态转移阵，因此在参数未知的系统中难以运用.文献[3]研究了系统参数含有不确定性时的滤波问题，提出了一种鲁棒滤波器，但并没有研究系统参数完全未知的情形.九十年代末，以序贯蒙特卡洛方法(SMC)为基础，发展出了粒子滤波器[4-5](PF).然而尽管PF在理论上，不要求知道系统的状态方程，只需要系统状态量的先验概率密度函数或构造一个重要性采样函数，但在系统参数未知时概率密度函数难以获得，重要性采样函数的选取也没有很好的方法，因此其应用也具有很大局限.目前，除了简单的低通滤波器(LPF)外，针对系统参数未知情形下量测噪声的滤波问题的研究仍然较为缺失.

本文针对系统参数未知的高阶线性系统有量测噪声情况下自适应控制性能恶化的问题，利用特征模型对系统输入输出的低阶建模，结合卡尔曼滤波的思想，设计出基于特征模型的卡尔曼滤波器(CKF).本文第1部分对问题进行描述并介绍预备知识；第2部分设计基于特征模型的卡尔曼滤波器；第3部分仿真验证；最后总结该滤波方法的优势以及局限性.

1 问题描述及预备知识

1.1问题的描述

考虑一类有量测噪声的未知参数高阶线性系统：

其中，u为控制量，x为系统输出，y为带白噪声e的量测值.

对系统(1)这类高阶线性系统的跟踪问题，在无噪声情况下，基于特征模型的黄金分割自适应控制律[6-8]已经可以很好地解决，文献[8]对于特征模型理论作了系统而详尽的阐述，并列举了大量工程应用实例.但在量测噪声存在的情况，计算控制量所用到的反馈信号来源于有量测噪声的测量值，因而计算得到的控制量会随着带噪声信号剧烈变化.文献[1]作者研究大型挠性航天器有量测噪声情况下的自适应控制时，用仿真显示了控制量剧烈抖动的情形.而目前大部份研究有量测噪声情况下控制问题的论文中，作者都避免提及控制量的情形.因此，本文主要考虑如何通过对这类系统的量测值进行滤波，从而设计出较为平稳的控制量.

1.2卡尔曼滤波器

卡尔曼滤波方法[2]自上世纪中期提出以来，因其在解决有噪声情况下的实时最优估计问题上的优势，立即受到了工程界的重视.对于如下用状态方程描述的线性系统：

如果系统状态噪声w(k)、量测噪声v(k)符合零均值高斯分布，则系统状态量的最优卡尔曼滤波器为：

卡尔曼滤波增益阵K(k)由下式递推得到：

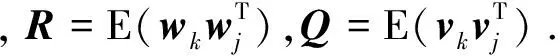
几十年来，卡尔曼滤波的研究逐渐深入，然而现有的各种改进的卡尔曼滤波方法都要求已知系统的状态转移阵.在未知系统状态转移阵时，如果可以得知系统的阶数，用辨识方法得到其系统参数，再利用辨识出的参数设计高阶的卡尔曼滤波器，在理论上是一种解决方法.但是参数辨识以及计算卡尔曼滤波增益阵的时间复杂度都是R(n2).事实上，即使在系统参数已知的情况下，系统阶数较高时，过高的计算量也影响了卡尔曼滤波器的应用.因此，如果可以将高阶系统用低阶状态转移方程描述，并以低阶状态转移方程设计卡尔曼滤波器，将会为高阶系统的实时滤波提供很好的解决途径.

1.3高阶线性系统的特征建模

对于高阶线性系统的低阶建模问题，特征建模理论[6-8]提供了很好的解决办法.所谓特征建模，就是根据对象动力学特征、环境特征和控制性能要求相结合进行建模，而不仅以对象精确的动力学分析来建模，特征模型的特点如下：

(1)在同样输入控制作用下，对象特征模型和实际对象在输出上是等价的(即在动态过程中能保持在允许的输出误差内)，在稳定情况下，输出是相等的.

(2)特征模型的形式和阶次除考虑对象特征外，主要取决于控制性能要求.

(3)特征模型建立的形式应比原对象的动力学方程简单，易于控制器设计，工程实现容易、方便.

(4)特征模型与高阶系统的降阶模型不同，它是把高阶模型有关信息压缩到几个特征参量之中，并不丢失信息，一般情况下特征模型用慢时变差分方程描述.

文献[6]提出将高阶线性系统化为二阶时变差分方程的特征模型形式，并提出了黄金分割控制器，文献[7]进一步证明，对于式(5)中的高阶线性系统：

采样时间足够小的情况下，其特征模型可以描述为式(6)的慢时变二阶差分方程形式：

x(k+1)=f1(k)x(k)+f2(k)x(k-1)+

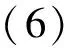
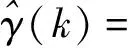
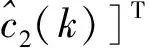
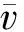
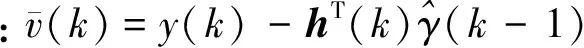
递推辨识方程如下：

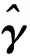
D(k)=R(k-1)h(k)[hT(k)R(k-1)h(k)+λ]-1,

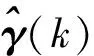
2 控制器设计

对于式(1)中的系统，根据特征建模理论，可以描述为如下的带量测噪声的二阶时变差分方程形式：

将其特征模型化成状态空间的形式：

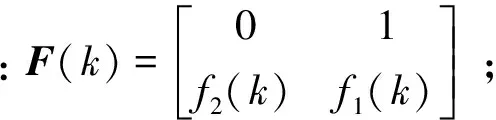
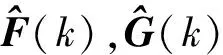
其中：

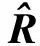
P(k)=[I-K(k)C(k)]P(k|k-1)[I-K(k)

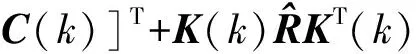
将此滤波方案结合黄金分割控制器[6]，构成自适应控制方案，其控制器结构为图1所示.

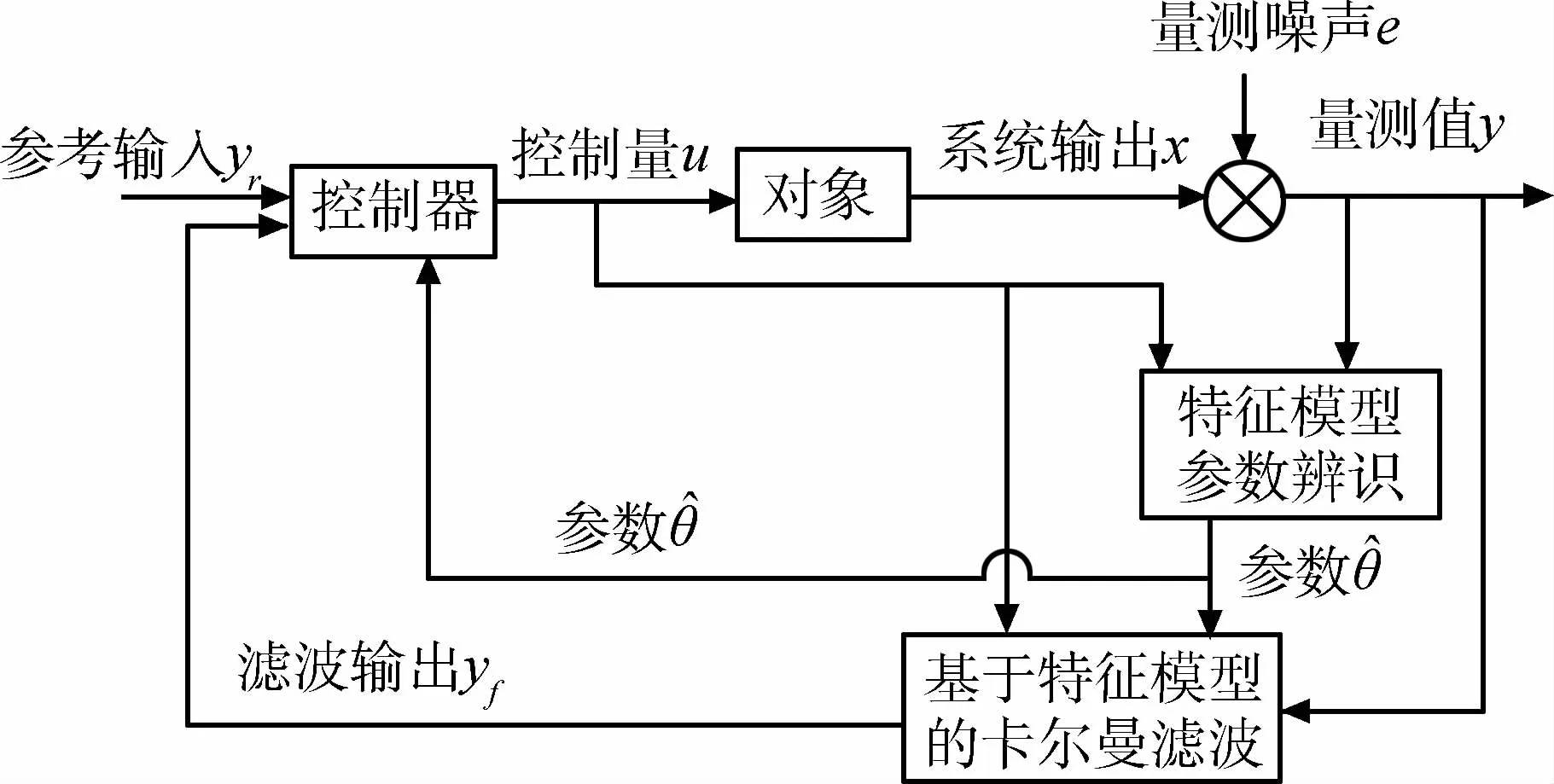
图1 基于特征模型的卡尔曼滤波器

在应用中，量测噪声序列的方差阵可以根据量测装置的统计特性得知，系统噪声包含辨识参数的误差造成的系统偏差，其大小很难得知，应用中可先设定一个较小的值.

3 仿真实验

带量测噪声的高阶线性系统：

其中：

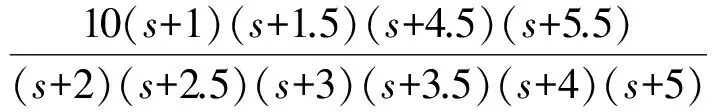
系统(12)为一个高阶线性系统.因此在采样时间足够小时，特征建模理论是成立的.设计控制器，将系统从0跟踪到10.假设系统的量测噪声e符合N(0,1)的正态分布.

采用式(9)中的辨识方法，构建图1中的控制系统进行仿真.控制律采用基于特征模型的黄金分割控制律结合维持跟踪和逻辑积分控制[6]：

黄金分割控制律：

ul(k)=

维持跟踪控制律：

u0(k)=

逻辑积分控制律：

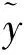
(19)

总的控制量:

(20)

其中：

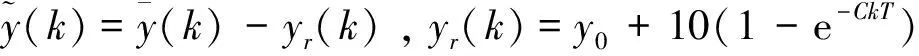
仿真实验中分别在不进行滤波、应用数字低通滤波器(LPF)以及应用基于特征模型的卡尔曼滤波器(CKF)的情况下进行实验.仿真时间100s，采样时间0.01s.考虑到过渡段低通滤波器对信号的跟踪能力较弱，而基于特征模型的卡尔曼滤波器也需要一定的时间获取系统特征模型的参数辨识值，因此在仿真前2s，都不使用滤波信号.3种情况下控制系统仿真实验的系统输出真值、量测信号、以及控制量的变化曲线分别为图2～4.

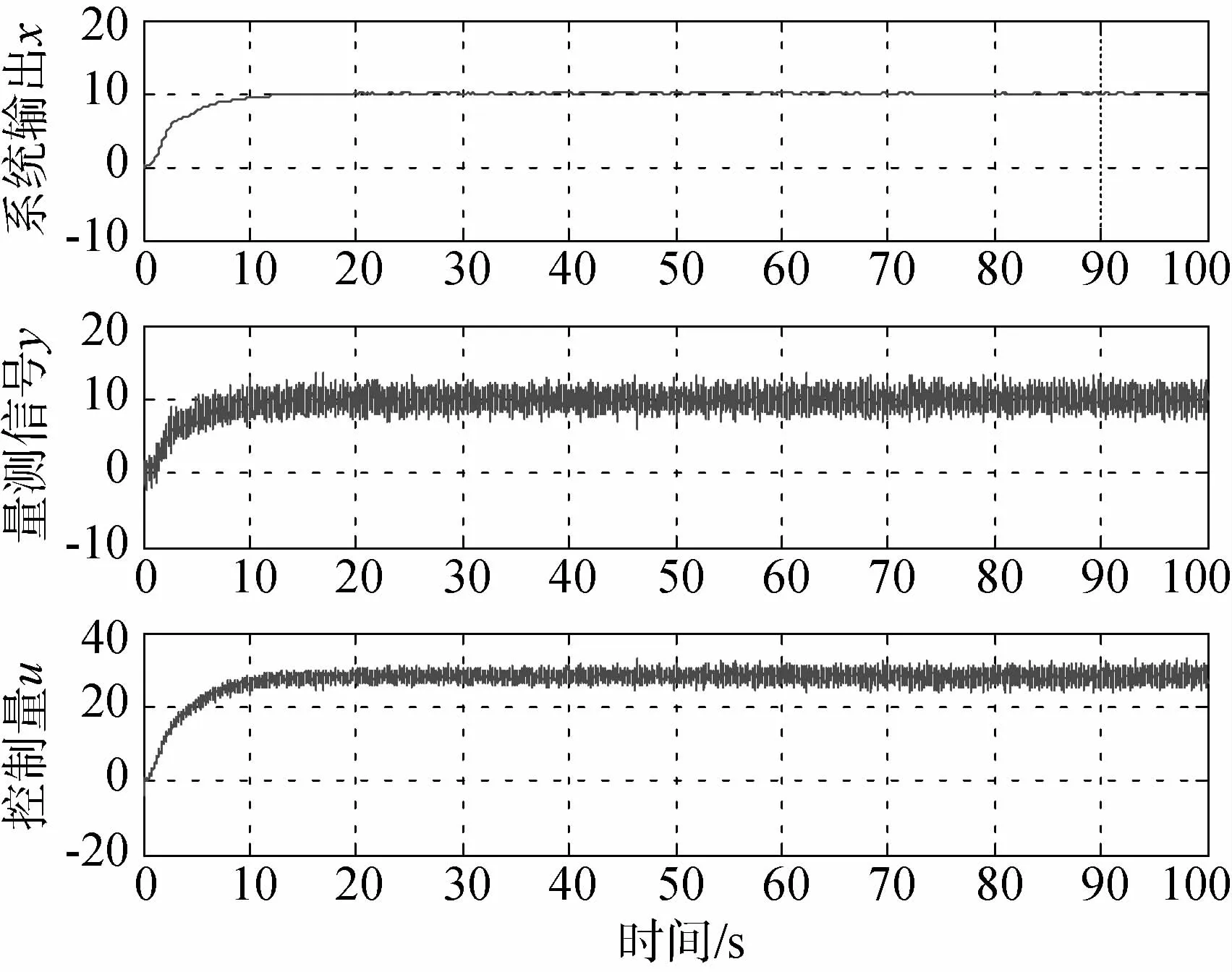
图2 无滤波控制仿真

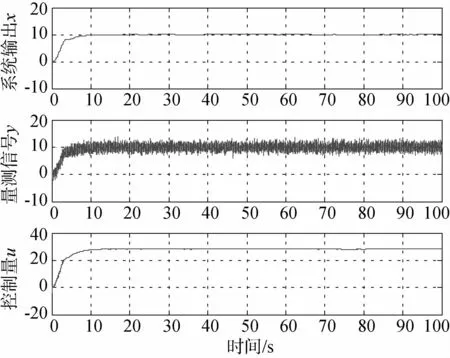
图3 LPF滤波控制仿真

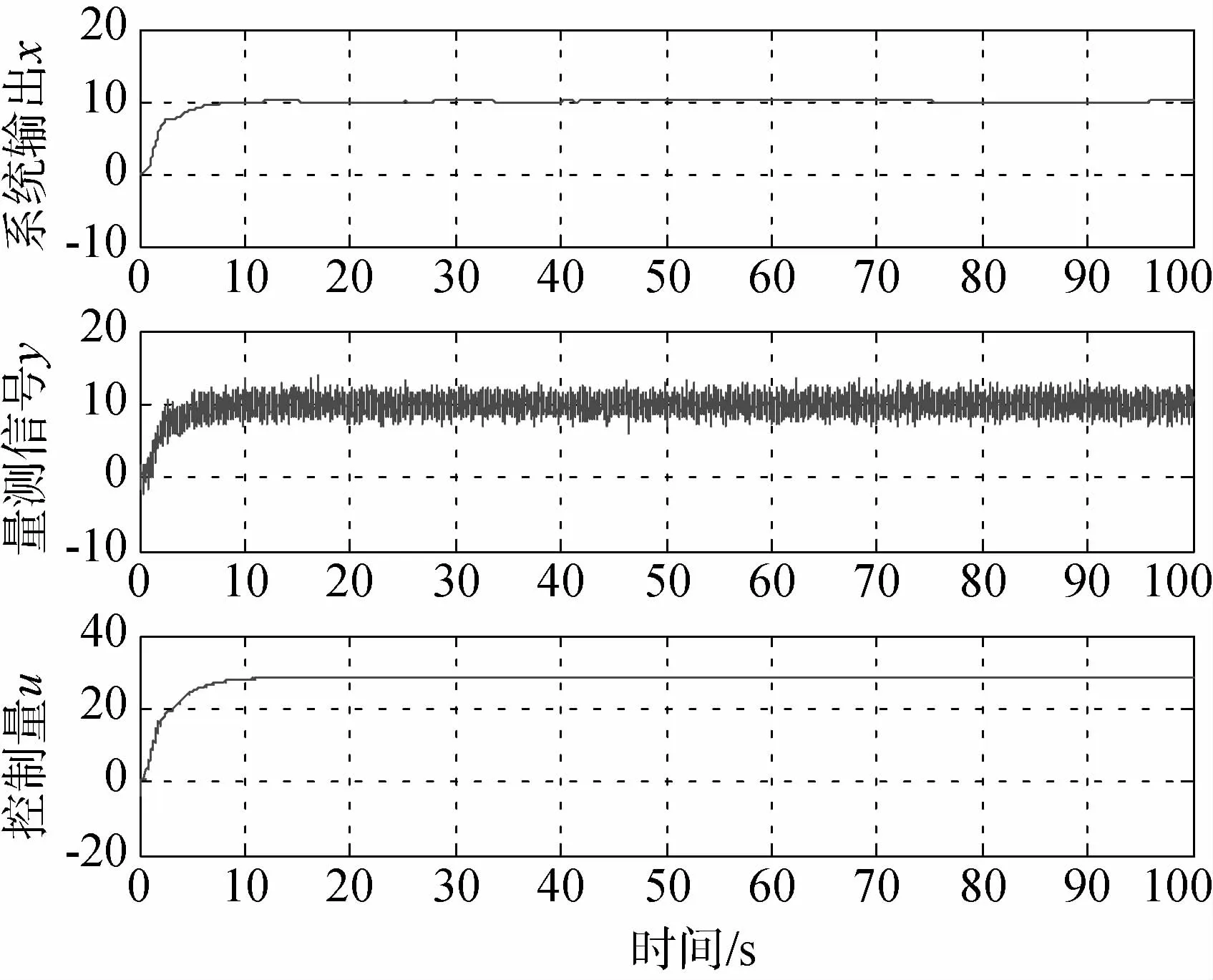
图4 CKF滤波控制仿真

图5针对稳态时系统变化较小，将坐标放大，观察3个方案的稳态性能.3个实验在稳态阶段(20s～100s)的系统输出以及控制输入的均值、方差由表(1)中列出.

图6、图7给出应用低通滤波器(LPF)和基于特征模型的卡尔曼滤波器(CKF)实验中过渡段(0～10s)，CKF和LPF的滤波情况.

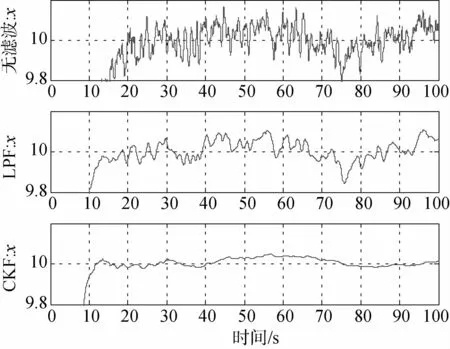
图5 3种方案稳态输出细节

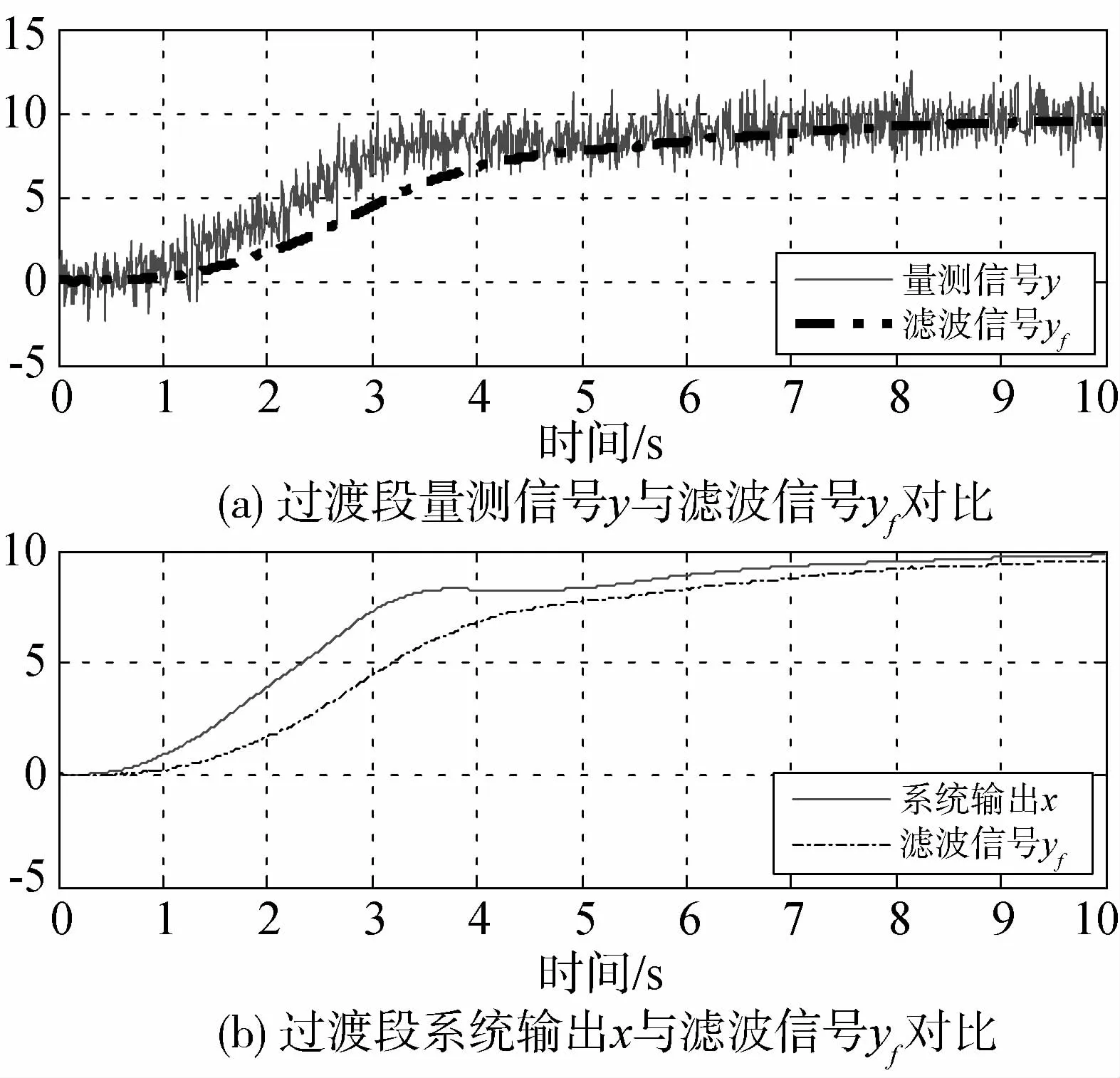
图6 LPF过渡段滤波情况

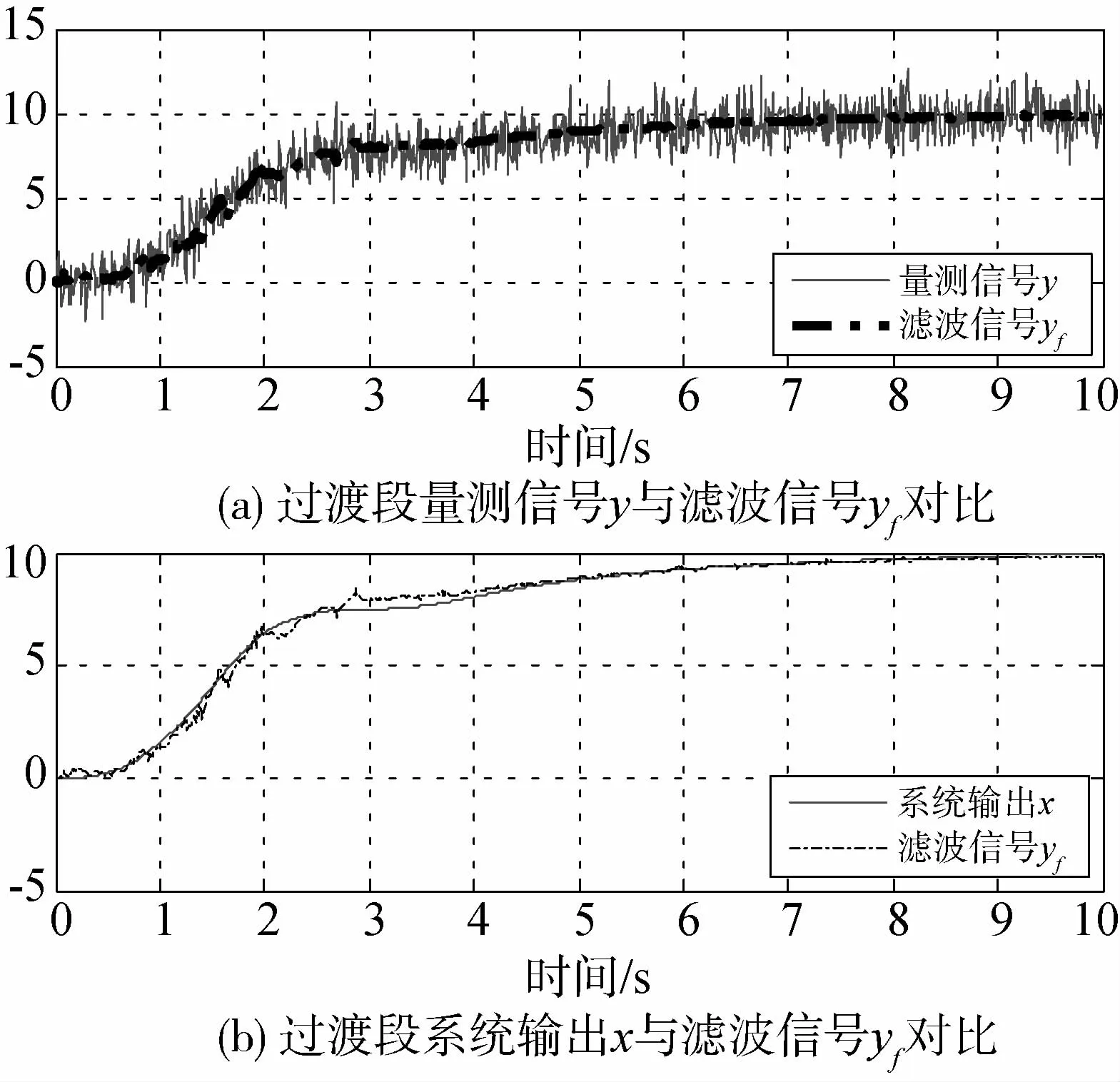
图7 CKF过渡段滤波情况

图8为LPF和CKF在稳态阶段(20～100s)各自的系统输出真值与控制量坐标放大的变化曲线.图9列出了整个控制过程中，两种滤波器滤波信号与系统真实输出信号的偏差变化曲线.

从仿真图以及表1的数据可以看出，基于特征模型的黄金分割控制器即使不经滤波也可以保证较高的系统输出精度，但不经滤波的情况下，控制量的性能恶化，控制量输入的均方根达到1.27,实际信号大约在均值的正负三倍均方根内变化(如图2所示).控制量的剧烈变化对执行机构要求过高，甚至根本无法实现.

对比两种滤波方案，在系统过渡段，由于LPF是靠抑制信号带宽实现对高频干扰的滤波，因此LPF对信号的变化敏感性较弱，实验中可以看出在系统过渡过段LPF的滤波信号与真值的偏差较大，如果继续降低带宽，偏差会继续增大，从而严重影响系统动态性能.

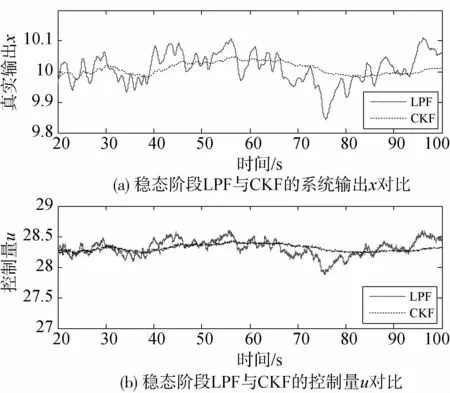
图8 稳态阶段两种滤波器对比

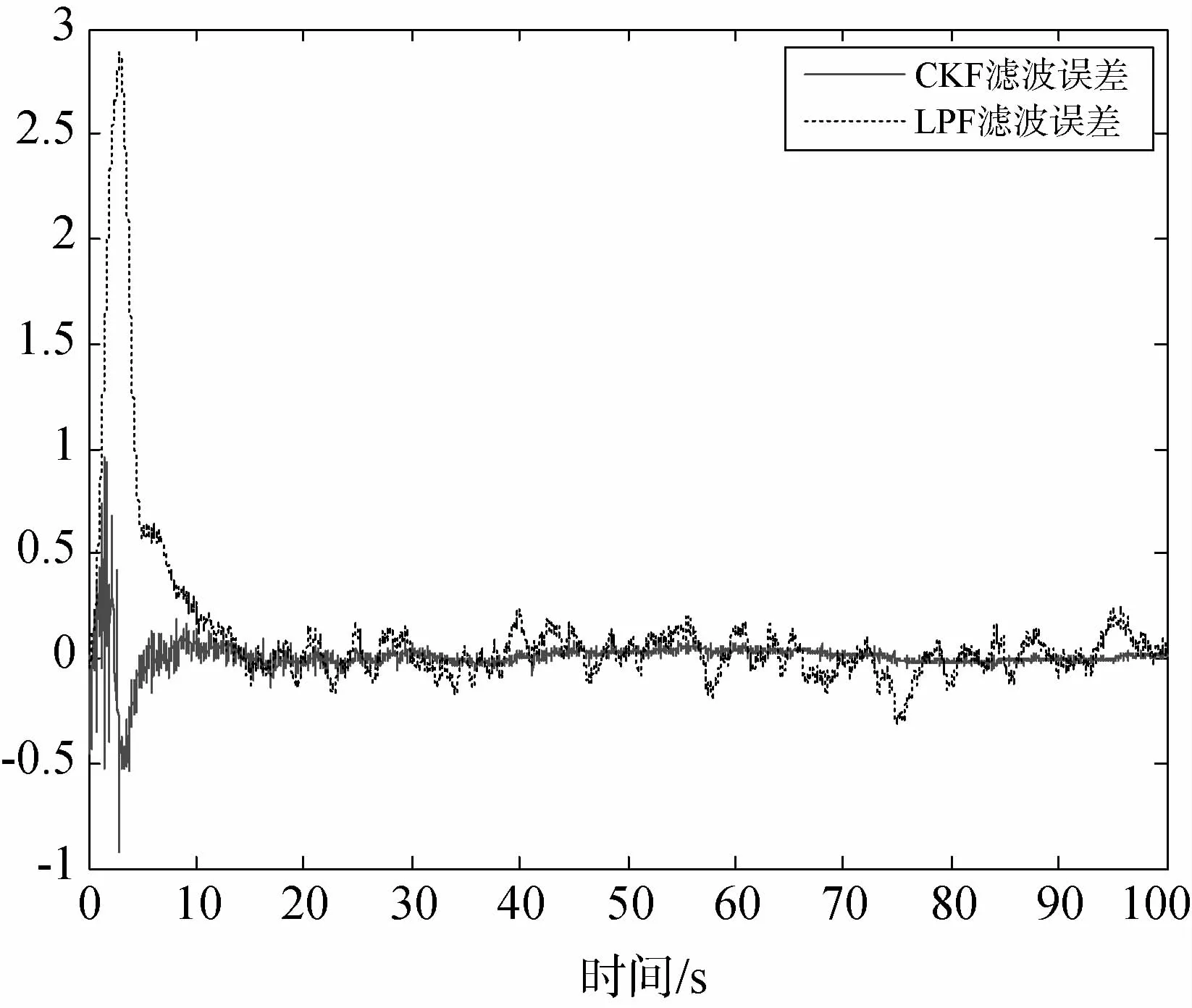
图9 全过程滤波误差情况

从图8以及表1中的数据可以看出稳态阶段用CKF滤波的系统输出以及控制量输入都比LPF要平稳.图9全过程滤波误差显示出，基于特征模型的卡尔曼滤波器(CKF)无论过渡段还是稳态阶段，滤波性能都优于简单的低通滤波(LPF).由于平稳的滤波信号，使系统的自适应控制输入输出性能得到大大改善.

4 结论

本文试图通过对带噪声的量测信号滤波，以改善在有量测噪声情况下的自适应控制性能恶化的问题.由于卡尔曼滤波器必需知道系统状态转移阵的局限性，本文针对线性系统参数未知情况，通过辨识系统特征模型参数构造二阶的状态转移阵，探索了一种解决方案.同时，由于使用低阶的特征模型，使得卡尔曼滤波器在高阶系统中面临的计算量过大问题得到改善.

由于本方法是基于特征模型而设计滤波器，需要特征模型的辨识参数构造状态转移阵,因此在特征建模理论不成立的情况下，还有待进一步研究.

[1] Bayard D S, Ih C C, Wang S J. Adaptive control for flexible space structures with measurement noise[C]. Control Conference, American, June 15-16, 1982

[2] 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社, 1998

[3] Wu Z, Shi H, Liu B S. INS/GPS integrated navigation uncertain system state estimation based on minimal variance robust filtering[C]. IMACS Multi conference on “Computational Engineering in Systems Applications” (CESA), Beijing, China, October 4-6, 2006

[4] 程水英，张剑云. 粒子滤波评述[J]. 宇航学报，2008, 29(4):1099-1111

[5] Arulampalam M S, Maskell S, Gordon N, et al. A tutorial on particle filters for online nonlinear/non-gaussian Bayesian tracking [J]. IEEE Transactions on Signal Processing, 2002, 50(2):174-188

[6] 吴宏鑫，刘一武，刘忠汉，等.特征建模与挠性结构的控制[J].中国科学(E辑),2001,31(2):137-149

[7] 孟斌，吴宏鑫.线性定常系统特征模型的证明[J].中国科学(E辑)，2007,37(10):1258-1271

[8] 吴宏鑫，胡军，解永春.基于特征模型的智能自适应控制[M]. 北京:中国科学技术出版社,2009

CharacteristicModel-BasedKalmanFilterfortheHighDimensionLinearSystemswithUnknownParameters

GONG Yulian1,2, WU Hongxin1,2

(1.BeijingInstituteofControlEngineering,Beijing100190，China; 2.ScienceandTechnologyonSpaceIntelligentControlLaboratory，Beijing100190，China)

In this paper, a characteristic model based Kalman filter (CKF) is designed for high dimension linear systems with unknown parameters. The proposed approach overcomes difficuties in the application of traditional Kalman filters in unknown parameter systems. By building the characteristic model of the high dimension system, a state transfer matrix is constituted， and the CKF is establishedin combination with the algorithm of Kalman Filter. The CKF is used to filter the output signal with measurement noise, the performance of the adaptive control of high dimension systems is improved, and simulation results prove the capability of this method.

characteristic model; gold section; adaptive control; Kalman filter; high dimension linear system