航天器姿态指向跟踪的一种自适应滑模控制方法

2010-12-11王冬霞贾英宏周付根

空间控制技术与应用 2010年6期

关键词：角速度滑模指向

王冬霞, 石恒, 贾英宏, 周付根

(北京航空航天大学，北京 100191)

航天器姿态指向跟踪的一种自适应滑模控制方法

王冬霞, 石恒, 贾英宏, 周付根

(北京航空航天大学，北京 100191)

航天器姿态指向跟踪(APT)技术是近年来引起深入研究的关键技术之一，设计一种自适应滑模控制律，通过设计自适应律考虑有界干扰力矩和转动惯量不确定因素的影响，同时使用滑模控制设计方法保证控制算法的鲁棒性，用双曲正切函数代替符号函数来克服滑模控制中存在的抖振问题，实现受控航天器的某个指向(相机或天线)保持对运动目标的跟踪.控制方案采用修正罗德里格斯参数(MRP)描述航天器姿态，用喷气推力器作为航天器的姿态执行机构.仿真结果显示了控制律的有效性.

姿态指向跟踪；自适应滑模控制；修正罗德里格斯参数

近年来，航天器姿态指向跟踪(APT)技术研究成果广泛应用于移动目标跟踪、区域监视、空间中继通信、海洋环境监测以及天基扫描成像等领域.指向跟踪规律确定和复杂条件下的姿态控制是APT技术实现的两大关键环节.跟踪指向规律确定属运动学问题，本文重点关注后者，围绕星载载荷的高精度指向保持，展开复杂条件下的姿态指向跟踪控制问题研究.

姿态指向跟踪控制问题可归结为不确定扰动条件下的大范围非线性控制问题.充分考虑各种扰动因素，采用适当控制方法设计高性能的姿态控制律，保持控制系统的稳定性和良好的动态性能是实现姿态指向跟踪控制的关键.文献[1-2]用非线性H∞控制和backstepping设计法处理姿态控制问题，但没有考虑航天器的惯量不确定性；文献[3]采用欧拉角设计滑模控制律，但由于欧拉角在大角度时存在奇异性，限制了该方法的应用范围；文献[4-5]采用四元数设计姿态控制律，但由于四元数有一个冗余参数，致使控制器的物理意义不明确；文献[6-8]研究了如何克服滑模控制方法中的抖振现象，其中[6]将不连续的控制信号连续化，[7-8]分别采用饱和函数与近似符号函数代替变结构控制常用的符号函数；文献[9]控制律可以估计系统的不确定性，消除传统滑模控制中对不确定界的要求.

以上述讨论为出发点，本文针对转动惯量不确定设计自适应律，保证趋近模态渐近收敛.进而使用鲁棒性较强的滑模控制方法得出姿态控制律，保证任意初始状态都可以在有限的时间内收敛到滑动平面，并用双曲正切函数代替符号函数来克服滑模控制中存在的抖振问题.采用这种控制器无需知道航天器的惯量及其不确定性的上下界，通过控制器中的自适应律来自动适应航天器惯量的不确定性，保证了良好的鲁棒性.

1 数学模型

1.1坐标系的定义

为描述航天器的姿态指向跟踪问题，引入如下坐标系：

1)惯性坐标系Si：原点为地心，Xi轴指向春分点，Zi轴为地球自转轴，Yi轴与Xi，Zi轴构成右手坐标系.

2)星体坐标系Sb：原点为主星质心，三轴固连于星体上，分别与星体的惯量主轴方向一致.

3)视线坐标系Ss：原点为主航天器质心；Xs轴指向目标航天器质心；Ys轴为Xs轴与Xb轴的叉乘方向；Zs轴由右手定则得到.若在某时刻相对运动中Xs轴与Xb轴重合，此时上述基于叉乘的定义无效，直接令Ys轴、Zs轴分别与Yb轴、Zb轴重合.

1.2航天器的姿态动力学方程

航天器的姿态动力学方程又称为欧拉转动方程，描述的是角速度矢量在外力矩作用下随时间的变化规律，如果只考虑控制力矩和干扰力矩，并且它们与星体坐标系固连，则姿态动力学方程可以表示为[10]

式中，ω表示航天器本体坐标系相对于惯性系的角速度，J表示航天器的转动惯量，Tc表示作用于航天器质心的外力矩，Td表示未知的干扰力矩，不妨假设它是有界的.ω×表示叉乘运算的反对称矩阵[11].

1.3航天器的姿态运动学方程

姿态运动学方程建立了姿态参数的导数与角速度的关系，不同的姿态描述参数对应的运动学方程的形式亦不相同，选取MRP参数描述航天器的姿态，相应的运动学方程为[11]

式中，

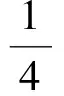
2 姿态指向跟踪问题的数学描述

2.1任务描述

在空间飞行器监视，以及接近交会过程中的载荷指向跟踪是APT技术的典型应用.实现大范围相对运动的两航天器间的载荷指向跟踪，需考虑机动历程内目标航天器相对于主航天器的实时运动，此时的机动终端位置是一个与目标机动轨迹有关的时变向量函数，因此本文以主航天器至目标航天器的相对指向矢量为基础，定义视线坐标系，确立主航天器的指向跟踪姿态基准.

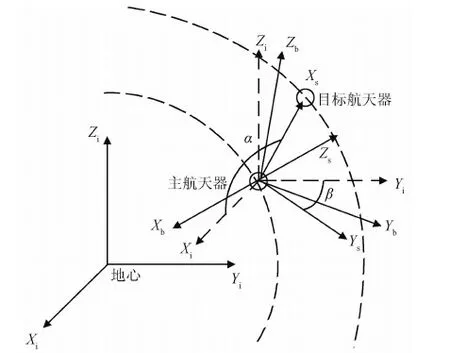
图1 任务坐标系之间的几何关系

如图1所示，假定相机等跟踪载荷与主航天器固连安装，安装位置与主航天器质心重合，载荷跟踪视线方向与Xb轴重合，则只要使Sb系与Ss系重合，就达到了姿态跟踪机动的目标.设Xs轴到Xi轴的夹角为α，Ys轴到Yi轴的夹角为β.α和β的值取决于两航天器的轨道运动，由导航系统实时给出.根据Ss的定义和MRP的转动合成关系，由下面两式定义σd和ωd，分别表示Si相对于Ss的MRP和角速度在Si中的投影：

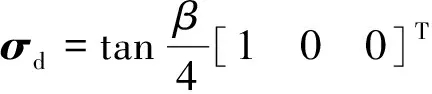
式(3)中，⊗为MRP乘法，因此由式(3)计算的σd表示如下的转动，即首先绕Ys轴转动α，再绕Xs转动β.式(4)中，Cis是由Si相对于Ss的MRP参数σd计算而得的方向余弦矩阵[12].

定义δσ为Sb相对于Ss的MRP，δω为Sb相对于Ss的角速度矢量在Sb中的投影.δσ和δω代表Sb相对于Ss的姿态状态，即姿态误差信息.定义σ为Sb相对于Si的MRP，ω为Sb相对于Si的角速度矢量在Sb中的投影，则有

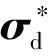
2.2姿态跟踪误差系统的描述

根据式(2)可知姿态指向跟踪误差的运动学方程为

对式(6)求导并代入式(1),姿态指向跟踪误差的动力学方程为

由上述问题描述可知，航天器姿态指向跟踪控制问题的目标是：对于系统(7)、(8)，设计控制律，使得δσ→0,δω→0.

3 控制律的设计

3.1滑模控制律的设计

取滑动平面为

及趋近律为

式中ε=diag{ε1， ε2， ε3}，εi是正数，sgn(s)=[sgn(s1) sgn(s2) sgn(s3)]T，对式(9)求导，并利用式(7)和(8)得：

代入式(10)得：

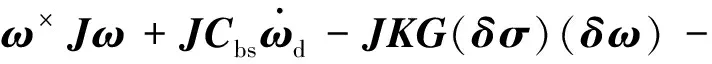
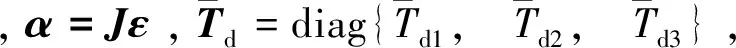
式(11)中采用了符号函数，符号函数的存在使得Tc不连续，在稳态时会有抖振存在.为了减小稳态时的抖振，用双曲正切函数 th (s/p2)来代替符号函数sgn(s)，即用平滑函数代替不连续函数，其中p为转移因子，为了保证函数 th (s/p2)接近sgn(s)，p应取较小的值.因此控制律为：

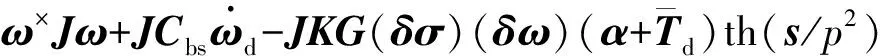
3.2自适应控制律的设计

实际上，航天器的转动惯量是未知或变化的，所以不能直接利用控制律(12)，下面引入自适应控制律，用于模型参数不确定情况.

对于惯量矩阵J：

定义算子L为：

L(J)=[J11J12J13J22J23J33]T，

任意给定三维矢量a=[a1a2a3]T和b=[b1b2b3]T，使得算子h满足：

aTJb=LT(J)h(a,b)，

即可定义算子h为：

h(a,b)=[a1b1a1b2+a2b1a1b3+a3b1

a2b2a2b3+a3b2a3b3]T.

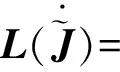
(13)

使用转动惯量的估计值代替真值，指令控制力矩为

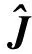
(14)

为分析(13)和(14)的稳定性，考虑Lyapunov函数：

对Lyapunov函数求导，并代入式(13)和(14)得：

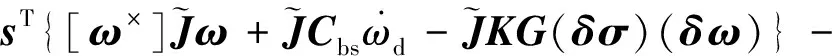
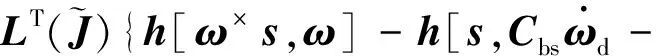
KG(δσ)(δω)]}

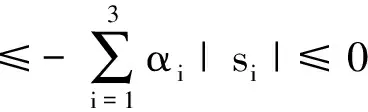
当且仅当s=0时，最后一步的等号成立.根据Lyapunov稳定性理论，当t→∞时，s→0，即系统将从任意初始状态收敛到滑动平面上.根据Lasalle不变集原理[13]可知，当s→0时，δσ→0,δω→0，即达到控制目标.

4 仿真结果及分析

仿真验证中不可能对任意初始状态和控制指令进行数值仿真，这里基于典型的航天器间跟踪指向任务，由相对导航计算得到主航天器跟踪指向的姿态与姿态角速度指令，如图2、图3所示.

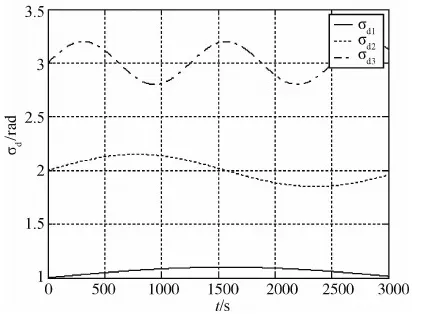
图2 目标指令姿态角

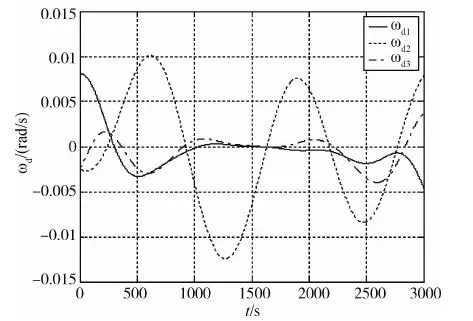
图3 目标指令姿态角速度

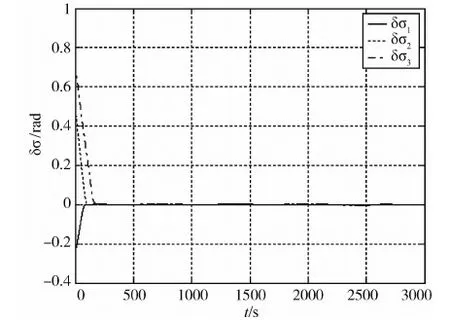
图4 姿态角误差图(文献[9])

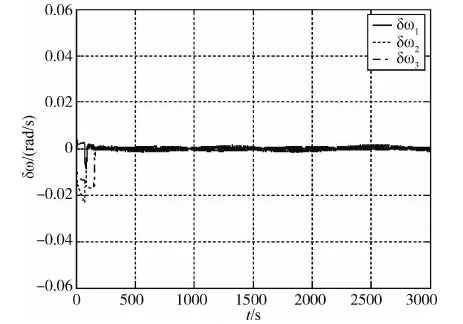
图5 姿态角速度误差图(文献[9])

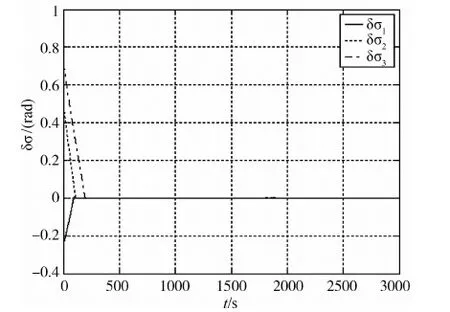
图6 姿态角误差图

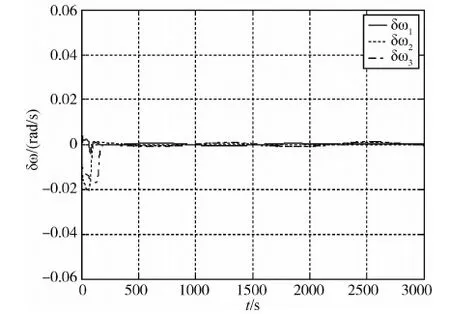
图7 姿态角速度误差图

将文献[9]的控制律与本文的控制律相对比，可以看出本文对抖振有更好的抑制能力.

图6及图7表明：该姿态控制律能够在200s内完成对运动的目标的指向，并保持长期的后续指向跟踪.仿真设定的3000s跟踪段内，姿态角及姿态角速度与目标姿态角及姿态角速度的吻合程度均比较好.

5 结论

本文针对复杂条件下的姿态指向跟踪控制问题，即实现受控航天器的某个指向(相机或天线)保持对运动目标的跟踪问题，设计了自适应滑模控制律.姿态描述模型中采用MRP参数，这种参数无参数冗余、在[0°, 360°]范围内奇异性容易通过参数切换避免，而且该参数便于建立运动学模型，便于设计控制器；考虑有界干扰力矩，使用鲁棒性较强的滑模控制方法研究了姿态指向跟踪问题，设计的滑模控制律使得任意初始状态都可以在有限的时间内收敛到滑动平面，针对滑模控制中存在的抖振问题，用双曲正切函数代替符号函数来克服；对于转动惯量未知或慢变的情形，设计了自校正控制律，并且分析了趋近模态的收敛性.仿真结果验证了该控制律的有效可行.

[1] Show L L, Juang J C, Jan Y W. An LMI-based nonlinear attitude control approach [J]. IEEE Transactions on Control Systems Technology, 2003, 11 (1):73-83

[2] Kristiansen, Nicklasson P J . Satellite attitude control by quaternion-based backstepping[C].American Control Conference, Portland , 2005

[3] 胡庆雷,马广富.带有输入非线性的挠性航天器姿态机动变结构控制[J]. 宇航学报，2006，27(4):630-634

[4] 袁长清, 李俊峰, 宝音贺西. 多体航天器姿态跟踪终端滑模控制[C]. 全国第十三届空间及运动体控制技术学术会议,湖北宜昌，2008

[5] 冯璐,龚诚,何长安. 一种基于误差四元数的飞行器姿态跟踪系统的滑模控制器[J]. 宇航学报, 2000, 21(1): 17-22

[6] Liu X J, Guan P, Liu J Z. Fuzzy sliding-mode control of satellite[C].Decision and Control and European Control Conference, Seville, 2005

[7] Hyochoong B. Sliding mode control for spacecraft containing rotating wheels[C].AIAA Guidance, Navigation, and Control Conference and Exhibit, Montreal, 2001

[8] Jovan D B, L I SM. Robust adaptive variable structure control of spacecraft under control input saturation [J]. Journal of Guidance, Control and Dynamics, 2001, 24(1): 14-22

[9] 卜邵华，宋斌. 航天器姿态跟踪系统的自适应滑模控制 [J]. 控制工程，2008, 15: 38-41

[10] Sidi M J. Spacecraft dynamics and control[M]. Cambridge: Cambridge University Press, 1997

[11] Tsiotras P. Stabilization and optimality results for the attitude control problem[J]. Journal of Guidance, Control, and Dynamics, 1996, 19 (4): 772-779

[12] 肖业伦. 航天器飞行动力学原理[M]. 北京：宇航出版社,2003

[13] Khalil H K. Nonlinear system [M]. New York: Macmillan, 1992

AdaptiveSliding-ModeControlforSpacecraftAttitudePointingandTrackingSystem

WANG Dongxia, SHI Heng , JIA Yinghong , ZHOU Fugen

(BeijingUniversityofAeronauticsandAstronautics,Beijing100191,China)

Spacecraft attitude pointing and tracking (APT) is one of key techniques to be lucubrated recently. This article is aimed to design a kind of adaptive sliding mode control law. Considering effects of some uncertain factors such as bounded disturbing torque and rotational inertia,the adaptive law scheme is designed. At the same time, a sliding mode control method is used to guarantee the robustness of control algorithm and it uses hyperbolic tangent function, instead of sign function, to avoid the buffet existed in sliding mode control, thus keeping a specific poiniting of controlled spacecraft tracking some moving object. In the control method, the modified Rodrigues parameter (MRP) is used to describe spacecraft attitude, and a jet thruster as the actuator. Simulation result shows the effectiveness of this control law.

attitude pointing and tracking; adaptive sliding-mode control; modified Rodrigues parameter