基于自适应观测器的飞轮故障诊断物理仿真*

2010-12-11田科丰李明航

空间控制技术与应用 2010年6期

关键词：飞轮观测器增益

田科丰,李明航

(1.北京控制工程研究所,北京 100190;2.空间智能控制技术重点实验室,北京 100190;3.厦门大学自动化系, 厦门 361005)

基于自适应观测器的飞轮故障诊断物理仿真*

田科丰1,2,李明航3

(1.北京控制工程研究所,北京 100190;2.空间智能控制技术重点实验室,北京 100190;3.厦门大学自动化系, 厦门 361005)

研究了反作用飞轮的故障诊断问题.针对反作用飞轮的非线性数学模型，分析了其故障模式，建立了其故障的参数化描述方法，并在此基础上提出了一种基于参数自适应投影的反作用飞轮故障诊断方法.该方法通过构造观测器，利用参数自适应投影算法来更新参数信息，保证观测器的误差收敛到零.最后对飞轮的正常模式和3种故障模式进行了物理仿真实验，结果表明提出的方法有效可行.

故障诊断；自适应投影算法；故障模式；反作用飞轮；物理仿真

反作用飞轮是航天器姿态控制系统中的惯性执行部件，也是航天器长期轨道运行模式中，姿控分系统的主要执行部件.采用飞轮进行航天器姿态控制所依据的原理是角动量守恒.根据角动量守恒原理，当卫星不受外力矩作用时，航天器连同轮系的角动量将保持恒定，所以轮系角动量的变化(大小与方向)必将引起卫星本体角动量的反向变化.在航天器姿控系统中，飞轮将按照姿控系统指令，输出相应的控制力矩，校正航天器的姿态误差，或完成姿态的调整.

飞轮带有机械转动部件，在长时间工作过程中，由于连续作机械运动，很容易发生故障，无法完成要求的执行任务[1].虽然由于硬件上的改进，已经大大提高了飞轮的可靠性和使用寿命，但相对于控制系统其他部件而言，轮控系统的故障率仍然较高.若不能及时检测并排除故障，可能会导致卫星姿态失控.飞轮的主要故障有空转、停转、摩擦力矩增大、飞轮增益效率下降等，故障原因与切换飞轮的驱动器和脉冲时钟失效、飞轮绕组开路或短路或缺少润滑剂有关.

文献[2]在最小二乘参数估计方法的基础上提出了全最小二乘参数估计的递推形式，证明了飞轮参数估计的收敛性，并应用到了飞轮缓变故障的检测和诊断上.文献[3]针对飞轮故障系统，建立了一种自适应观测器，通过在线调整来在线逼近故障后执行器的未知参数.本文将针对反作用飞轮的数学模型，通过构造自适应观测器来辨识与飞轮故障相关的参数.观测器将只利用飞轮的输入输出信息进行参数的更新，与文献[3]基于全局的观测器相比，本方法具有更快的收敛速度.

1 问题描述

1.1反作用飞轮数学模型

在反作用飞轮的工作区间内，其数学模型[4]可表示为

1.2飞轮故障模式及其参数化描述

反作用飞轮的主要故障模式有空转、停转、摩擦力矩增大和飞轮效率下降等4种.饱和是飞轮一个不可避免的缺点，大多数情况下不归为故障[1].飞轮的故障模式大致有以下几种：

a. 空转.飞轮不能响应正常的控制力矩指令，飞轮的转速几乎维持不变(在摩擦力的作用下缓慢减小)，输出力矩几乎为零；

b. 停转. 输出力矩首先产生一个巨大的反向扰动，然后快速变为零；

c. 摩擦力矩增大.主要原因包括轴承温度增高、轴承润滑不好等，摩擦力矩增大将导致飞轮输出力矩与飞轮期望输出力矩的差异增大，影响控制效果；

d. 飞轮增益效率下降.飞轮输出力矩相对期望力矩比例减小.

综合反作用飞轮的数学模型进行分析，发现上述故障均可通过反作用飞轮的增益系数K和粘性摩擦系数v的变化来描述，例如飞轮空转可以描述为K=0，摩擦力矩增大则表示为v高于正常值等.表1给出了飞轮在各种故障模式下的K和v的变化情况.其中：vf为飞轮正常情况下的粘性摩擦系数，vb为导致飞轮停转的粘性摩擦系数，具体根据实际飞轮进行设置.

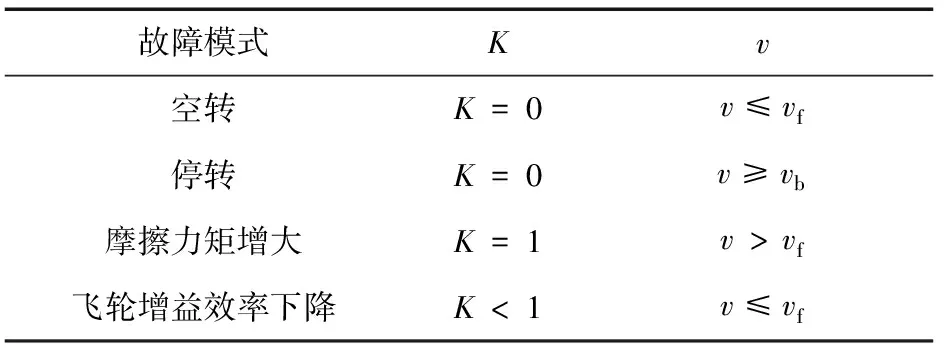
表1 飞轮故障模式及其参数化描述

表1中，v≤vf表示粘性摩擦系数处于正常情况.根据以上分析，对飞轮进行故障诊断与隔离，只需要辨识出K和v这2个参数就能知道故障的确切信息，这也是本文故障检测与分离(FDI, fault detection and isolation)的设计思想.

2 基于参数自适应投影算法的FDI

实际飞轮的时间常数td很小(如典型值td=0.001s)，故在构造观测器的时候，进一步将飞轮模型简化，得到飞轮的转速输出方程

针对上式设计如下形式的观测器：

式中：Proj为投影算子，γv>0、γK>0为权重系数，则该观测器的观测误差将满足limt→∞e(t)=0.

证明.预选 Lyapunov函数为

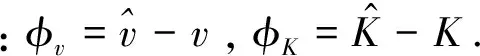
为正定函数，导数为

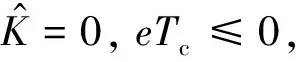
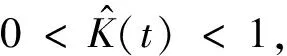
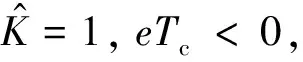
因此可得：limt→∞e(t)=0.

与传统的基于全局输入输出信息的故障诊断与隔离方法不同，该方法只利用了飞轮的局部输入输出信息[5-6].由于飞轮系统时间常数短，且一般为开环结构(力矩模式下)，故障信息往往还没有表现为整个卫星姿态系统的输出就已经反映到局部信息上，因此采用局部信息相比采用全局信息的FDI方法而言，能更早检测出故障.其次，基于全局信息的FDI方法另一个难点在于故障的隔离，特别是当多个故障同时发生时.采用局部信息的FDI可以很方便的隔离多个故障，这与全局FDI方法中通过构造多个观测器隔离故障有些类似，只是基于局部信息的FDI方法显得更为简单.

3 物理仿真验证

3.1飞轮故障软模拟

实际物理仿真实验系统的飞轮处于正常工作状态，不可能通过人为的破坏飞轮来完成故障诊断实验，因此只能采用软件的方式来模拟飞轮的故障模式.其中停转故障表现为飞轮转速在短时间急剧减小到零，此故障在飞轮正常工作时不易进行模拟，因此飞轮故障软模拟将只针对空转、摩擦力矩增大和飞轮增益效率下降3种故障.

以下用Tc表示控制器期望力矩，Tcf表示实际输入到飞轮的控制力矩，Δv=v-vf表示粘性摩擦系数相比正常值增大的部分.实验系统采用的飞轮故障软模拟方法如图1所示.

飞轮故障软模拟根据表1进行实施，对于具体的3种故障模式，可分别表示为：

1)空转模式模拟：Tcf=0·Tc；

2)摩擦力矩增大模式模拟：Tcf=Tc-Δvω；

3)飞轮增益效率下降故障模式模拟：Tcf=K·Tc.

其中，Δv=v′-vf，v′表示故障时的粘性摩擦系数.

图1 飞轮故障软模拟

3.2物理仿真结果

飞轮的转动惯量为J=0.0796kg·m2，最大输入力矩Tmax=0.06N·m，最大转速Nmax=3000r/min.其中，当飞轮转速N>2000r/min时，飞轮的输出力矩将明显下降，需要进行卸载.正常情况下，飞轮的粘性摩擦系数v=4.34×10-5N·m/(rad/s)，库仑摩擦力矩Tfc=0.00184N·m，增益系数单位化为K=1.

飞轮的初始转速偏置在450r/min左右，系统采样时间dt=50ms.给定飞轮的期望力矩信号为Tc(kdt)=0.05sin(0.2πkdt)，其中k=0,1,2,….

以下为针对飞轮正常、空转、摩擦力矩增大、增益效率下降4种情形的物理仿真实验结果.

a.正常情况下的物理仿真

对飞轮正常情况的仿真主要用于验证飞轮模型参数的正确性和观测器在当前测量环境下的有效性.图2(a)所示为飞轮转速输出实测曲线，由于飞轮转速测量存在误差，导致通过差分计算的飞轮输出力矩存在较大的干扰(如图2(b)所示的毛刺).

设计数字滤波器对飞轮的转速测量信号进行滤波，系统采用三阶巴特沃斯滤波器对飞轮测得的转速进行滤波，滤波器的形式如下：

其中，滤波器的截至频率为56.5488Hz.

图3所示为经过滤波后的力矩输出曲线与期望力矩曲线之间的比较.经比较可知，飞轮处于正转时，由于摩擦力矩的作用，飞轮的输出力矩比实际要小.

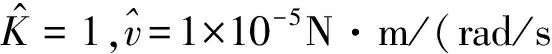
观测器对正常情况下的K和v的辨识误差分别为-0.22%和-0.85%.

图2 飞轮转速和转速差分力矩曲线

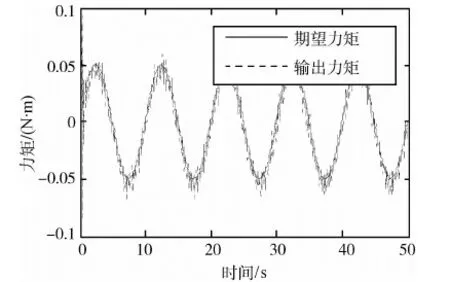
图3 滤波后的力矩曲线与期望力矩曲线

图2～4所示为飞轮正常情况下的物理仿真结果，验证了飞轮模型参数的正确性.由于飞轮转速测量噪声存在，所以还需要对所测数据进行滤波.实验中采用的是3阶数字巴特沃斯滤波器，低通滤波器的截至频率经单位化后为0.9，在保证滤波测量噪声的时候，不至于造成测量数据的失真和滞后.

同时，观测器在正常情况下对飞轮的参数的辨识，也与飞轮的标称数据相吻合，物理仿真实验验证了观测器辨识飞轮参数的有效性.

b.空转故障情形下的物理仿真

图5～6所示为空转故障情形下的物理仿真结果.空转故障发生时间为第25s，图5显示飞轮在发生空转故障后将不再响应指令输入，其转速在摩擦力矩的作用下缓慢减小.

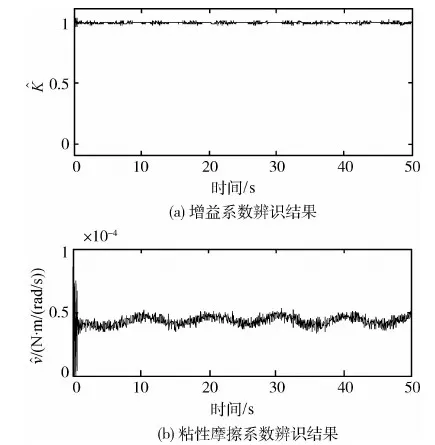
图4 正常情形下观测器的辨识结果

图5 滤波后的力矩曲线与期望力矩曲线

c.摩擦力矩增大情形下的物理仿真

图7～8所示为摩擦力矩增大故障情形下的物理仿真结果,注入的粘性摩擦系数为Δv=3.91×10-4N·m/(rad/s).故障发生时间为第25s，图7显示当飞轮摩擦力矩增大时，飞轮的实际输出力矩比期望值要小.

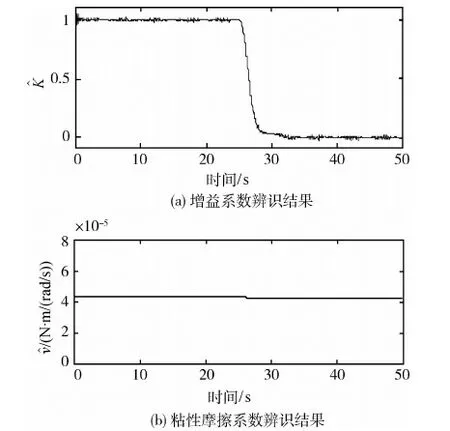
图6 空转故障情形下的观测器的辨识结果

图7 滤波后的力矩曲线与期望力矩曲线

d.飞轮增益效率下降故障情形下的物理仿真

图9～10所示为飞轮增益效率下降故障情形下的物理仿真结果，注入的飞轮增益系数为K=0.8.当飞轮增益效率下降时，飞轮的输出力矩将相比期望力矩比例减小，同时也存在摩擦力矩损失.

当采用观测器辨识出了飞轮的某个参数异常后，就可以通过查表1的方式来确定飞轮的故障模式.

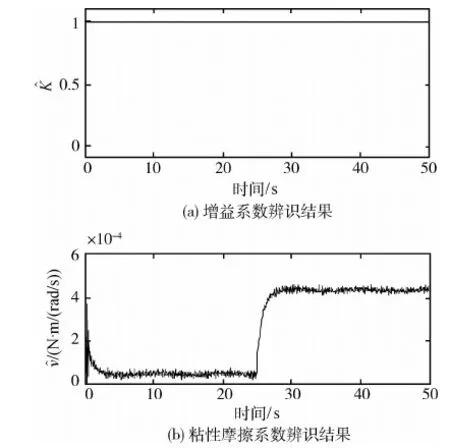
图8 摩擦力矩增大情形下观测器的辨识结果

图9 滤波后的力矩曲线与期望力矩曲线

图10 飞轮增益效率下降情形下观测器的辨识结果

4 结论

本文针对反作用飞轮的非线性数学模型，提出了一种基于参数自适应投影的飞轮故障诊断方法.该方法利用飞轮的输入输出信号，能够准确、有效地检测出飞轮空转、停转、摩擦力矩增大、飞轮增益效率下降等4种飞轮故障，并辨识出与飞轮故障相关的参数值.最后的物理仿真实验结果表明了该方法的有效性.

在三轴稳定卫星姿态控制系统中，这种只利用单个飞轮局部输入输出信息的故障诊断方法将为卫星姿控系统隔离多种故障提供方便，同时该故障诊断结果也为卫星姿控系统控制律的重构提供了良好的条件.

[1] 邢琰. 卫星闭环控制系统执行机构故障诊断及优化配置[C].第22届中国控制会议, 宜昌，2003

[2] 何英姿,张兵,吴宏鑫.递推的TLS参数估计方法及其在飞轮FDD中的应用[J].航天控制,1998,16(3):17-22

[3] 王小丽, 倪茂林. 基于自适应观测器的非线性系统故障诊断[J].空间控制技术与应用,2008,34(4):33-37

[4] Bialke B. High fidelity mathematical modeling of reaction wheel performance[C]. The 21st Annual American Astronautical Society Guidance & Control Conference, Orlando, 1998.

[5] Jovan D, Raman K. A decentralized scheme for autonomous compensation of multiple simultaneous flight-critical failures[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, California, 2002

[6] Jovan D, Joshua R, Raman K. Integrated health monitoring and adaptive reconfigurable control[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, South Carolina, 2007

ExperimentalResearchforReactionWheelFaultDiagnosisBasedonAdaptiveObserver

TIAN Kefeng1, 2, LI Minghang3

(1.BeijingInstituteofControlEngineering,Beijing100190,China; 2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190,China; 3.DepartmentofAutomation,XiamenUniversity,Xiamen361005,China)

The design of fault diagnosis for reaction wheel (RW) is presented in this paper. First, based on a nonlinear RW mathematic model, the fault modes of RW are analyzed and parameterized descriptions for faults are established. Then the observer for fault diagnosis of RW is brought forward by using an adaptive projective algorithm.The parameters are updated by the adaptive algorithm, this ensures the error of observer to be converged to zero. Finally physical simulations in normal case and three fault cases demonstrate that the proposed approach is effective and feasible.

fault diagnosis; adaptive projective algorithm; fault mode; reaction wheel; physical simulation