城镇化发展与农民收入增长关系分析①

梁春梅 肖卫东

(山东师范大学管理与经济学院,山东济南 250014;中国社会科学院研究生院,北京 100102)

城镇化发展与农民收入增长关系分析①

梁春梅 肖卫东

(山东师范大学管理与经济学院,山东济南 250014;中国社会科学院研究生院,北京 100102)

在当前条件下,加速推进城镇化进程是持续增加农民收入的根本路径选择,这是近来诸多学者潜心研究所得出的一个共同结论。本文运用协整分析、误差修正模型和 Granger因果关系三个动态计量经济模型对城镇化发展与农民收入增长的关系进行实证研究,以探讨两者之间的长期稳定关系和短期均衡关系。研究结论表明:两者之间存在长期的动态均衡关系;误差修正项对长期稳定趋势的偏离起收敛作用;从长期看,两者之间具有双向因果关系。

城镇化;农民收入增长;协整分析;误差修正模型;Granger因果关系

一、研究方法、变量与数据

单位根检验。我们首先要对所研究的相关数据进行单位根检验。若单位根过程经过一阶差分成为平稳过程,即 Yt-Yt-1=(1-B)Yt=εt,则时间序列 Yt称为一阶单整序列,记作 I(1)。一般地,如果非平稳时间序列 Yt经过 d次差分达到平稳,则称其为 d阶单整序列,记作 I(d),其中 d表示单整阶数。本文主要采用ADF检验法对相关数据进行单位根检验。ADF检验假定 Yt的数据生成过程 (DGP)为 AR(p)过程,检验方程为表1中的三个方程之一。

表1 ADF单位根的检验模型

表1的 (1)、(2)、(3)式中 ,Δ为一阶差分符号;α,β,δ,ζ为参数;εt为随机误差项 ,是服从独立同分布(iid)的白噪声过程;P为最佳滞后期数,这个滞后期数保证εt误差项的平稳性 (白噪音)。P的确定采用赤池信息 (A I C:Akaike Infor mation Criterion)准则。

协整检验。协整关系表达的是两个线性增长量的稳定的动态均衡关系。在通过单位根检验得出时间序列是平稳过程后,只有进行协整关系检验,才能判断出它们之间有协整关系,这时线性回归才具有现实意义。一般情况下,协整检验有 EG两步法与 JJ的多变量极大似然法,本文采用前一种方法。

误差修正模型。根据 Engle定理,如果一组变量之间有协整关系,则协整回归总是能被转换为误差修正模型 (ECM:Error Correction Model)。ECM反映了变量在短期波动中偏离它们长期均衡关系的程度,称为均衡误差。

格兰杰因果关系检验。协整检验结果告诉我们变量之间是否存在长期的均衡关系,但这种关系是否构成因果关系还需要进一步验证。Granger(1969)和 S ims(1972)提出的因果关系检验可解决此类问题,该检验是确定一个变量能否有助于预测另一个变量。

变量与数据。在城镇化发展与农民收入增长的协整关系研究中,农民收入增长作为内生变量,可用农村居民家庭人均纯收入来表示,即 PI。外生变量城镇化发展主要用城镇化水平来表示,而目前我国学术界在衡量我国人口城镇化水平时所采用的指标有多种。考虑到数据获得的便利性,我们主要采用市镇人口占总人口比重指标来衡量城镇化水平,虽然该指标在统计上有一定的不足和缺陷,但并不影响本文研究的精神实质。本研究采用全国的数据资料,均来自于《中国统计年鉴》(1978—2009),取样时段为 1978—2008年。其中,农民人均纯收入 PI以现价形式表示,本文使用 1978年为基期的农村居民人均纯收入指数对其进行缩减,以消除物价因素的影响。同时,为消除数据中存在的异方差,分别对两个变量取自然对数,为 LnPI,LnUR,其相应的差分序列为ΔLnPIt,ΔlnURt。

二、检验结果与实证分析

1.单位根检验

采用 EViews6.0软件,对LnPI,LnUR的单位根进行ADF检验,检验方程选取根据相应的数据图形来确定,采用A I C准则确定最佳滞后阶数,差分序列的检验类型按相应原则确定。

表2 LnPI和LnUR单位根的 ADF检验表

注:表中的Δ表示一阶差分,Δ2表示二阶差分;检验形式 (C,T,K)中的 C、T和 K分别表示单位根检验方程包括常数项、时间趋势项和滞后阶数;0是指检验方程不包括常数项或时间趋势项。

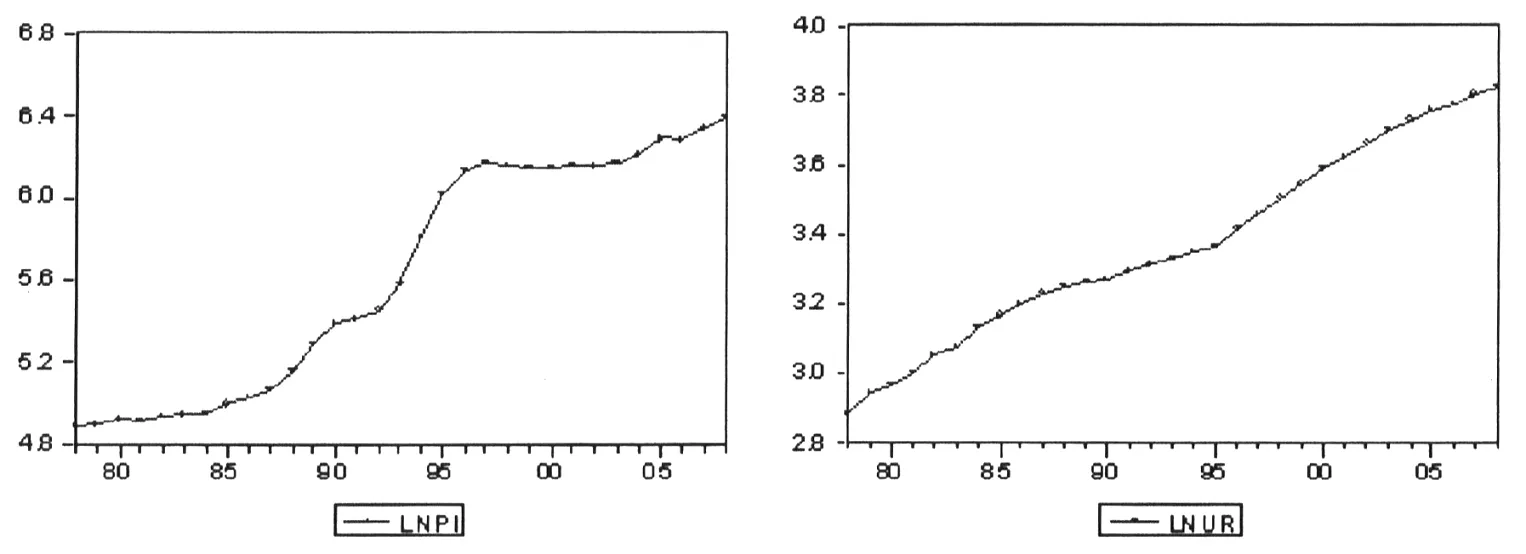
图1 中国农村居民人均纯收入和城镇化水平的变化趋势图

从图1可知,序列 LnPIt、LnURt呈上升趋势,变量数据具有明显随时间递增的特征,因此,应选取表1中包含常数项和线性时间趋势项的 (3)式作为检验方程。检验结果见表2,LnPIt、LnURt的 ADF检验统计量均大于显著性水平 0.05时的临界值,所以不能拒绝原假设,序列 LnPIt、LnURt都存在单位根,是非平稳的。

上述结果显示,未经差分的序列 LnPIt、LnURt确实存在某种时间趋势,且存在单位根,为非平稳序列。因此,应将序列 LnPIt、LnURt分别进行一阶差分,得到ΔLnPIt和ΔLnURt,再对其进行单位根检验。

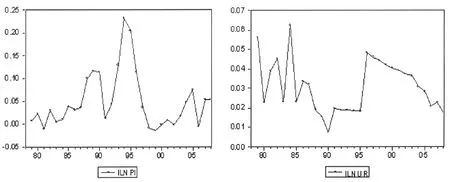
图2 中国农村居民人均纯收入和城镇化水平一阶差分的时间趋势图

从图2可知,经过一阶差分后的序列ΔLnPIt在零均值上下波动,呈无规则上升、下降趋势,宜选取表1中包含常数项和线性时间趋势项的 (3)式作为检验方程,而ΔLnURt序列具有非 0均值,但没有时间趋势,宜选取表1中包含常数项的 (2)式作为检验方程。检验结果见表2,ΔLnPIt的 ADF检验统计量大于显著性水平 0.05时的临界值,ΔLnURt的 ADF检验统计量大于显著性水平 0.05时的临界值,所以ΔLnPIt和ΔLnURt均不能拒绝原假设,序列ΔLnPIt、ΔLnURt都存在单位根,是非平稳的。检验方程及其检验效力见以下方程:

从上述 (4)、(5)式方程中的各相关参数可知,检验方程的 F检验和 t检验均很显著,检验效力较强,效果较显著。

上述结果显示,序列 LnPIt、LnURt在一阶差分后,仍然存在单位根,为不平稳序列。因此,需再将序列LnPIt、LnURt进行二阶差分,得到Δ2LnPIt和Δ2LnURt,对其继续进行单位根检验。

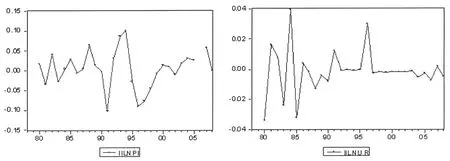
从图3可知,经过二阶差分后的序列Δ2LnPIt、Δ2LnURt在零均值上下波动,呈无规则上升、下降趋势,宜选取表1中不包含常数项和线性时间趋势项的 (1)式作为检验方程。检验结果见表2,Δ2LnPIt和Δ2LnURt的 ADF检验统计量小于显著性水平 0.05时的临界值,这表明Δ2LnPIt和Δ2LnURt均可以在 95%的置信水平下拒绝原假设,认为序列Δ2LnPIt、Δ2LnURt都不存在单位根,是平稳的。检验方程及其检验效力见以下方程:

从上述 (8)、(9)式方程中的各相关参数可知,检验方程的 F检验和 t检验均很显著,检验效力较强,效果较显著。

综上,单位根检验结果表明,非平稳序列 LnPIt、LnURt在经过二阶差分后平稳,所以,LnPIt、LnURt均为二阶单整 ,即 LnPIt～I(2),LnURt～I(2)。

2.协整检验

为了进一步分析城镇化发展与农民收入增长之间是否存在长期的均衡关系,下面对城镇化水平变量与农民人均纯收入变量进行协整分析。通过上面分析可得知,两变量序列 LnPIt、LnURt均为二阶单整,即 Ln-PIt～I(2),LnURt～I(2),满足协整检验前提,故可考虑两者之间是否存在协整关系。现用两步法对 LnPIt、LnURt变量进行协整关系检验。

第一步:估计 LnPIt对 LnURt的回归方程,协整回归模型为:

根据 1978—2008年的数据对其进行 OLS估计,得到:

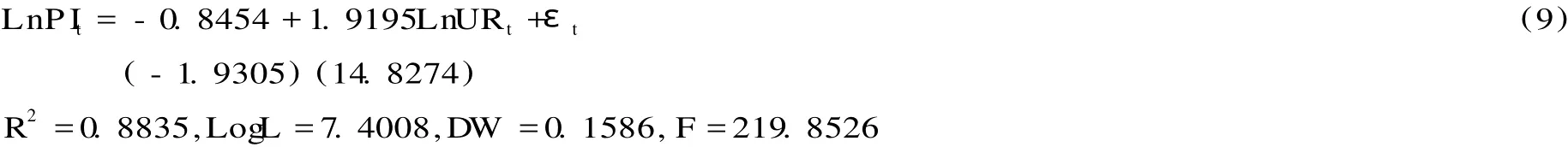
计算 OLS估计的残差,得到序列:

第二步:检验上述模型的残差项是否为平稳序列,即检验εt是否是 I(0)序列。

上述协整回归方程估计残差序列 E的取值如图4所示。对序列 e进行单位根检验,根据图4所示,ADF检验宜采用表1不包含常数项和线性时间趋势项的 (1)式检验方程。ADF检验结果见表3。从表4中可知,ADF检验统计量-2.5501都小于显著性水平0.05时的临界值,因此可认为估计残差序列E为平稳序列,^ε～I(0),这表明 LnPIt与 LnURt之间存在协整关系,(1,-2.0147)为协整向量。

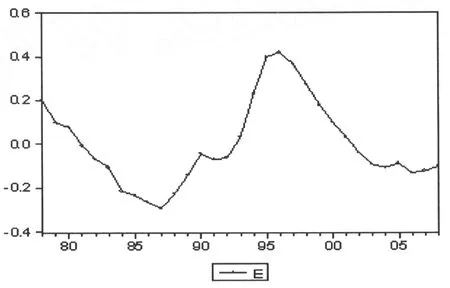
图4 残差序列 E趋势图

表3 残差序列 E单位根的 ADF检验表

根据 Engel-Granger两步法原理,上述协整回归方程不仅揭示了城镇化发展对农民收入的影响度,且表明它们之间存在长期均衡关系。从协整方程式 (9)可看出,城镇化水平每提高 1个单位,将会促进农民收入增长 1.9195个单位。因此,该协整回归方程具有现实意义。同时我们可得到协整回归方程:

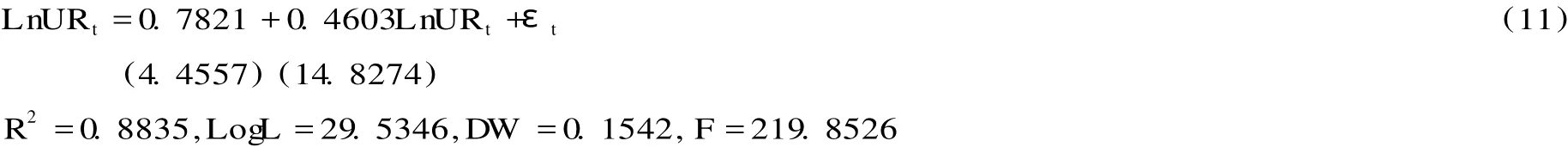
从方程 (13)式中我们可以看到,农民收入增长对城镇化发展亦有促进作用,即农民收入每增加一个单位,将会促进城镇化水平提高 0.4603个单位。因此,城镇化发展与农民收入增长之间存在着互为促进的长期关系,只是其促进作用的强度不一样,实证分析结果显示,城镇化发展对农民收入增长的促进作用强于农民收入增长对城镇化发展的促进作用。

3.误差修正模型

协整检验可用来检验两个变量之间的长期均衡关系,而其短期的变动关系要求误差修正模型的建立,用来解释变量离开均衡状态的偏差值。根据 Granger定理,一组具有协整关系的变量一定具有误差修正模型的表达式存在。本文根据“从一般到特殊”的建模方法,对 LnPIt与 LnURt之间的动态关系进行逐项检验,不显著的项逐渐被剔除,直到找到最适当的表示形式,本文建立反映 LnPIt与 LnURt之间短期动态均衡关系的误差修正模型为:

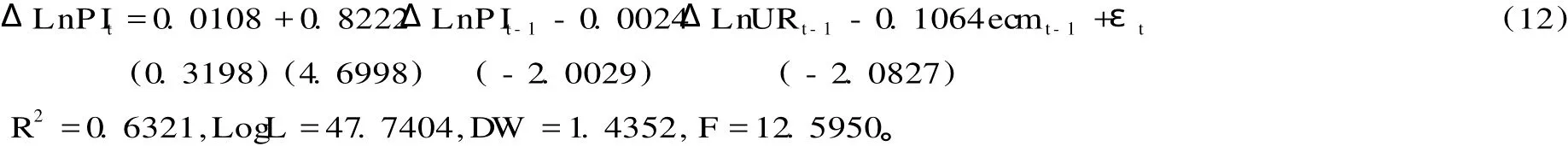
其中,ecmt-1=LnPIt+1.1501-2.0147LnURt。

误差修正模型 (14)描述了均衡误差对农民收入增长短期动态的影响,误差修正系数为负数,符合相反修正机制。从误差修正模型来看,两者的短期动态均衡关系是,城镇化水平短期内每变动 1个单位,农民收入将反方向变动 0.0024个单位,这一数值较长期协整回归方程中的要小,而且是符向的阻碍作用,这说明城镇化发展状况对农民收入增长的长期影响更为显著。同时,农民收入的短期变动,还受自身滞后一期变动的影响,其影响程度为 0.8222个单位。误差修正项 ecmt-1的系数为负 (-0.1064),说明长期均衡趋势偏离的收敛机制是:(1)当 LnPIt-1+1.1501-2.0147LnURt-1>0时,ecmt-1对农民收入增长起减少的作用;(2)当LnPIt-1+1.1501-2.0147LnURt-1<0时,ecmt-1对农民收入增长起增长的作用。ecmt-1的系数为 -0.1064,说明长期均衡趋势误差校正项对农民收入增长的调整幅度为 10.64%,具有一定程度的调节作用,同时也表明城镇化发展与农民收入增长的关系由短期偏离向长期均衡调整的速度很快,每年对上一年非均衡偏差的纠正程度为10.64%,这也从另一角度证明了城镇化发展与农民收入增长之间的长期均衡关系。

4.格兰杰因果关系检验

由于 Granger因果关系检验对滞后的阶数非常敏感,本文采用依次多滞后几阶,看结果是否具有同一性的方法。可以说,在短期内,城镇化发展并不会对农民收入增长变化产生直接的影响,而农民收入增长会影响城镇化的发展。但在一定的滞后期数上,城镇化的发展促进了农民收入的增长,同时农民收入的增长有助于城镇化的推进,两者之间具有双向因果关系。这也说明我国在采用城镇化发展促进农民收入增长的政策上,应采取长期政策而非短期政策。只有这样才能保证城镇化发展对促进农民收入增长起到持久的效果。

三、基本结论及政策含义

(1)非平稳序列 LnPIt、LnURt在经过二阶差分后平稳,均为二阶单整,即 LnPIt～I(2),LnURt～I(2)。虽然 LnPIt和 LnURt时间序列都是非平稳序列,但两者之间的线性组合却是平稳的,两者之间存在协整关系,即城镇化发展与农民收入增长之间存在长期的均衡关系。协整回归方程表明,城镇化水平每增加 1个单位,将会促进农民收入增长 1.9195个单位。

(2)从误差修正模型来看,两者的短期动态均衡关系是,城镇化水平短期内每变动 1个单位,农民收入将反方向变动 0.0024个单位,这一数值较长期协整回归方程中的要小,而且是符向的阻碍作用,这说明城镇化发展状况对农民收入增长的长期影响更为显著。误差修正系数为负数 (-0.1064),符合相反修正机制,说明长期均衡趋势误差校正项对农民收入增长的调整幅度为 10.64%,具有一定程度的调节作用,同时也表明城镇化发展与农民收入增长的关系由短期偏离向长期均衡调整的速度很快,每年对上一年非均衡偏差的纠正程度为 10.64%,这也从另一角度证明了城镇化发展与农民收入增长之间的长期均衡关系。

(3)格兰杰因果关系检验结果表明,在 1至 4期,城镇化发展与农民收入增长之间存在单向的因果关系,农民收入增长是城镇化发展的因。而在滞后 5期上,城镇化发展与农民收入增长之间存在双向因果关系。因此,在短期内,城镇化发展并不会对农民收入增长变化产生直接的影响,而农民收入增长会影响城镇化的发展。但从长期看,城镇化的发展促进了农民收入的增长,同时农民收入的增长有助于城镇化的推进,两者之间具有双向因果关系。

因此,综括上述定量的实证分析,笔者认为,城镇化发展对农民收入增长具有重大作用,我国在采用城镇化发展促进农民收入增长的政策上,应采取长期政策而非短期政策,力求避免其短期性行为,以保证其持久正向效应;在协调城镇化与农民收入增长之间的关系时,一定要遵循两者之间内在联系所决定的基本规律和基本原则,制定并实行积极的“农民收入增长先导”的城镇化发展战略。所谓以农民收入增长为先导,就是城镇化发展的第一要务是提高农民收入,以增加农民收入为主要着眼点积极推进城镇化进程,这是城镇化发展的一个根本目的。

F12

A

1003—4145[2010]08—0102—05

2010-07-15

梁春梅,女,山东师范大学管理与经济学院讲师;

肖卫东,男,山东师范大学管理与经济学院讲师、中国社会科学院研究生院博士生研究生。

(责任编辑:陆影)