对一道奥林匹克竞赛试题的再加强及猜想

●

(涡阳县第一中学 安徽涡阳 233600)

对一道奥林匹克竞赛试题的再加强及猜想

●张弓长蒲荣飞

(涡阳县第一中学 安徽涡阳 233600)

2007年女子数学奥林匹克竞赛试题中有这样一道题目：

已知a,b,c≥0，a+b+c=1，求证：

文献[1]给出了该题新的证明方法，文献[2]通过对其证明过程的思考，作了如下加强：

已知a，b，c≥0，a+b+c=1，求证:

而文献[3]给出了不能再放大的证明.笔者认为其证明过程存在2点值得商榷的地方.

(1)文献[3]中题3向题4的转化不是等价的.

由于0≤m2≤1，因此要使

恒成立，只需

即

(2)

恒成立.

式(2)是式(1)成立的充分条件，但是利用不等式恒成立求参数取值范围要用到的是充要条件，必须是等价转化才行.

(2)题4的处理值得商榷.

题4实质上是二次不等式在一个闭区间上恒成立求参数取值范围的问题.不能只用二次项系数、判别式求解,还应考虑对称轴与区间的关系.

1 试题的再加强

笔者进一步探究发现，该题还可再加强为：

已知a，b，c≥0，a+b+c=1，求证:

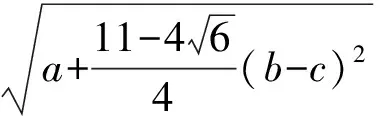
证明所证不等式等价于

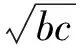
(3)

又a+b+c=1，式(3)可整理得

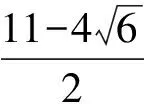
(4)

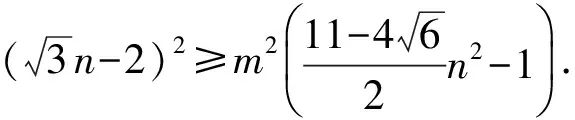
(5)

下面证明不等式(5).

-1≤m≤1,0≤m2≤1，

则

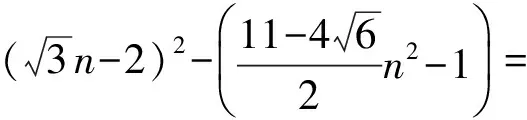
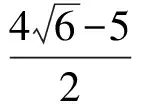
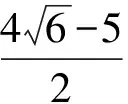
即

又0≤m2≤1，所以

2 探究之后的猜想

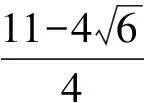
[1] 宋庆．一道女子数学奥林匹克试题的再证[J]．中学数学，2008(4)：48.

[2] 周园,李青林．对一道奥林匹克竞赛试题的“改造”[J]．中学教研(数学)，2009(1)：45-46．

[3] 李歆．对一道竞赛题系数放大问题的最后证明[J]．中学教研(数学)，2009(10)：40-41.