调和点列的妙用

●

(安康学院数学系 陕西安康 725000)

调和点列的妙用

●郭锐赵临龙

(安康学院数学系 陕西安康 725000)

1 调和点列的定义

它的一个特例,就是中学几何三角形中一个角的内角和外角平分线与对边的交点，将三角形对边的2个顶点调和分割.

引例如图1,AB为圆O的直径，C为直径延长线上一点，从点C向圆引切线CP.证明:点P在AB上的垂直射影D及点C是对于点A,B的调和共轭点.

证明由CP是⊙O的切线，得

∠1=∠PAB，∠4=∠PBA.

又AB是直径，PD⊥AB，得

△APB∽△ADP∽△PDB，

所以 ∠2=∠PAB=∠1，∠3=∠PBA=∠4，

即PA，PB分别为△CPD内角∠CPD和外角∠EPD的角平分线，于是

(AB,CD)=-1，

故点D是点C对于点A,B的调和共轭点.

2 调和点列的作图

由引例的证法，可得出求直线AB上点C的调和共轭点D的作图方法.

如图1,当点C在AB的延长线上时,

(1)过点C作以AB为直径的⊙O的切线CP切圆于点P;

(2)过点P作直径AB的垂线交AB于点D.

于是,点D便是点C对于A,B的调和共轭点.

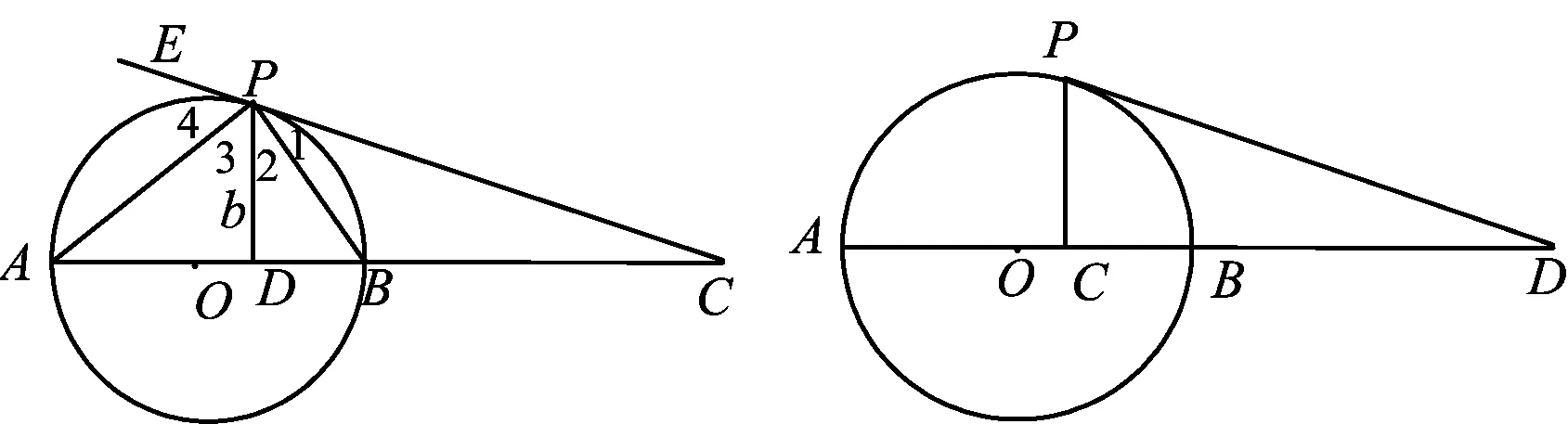
图1 图2

如图2,当点C在AB内时,

(1)过点C作AB的垂线交⊙O于点P;

(2)过点P作⊙O的切线PD交AB的延长线于点D.

于是,点D便是点C对于点A,B的调和共轭点.

3 调和点列的应用

例1[1]已知(AB,CD)=-1,证明:

证明因为

所以

AC·BD+AD·BC=0.

(1)

如图1,可得

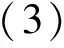
将式(2)，式(3)代入式(1),得

AC·(CD-CB)-(CA-CD)·BC=0，

化简整理得

2CA·CB=CD(CA+CB)，

即

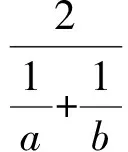
例2[2]证明平均不等式：

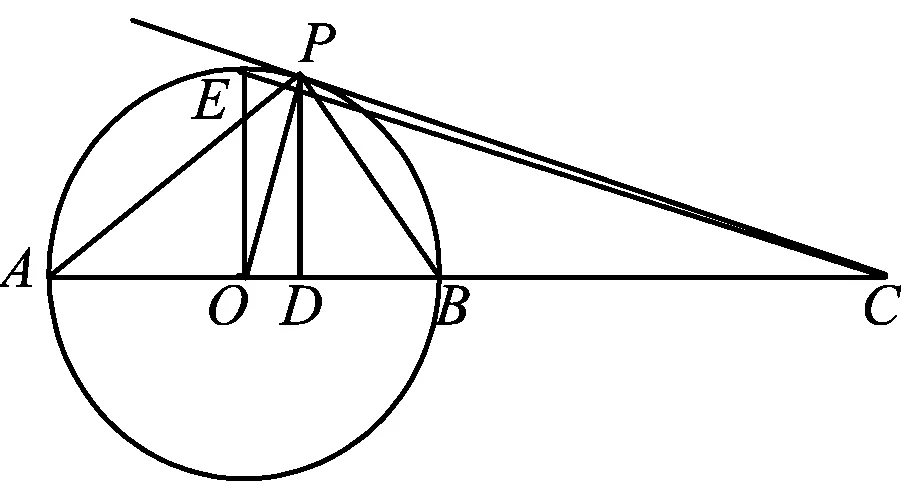
图3

证明如图3,过圆心O作OE⊥AB交⊙O于点E，连结CE.由AC=a，BC=b，得

又由CP是⊙O的切线,得

CP2=CB·CA=ab,

即

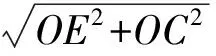
又由CE≥OC,得

(2)在Rt△OPC中，由OC≥CP,得

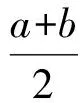
(3)在Rt△CDP中，由CP≥CD,得

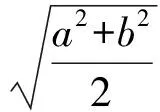
将过圆心的割线推广为不过圆心的割线时，点D还是不是点C对于点A,B的调和共轭点呢？

(2001年初中CMO竞赛试题)

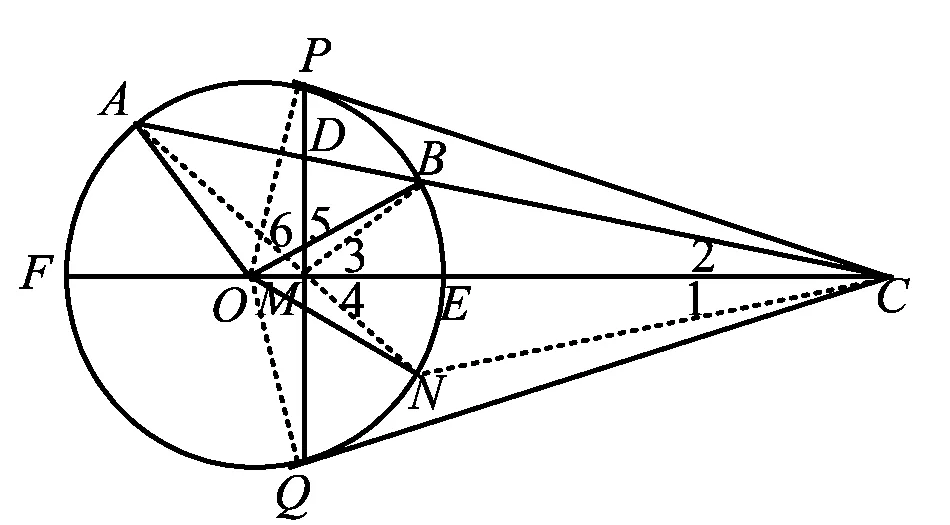
图4

证明连结AM并延长交⊙O于点N，连结BM，CN.由CP，CQ分别为⊙O的切线，连结OP，OQ,得P，O，Q，C这4点共圆.又因为P，A，Q，N这4点共圆，所以

OM·MC=PM·MQ=AM·MN.

根据交弦定理的逆定理，得A，O，N，C这4点共圆.在圆AONC中，由OB=ON，得

∠1=∠2(等弦上的圆周角相等).

因为

∠ABO+∠OBC=180°，

∠OAB+∠ONC=180°,

又OB=OA，得∠OBA=∠OAB,从而

∠OBC=∠ONC

所以

△BOC≌△NOC，

从而

CB=CN.

于是

△BMC≌△NMC，

即

∠3=∠4.

又

∠3+∠5=90°，∠4+∠6=90°，

所以

∠5=∠6.

综上所述,MD，MC分别为△AMB内角∠AMB与外角∠BMN的角平分线，即C，D调和分割点A,B,从而

(此文为安康学院大学生科技创新项目(2009AKXYDXS07)；陕西普通本科高等学校教学改革研究项目地方院校数学与应用数学专业人才培养模式创新研究(09BY70)部分成果.)

[1] 朱德祥，朱维宗.高等几何[M].2版.北京:高等教育出版社，1983:61.

[2] 赵临龙.两正数四种平均的几何统一表示及加强[J].西安文理学院学报:自然科学版,2007(3):48-50.

[3] 李文铭，罗增儒，赵临龙．初等几何教学基础[M].西安:陕西科学技术出版社，2003:164.