“平均变化率”优质课竞赛中几个精彩片断的摘录与点评

●

(射阳县教育局教研室 江苏射阳 224300)

“平均变化率”优质课竞赛中几个精彩片断的摘录与点评

●王克亮

(射阳县教育局教研室 江苏射阳 224300)

近日,江苏省盐城市举行了高中数学新课程优质课竞赛,课题统一为苏教版《普通高中课程标准实验教科书数学(选修2-2)》第1.1.1节“平均变化率”,笔者有幸作为评委聆听了11位参赛者的课.下面是参加竞赛的课中一些精彩片断的摘录与点评.

1 关于起始新课的导入

片断1师：(在播放一段山车运动视频的同时)这是世界上最高的山车,它启动时可在4 s内从0 km/h加速到190 km/h，在8 s内冲到139 m的高空，减速绕过顶端弯道，再垂直俯冲而下，第2次时速冲到190 km/h，最后20 s内在磁铁刹车的作用下穿过100 m的水平滑道，缓慢平稳地将游客带到终点…….请问:山车在运行过程中,有哪些量在发生变化?

生:位移、速度、高度.

师:对!山车在运行过程中位移的改变、速度的增减、高度的升降等这些具体可视现象中概括出来的运动过程中变量的变化情况,就是新的一章“导数及其应用”将要研究的问题.恩格斯说过:“只有微分学才能使自然科学有可能用数学来不仅仅表明状态,而且也表明过程:运动.”下面就一起来学习新的内容并深刻体会恩格斯的话的含义.

点评作为本章的起始课,该导入片断激活了苏教版教材中“导数及其应用”的章头图,将学生带入惊险刺激的运动场景,并适时地抛出恩格斯的话,让学生初步领略本章的精髓,这能充分激发学生的学习兴趣和急盼探索的欲望,体现了教材的编写意图.

2 关于问题情境的创设

片断2师：世界充满着变化,有些变化几乎不被人们所察觉,而有些变化却让人们发出感叹与惊呼.

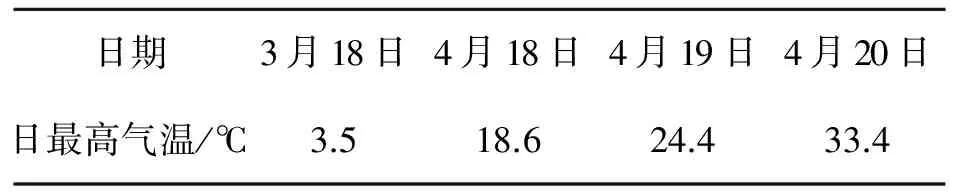
表1 气温变化表

请大家看表1,某市2009年4月20日的最高气温为33.4℃,而4月19日和4月18日的最高气温分别22.4℃和18.6℃,短短2天时间,气温陡增了14.8℃,闷热中的人们无不感叹：“天气热得太快了！”但是,如果将该市2009年3月18日的最高气温3.5℃与4月18日的最高气温18.6℃进行比较,发现两者温差为15.1℃,甚至超过了14.8℃,而人们却没有发出上述感叹,这是什么原因呢?

请同学再看一个著名的实验(用多媒体播放一个flash动画)：

第1次实验 :把青蛙放进冷水锅中,用文火慢慢加热直至沸腾,青蛙由于感受不到悄悄逼近的危险,慢慢耗尽了体力,等到灭顶之灾降临的时候,已经无力跃起了,最后不得不惨死锅中.

第2次实验:把青蛙放进煮沸的热锅里,青蛙由于骤然受热难以忍受,奋力一跃就跳出了热锅.

请大家思考:从数学角度又如何解释“水煮青蛙”的实验现象呢？

点评在苏教版教材中,“气温陡增”这个案例既是本章引言的一部分,又是第1小节的引例.日常生活中的气温变化,人人都有亲身体验,能引起学生的共鸣,是一个很好的素材.在11节竞赛课中,有10位参赛者直接运用了这个案例.

另外,《数学课程标准》对导数的教学建议是:通过大量实例的分析,经历由平均变化率过渡到瞬时变化率的过程,了解导数概念的实际背景,体会导数的思想及内涵.作为本章的第1节课,更需要通过一些实例,让学生在教师的引导下经历探索、发现、反思和一般化的过程来构建平均变化率这一概念,所以在教学中最好再补充一些有价值的例子.笔者注意到,所有的参赛教师都列举了其他的如青蛙实验、股指跳水、房价暴涨、GDP猛增、火车提速、投资收益、汽车性能等一些贴近学生生活的实例,这为后面知识的形成作好了铺垫.

3 关于知识概念的形成

片断3师：现在讨论刚才提到的气温变化问题,除了用表格外,还有什么数学工具能直观地反映上述气温的变化情况呢?

生:图像.

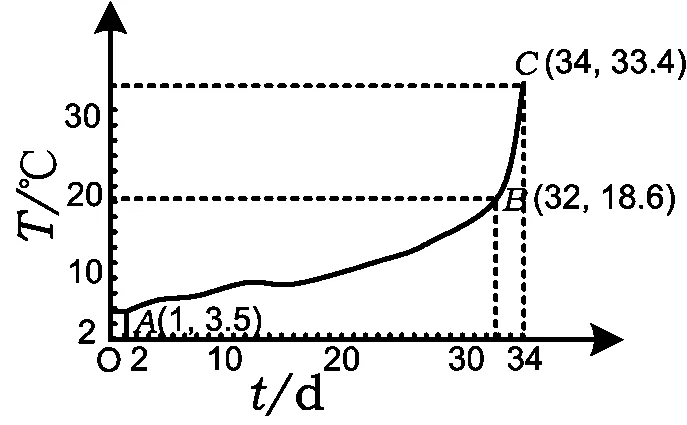
图1

师:很好!下面试着把这个图像作出来(引导学生作图,如图1所示,过程略).

从图像中可以直观地看出,曲线段AB相对平缓,而曲线段BC比较陡峭.下面需要研究的问题是:能否从数量关系上来刻画曲线的“陡峭”程度呢?请大家先自己思考,再小组讨论后发表意见.

(约3分后,学生举手发言.)

生1:看AB,BC这2段上的“天平均变化温度”.

生2:连结AB与CD,比较这2条线段的斜率.

师:这2位同学非常爱动脑筋,他们想到了2种不同的量化方法.首先按照生1的想法来量化一下看看(师生共同完成了表2).

表2 气温随时间的变化表

师:从表2中不难发现,BC段的天平均变化温度要比AB段高得多,因而对应的图像比较陡峭.下面请大家再用生2的想法算算看.

(仅几秒时间就有不少学生说两者的运算结果是一样的.)

师:我们发现这2位同学虽然思考问题的角度不同,但却有异曲同工之感.

(接着,教师引领学生提炼出平均变化率这一概念,并推广到一般函数,这些均从略.)

点评平均变化率这一概念的形成是本节课的核心所在,其处理方式可体现教者的教学思想与理念.在该片断中,教师未作任何提示,放手让学生来探究.当学生从数和形不同的角度提出了2种方案后,教师引导学生通过运算来体会这2种想法的实质的一致性,然后自然地建构出新的概念.这符合最近发展区的认知规律,一切都显得顺理成章,丝毫没有强加之意,同时也具有科学性,是一种较理想的处理方法.

4 关于书中例题的教学

片断4师:首先来看生活中的2个例子.

例1某婴儿从出生到第12月的体质量变化如图2所示,试分别计算从出生到第3月以及第6月到第12月该婴儿体质量的平均变化率.

(答案:1 kg/月；0.4 kg/月.解析过程略.)

师:请大家思考:

(1)2个不同的平均变化率所对应数值的实际意义是什么?

(2)该题中平均变化率值的大小与变量变化的快慢之间的关系如何?

(3)平均变化率的大小与曲线陡峭程度的关系如何?

图2 图3

(师生研讨过程略.)

师:(教师课前准备了实验器材,课上按照图3所示做实验)下面做一个演示实验,请同学们观察容器甲中水的体积变化的快慢情况.演示2次后,请问容器甲中的水的体积是如何变化的?

众生:减少得越来越慢.

师:对!下面请看例2.

例2水经过虹吸管从容器甲中流向容器乙,经过ts后,容器甲中水的体积V(t)=5×e-0.1t(单位:cm3),请计算:

(1)第1个10 s内V的平均变化率；

(2)第2个10 s内V的平均变化率.

(答案:(1)-0.316 1 cm3/s；(2)-0.116 2 cm3/s.解析过程略.)

师:请大家思考:

(1)2个答案中的负号有什么实际意义?

(2)2个10 s内,平均变化率的大小与容器甲中水的体积变化的快慢有着怎样的关系?

(3)一般地,平均变化率的值与变量变化快慢的关系如何?

(师生研讨过程略.)

师:下面再请大家看2个例子.

例3已知函数f(x)=2x+1,g(x)=-2x,分别计算在区间[-3，-1]，[0，5]上f(x)及g(x)的平均变化率.

(答案:f(x)对应的答案均为2；g(x)对应的答案均为-2.解析过程略.)

师:请大家思考:

(1)你能发现一次函数y=kx+b在区间[m,n]上的平均变化率有什么特点吗?

(2)你能解释其中的道理吗?

(师生研讨过程略.)

师:一次函数是这样的,那么,二次函数又如何呢?请大家看例4.

例4已知函数f(x)=x2,分别计算函数f(x)在区间[1,3],[1,2],[1,1.1],[1,1.001]上的平均变化率.

(答案:4；3；2.1；2.001.解析过程略.)

师:再请大家思考:

(1)上述几个答案有什么规律,其变化趋势如何?

(2)若将区间改成[0.9,1],[0.99,1],[0.999,1],答案如何?

(3)若将区间改成[1,1+t]和[1-t,1](其中t>0),答案又如何?

(4)你想到了什么?

(师生研讨过程略.)

点评在该片断中,教师在每道例题的后面都用几个问题来引领学生进一步领悟有关知识和作必要的拓展,开发了例题的潜在价值.如此设计,通过例1与例2的教学,至少使学生明白了:(1)平均变化率有着广泛的实际背景,如例1源于实际生活,而例2则基于一种物理现象；(2)平均变化率可正、可负、也可以为0；(3)平均变化率的绝对值越大,变量变化得越快,对应的曲线也就越陡峭.通过例3的讨论,学生不仅清楚了一次函数y=kx+b在区间[m,n]上的平均变化率的规律,而且还能从数与形2个角度解释其道理.学了例4之后,学生能直观地看到,当区间的右端点或左端点向区间的定端点1逼近时,所得到的平均变化率会逐步趋近数字“2”.若再借助几何画板来演示割线的变化趋势,则学生可进一步感悟到:用平均变化率来量化一段曲线的陡峭程度尽管是“粗糙不精确的”,但是随着区间的无限变小,这种量化便“从粗糙逼近精确”.

这里对例2的处理可谓别具一格,不仅用一个演示实验来引入,让学生先有一个直观的体验,而且比教材中原例题加算了第2个10秒内体积的变化情况,使问题有了可比性,从而增加了例题的作用.

在教材中,例4排在例3的前面,而该片断中先讲一次函数后讲二次函数,这样由浅入深,显得自然；更重要的是,上述二次函数之后的拓展,恰好为后面新课的引入留下了铺垫.

5 关于课堂结尾的设计

片断5师:刚才,我们学习了平均变化率这一概念,并解决了一些与之相关的问题,下面请大家列举一些与平均变化率有关的例子.

生1:身高在不同年龄段的生长情况；

生2:化学反应在不同时段的变化情况；

生3:房价在不同时期的涨跌情况；

生4:强台风的移动速度的变化情况.

(见学生不再发言,教师自己作了补充.)

师:请大家看图4,这是德国著名的心理学家艾宾浩斯提出的遗忘曲线,这张图说明遗忘有着什么样的变化规律呢?

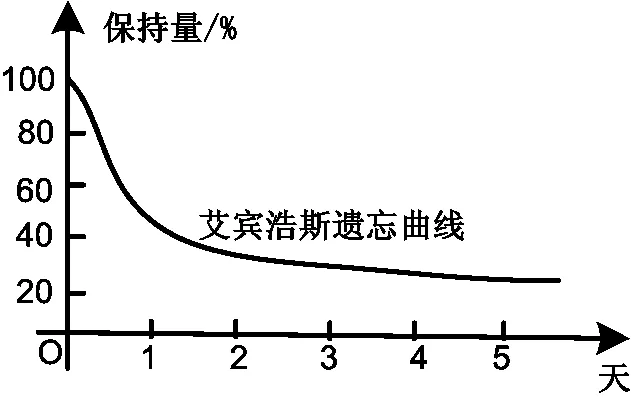
图4

生5:学习后,刚开始知识遗忘得快,然后遗忘的速度会变得越来越慢.

师:正是如此.希望大家能从该图中获得一些启示,并用来指导自己的学习.

点评在新课标中,对导数的呈现方式由以前的“极限”理论为基础变成了以“体验”为主的做法,让学生多列举身边的例子是教学参考所给的教学建议.该片断将这一活动安排在课的末尾,使得学生有话可说,效果不错.而教师补充的遗忘曲线这个例子,既符合本节课所讲的要点,又能向学生介绍有用的知识,让学生从中得到启发,真可谓是画龙点睛.

[1] 中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2003.