应用直线参数方程解比例竞赛题
2010-12-01
●
(泰州实验学校 江苏泰州 225300)
应用直线参数方程解比例竞赛题
●于志洪
(泰州实验学校 江苏泰州 225300)
众所周知,由定比分点公式
可求出分点M的坐标(x,y).在此,若以变数λ为参数,l为过点M1(x1,y1),M2(x2,y2)的直线,则对于每一个不等于-1的参数λ,l上都有1个点与之对应;反之,对于l上的除点M2外的每一个点M都有一个值λ与之对应,即有下面的一一对应关系:
{λ:λ∈R,λ≠-1}↔{M:M∈l,M≠M2},
因此,方程
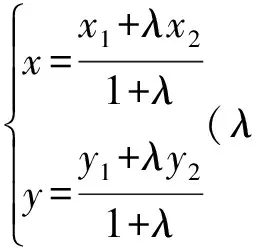
(1)
是直线l的参数方程.

下面用直线参数方程来解竞赛题.
1 求比值
例1在△ABC中,已知D为BC的中点,E为AD的中点.又BE的延长线交AC于点F,求AF∶FC.
(2007年河南省焦作市初中数学竞赛试题)
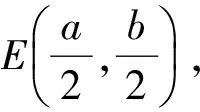
又直线AC的两点式参数方程为
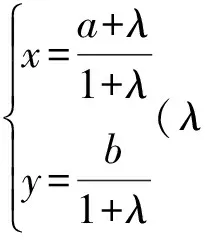
(3)
将式(3)代入式(2),得
(a+λ)b-(a+2)b+b(1+λ)=0,
解得

即
AF∶FC=1∶2.

图1 图2
2 求连比值
例2在△ABC中,D,E是BC的三等分点,M是AC的中点,BM分别交AD,AE于点G,H,则BG∶GH∶HM=
( )
A.3∶2∶1 B.4∶2∶1
C.5∶4∶3 D.5∶3∶2
(2008年江西省南昌市高中数学竞赛试题)
解建立如图2所示的直角坐标系.设A(2a,2b),C(6,0),则D(2,0),E(4,0),M(a+3,b).由两点式得AD的方程为
bx+(1-a)y-2b=0,
(4)
AE的方程为
bx+(2-a)y-4b=0.
(5)
又BM的两点式直线参数方程为
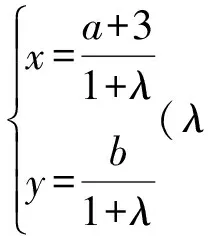
(6)
将式(6)代入式(4),得
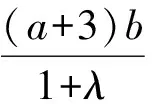
解得
λ=1,
即

(7)
又将式(6)代入式(5),得
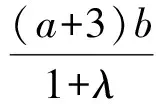
解得
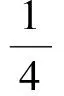
即

(8)
设BG=m,GH=n,HM=p,则由式(7),式(8)得
即
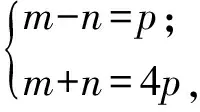
解得

因此
BG∶GH∶HM=m∶n∶p=

5∶3∶2.
故选D.
3 证四线段成比例
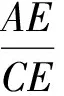
(2007年湖南省沅江市初中数学竞赛试题)
证明建立如图3所示的直角坐标系,则EDF的方程为
设A(a,b),C(c,d),则B(-c,-d),从而直线AC的两点式参数方程为
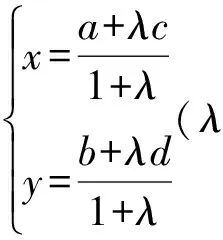
(10)

(11)
把式(10)代入式(9),可得
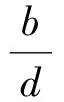
即
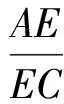
从而
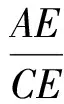
把式(11)代入式(9)可得
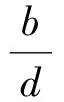
即

因此
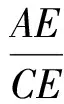
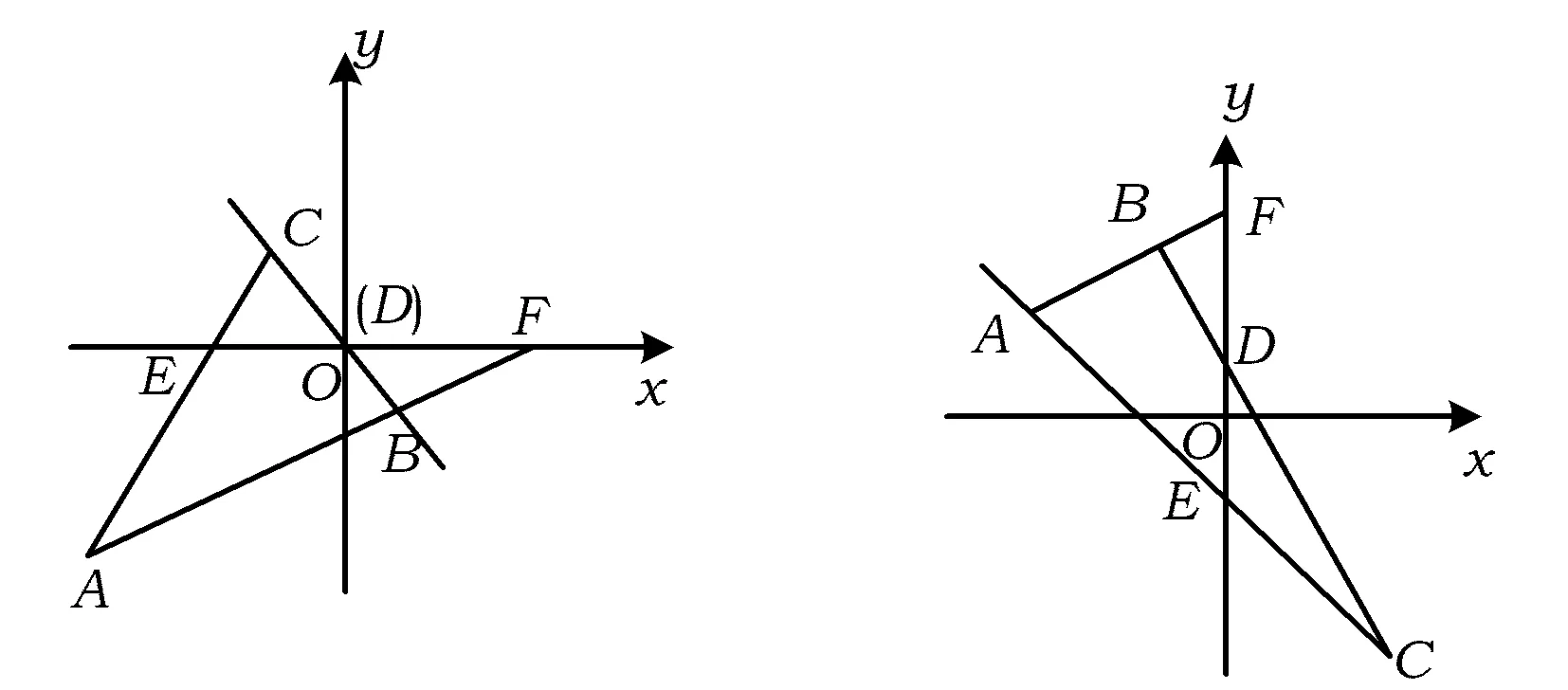
图3 图4
4 证线段比积的关系
例4(Menelaus定理)一直线截△ABC的边BC,CA,AB或其延长线于点D,E,F,求证:
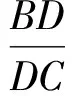
(2007年浙江省舟山市初中数学竞赛试题)
证明建立如图4所示的直角坐标系,则EDF的方程为
x=0.
(12)
设A(x1,y1),B(x2,y2),C(x3,y3),则直线CA的两点式参数方程为
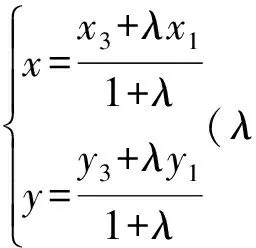
(13)
把式(13)代入式(12)可得

同理可得
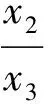
因此
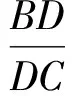
5 证线段比和的关系
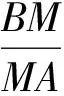
(2008年贵州省毕节市高中数学竞赛试题)
证明建立如图5所示的直角坐标系,则l的方程为
y=0.
(14)
设A(x1,y1),B(x2,y2),C(x3,y3),则
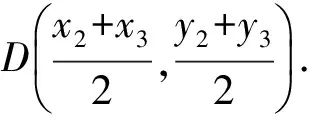
又直线AB的两点式参数方程为

(15)
把式(15)代入式(14),得
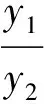
从而

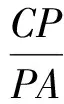
从而


综上所述,应用直线的两点式参数方程解、证这类问题时,首先要建立直角坐标系,设置好有关各点的坐标,写出一条直线的普通方程,再列出与这条直线相交的另一条直线的两点式参数方程,然后将参数方程代入普通方程中求出λ的值,按照结论要求解、证即可.

图5 图6
一般说来,这类问题有如下推广.
定理1已知D和E分别是△ABC的边BC和CA(或其延长线)上的点,AD与BE交于点F.
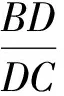
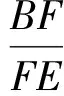

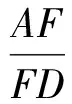
证明建立如图6所示的直角坐标系.设C(1,0),A(a,b),则由定比分点坐标公式得
由两点式得AD的方程为
b(1+m)x+(m-a-am)y-mb=0.
(16)
又直线BE的两点式参数方程为
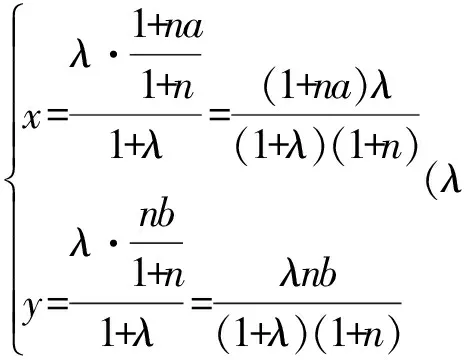
(17)
把式(17)代入式(16),得
λb(1+m)(1+na)+ (m-a-am)λnb-
mb(1+λ)(1+n)=0,
整理得
λ-m-mn=0,
从而
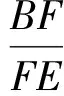
结论(1)得证.
结论(2)的证明与结论(1)类似,证明留给读者完成.
通过上述研究可知,直线两点式参数方程在竞赛中的应用不可忽视,上述比例问题的推广也通俗易懂.此专题内容不仅符合新课程改革关于“拓宽视野,加强研究”的理念要求,而且利于学生接受,适合教师讲解.实践表明,研究课本中定理、公式的应用及推广,对于帮助学生融会贯通“双基”知识,培养学生的创新意识和探索精神,对于帮助学生提高综合解题水平、理解课本内容、启迪思维、开拓视野,均很有益处.
为此,笔者认为,作为一名中学数学教师,在今后的教学过程中,有目的地引导学生对一些结合课本内容的专题进行研究,是很有必要的.
[1] 于志洪.应用直线两点式参数方程解几何题[J].海南教育学院学报:综合版.1997,8(2):11-12.
