一个不等式的再思考
2010-12-01临龙
中学教研(数学) 2010年1期
● 临龙
(安康学院数学系 陕西安康 72500)
一个不等式的再思考
●赵克赵临龙
(安康学院数学系 陕西安康 72500)
在文献[1]中,笔者提出了一个不等式,并给出了证明过程.
定理1已知a,b,x,y∈R+,μ,λ∈R+,且μ>λ,则

本文旨在变换或扩大不等式(1)的已知条件,得出了一些优美的结论.
命题1若a,b,x,y,∈R+,μ>λ>0,且x+y=1,则

分析不等式(2)的证明可参照不等式(1)的证明过程,在此不作详细说明.
在不等式(1)中,若x,y为三角函数的正弦和余弦时,则它们的指数或偶或奇.若λ为偶数,则有不等式(2);若λ为奇数,其结果又该如何?
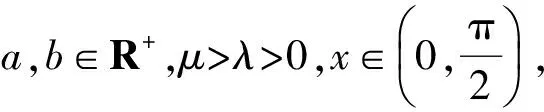

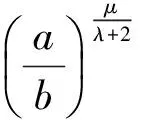
证明原不等式可化为
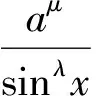
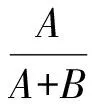



命题2若a,b,x,y∈R+,λ<μ<-1,则
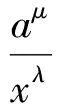
证明因λ<-1,μ<-1,令μ=-p,λ=-q,则p>1,q>1,因此
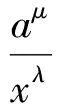
成立.
推论2若a,b∈R+,0

结合以上的相关叙述,同样给出如下结论.
命题3若a,b,x,y∈R+,-1<λ<μ<0,则

命题4若a,b,x,y∈R+,μ>λ>0,则

本文限于篇幅长度,对命题3和命题4不再作过多的说明.同时,本文在文献[1]的基础上,改变不同的条件,对问题进行了更深入的探究.以上命题1-4以及推论1、推论2都满足不等式在一定条件下推广为更一般化的形式.有兴趣的读者请自行证明.
(本文为安康学院大学生科技创新项目(2008AKXYDXS04);安康学院重点扶持学科《基础数学》建设项目(AZXZ0107)部分成果.)
[1] 赵克,赵临龙.一个不等式的再讨论[J].中学数学教学参考,2009(9):15-17.
[2] 罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,1997.
[3] 匡继昌.常用不等式[M].济南:山东科学技术出版社,2004.
