一道中考题的追溯、提炼及其应用
2010-12-01
●
(定远中学 安徽定远 233200)
一道中考题的追溯、提炼及其应用
●韩敬
(定远中学 安徽定远 233200)
作为衡量学生学习成果的中考试题,凝聚着中考命题专家们的智慧,体现了新课改精神和命题的导向.深入研究中考试题的命题背景以及与往年中考试题的关系,并从中总结规律,对于提高学生的解题能力是一个很好的途径.下面以2009年安徽省数学中考试卷中的一道题为例说明,以飨读者.
1 试题及其解析
例1如图1,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于点F,ME交BC于点G.
(1)写出图中3对相似三角形,并证明其中的1对;
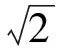
(2009年安徽省数学中考试题)
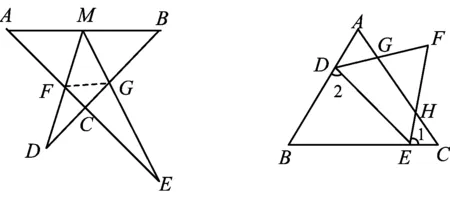
图1 图2
分析(1)△AMF∽△BGM,△DMG∽△DBM,△EMF∽△EAM.以下证明△AMF∽△BGM.由∠AMG=∠MGB+∠B且∠AMG=∠AMF+∠DME,可得
∠AMF=∠MGB.
又因为∠A=∠B,所以
△AMF∽△BGM.
(2)略.
2 追溯
由这道题联想到课本中的一道习题:沪科版第95页C组复习题的第1题.
例2如图2,△ABC,△DEF均为正三角形,点D,E分别在边AB,BC上,请在图中找出一个与△DBE相似的三角形并证明.
分析由题意知:∠B=∠C=∠DEF=60°,不妨找△ECH与△DBE相似.因为∠1+∠DEF=∠2+∠B,所以∠1=∠2.又∠B=∠C,故
△ECH∽△DBE.
同理可得 △DAG∽△DBE;△GFH∽△DBE.
因此与△DBE相似的三角形有△DAG,△GFH,△ECH.
3 对比反思、提炼基本图形
由例2中的隐含条件“∠B=∠C=∠DEF=60°”到例1中的“∠DME=∠A=∠B=α”这一变化,可以看出例1的形成是以例2为背景的,例1是例2的延伸、拓展.这里体现了“一般与特殊”的关系,这样的关系促使我们再来思考例1.经过探索发现:如图3所示,在△ABC中,AB=AC,当∠B=∠C=∠EPF=α时,总有△BPE∽△CFP;
类似地,把这里的“等腰三角形”替换为“等腰梯形”,如图4所示.显然当∠B=∠C=∠EPF=α时,也总有△BPE∽△CFP.特别地,当∠B=∠C=∠EPF=90°时,如图5所示,显然有△BPE∽△CFP,于是得到了3个较为常见的基本图形.
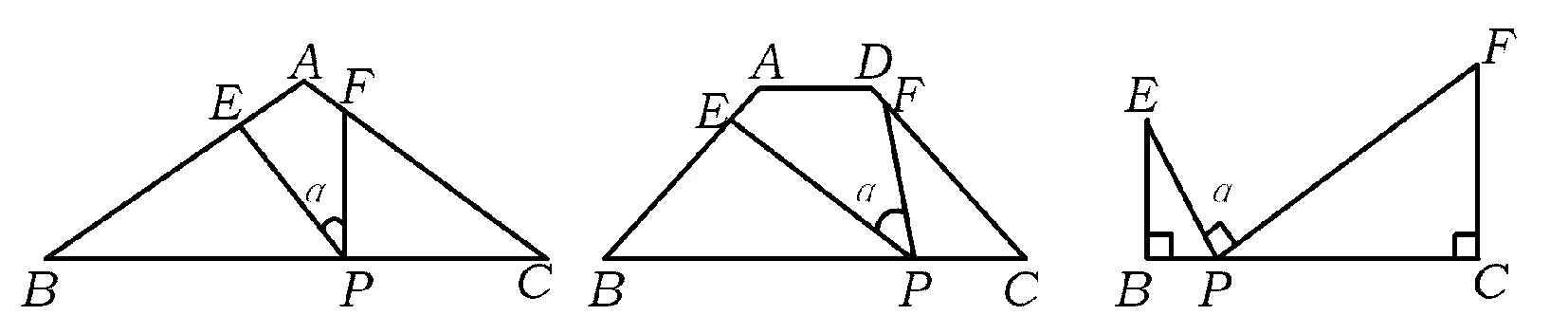
图3 图4 图5
4 探索应用
从近几年的中考数学试题可以发现这3个基本图形频频出现,命题者以此模型为背景,直接或间接地利用这样的模型,命制出一批构思巧妙、立意新颖的好题.
4.1 直接应用
例3如图6,在梯形ABCD中,AD∥BC,AB=DC=AD=6,∠ABC=60°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=120°.设AE=x,DF=y.
(1)求y与x的函数表达式;
(2)当x为何值时,y有最大值,最大值是多少?
(2007年江苏省南京市数学中考试题)
分析(1)由∠ABC=60°,可知∠A=∠D=120°,所以∠A=∠D=∠BEF=120°.由基本图形4可得,△ABE∽△DEF,于是
AB∶DE=AE∶DF,
即
6∶(6-x)=x∶y,
整理得
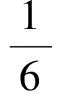
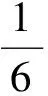
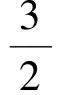
评注此题将相似三角形与二次函数的内容有机结合,解决本题的关键是解决第(1)小题.而在第(1)小题中,巧用基本图形4是迅速解决问题的突破口.由基本形易得2个三角形相似,再根据“相似三角形的对应线段成比例”这一性质,从而得到了函数表达式.要完成第(2)小题,只要对这个表达式进行正确的配方即可.
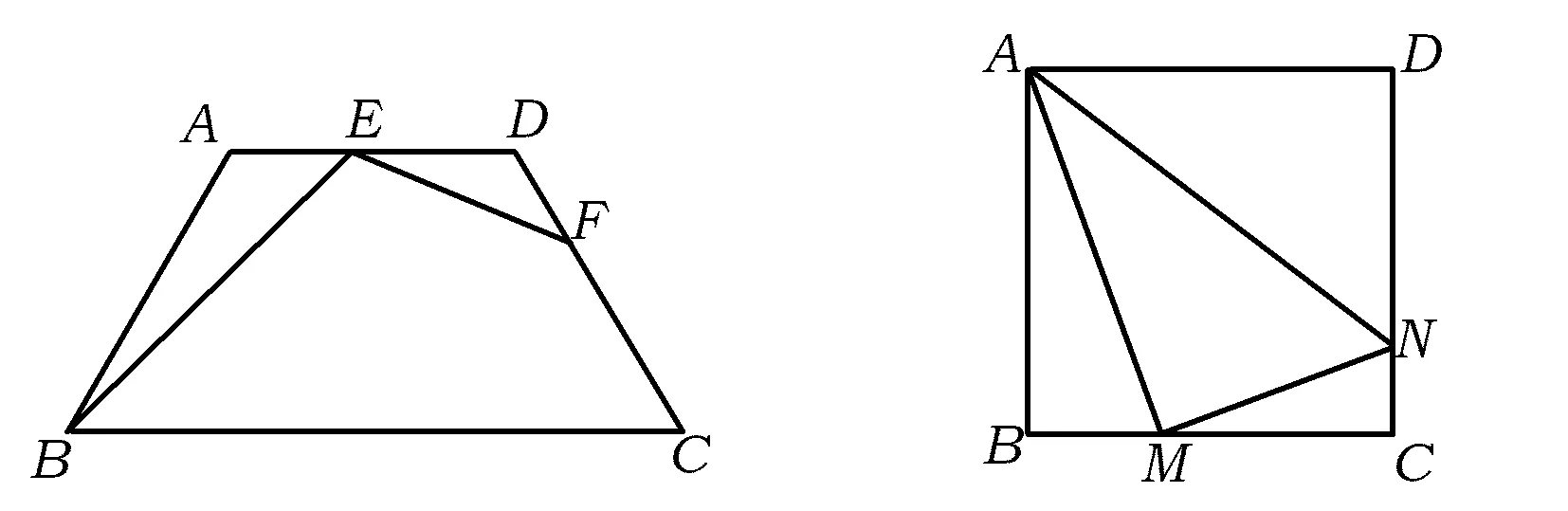
图6 图7
例4如图7,正方形ABCD边长为4,M,N分别是BC,CD上的2个动点,当点M在线段BC上运动时,保持AM和MN垂直.
(1)证明:Rt△ABM∽Rt△MCN.
(2)设BM=x,梯形ABCN的面积为y,求y与x之间的函数关系式.当点M运动到什么位置时,四边形ABCN的面积最大,并求出最大面积.
(3)当点M运动到什么位置时,Rt△ABM∽Rt△AMN,求此时x的值.
(2009年广东省数学中考试题)
分析(1)由∠B=∠C=∠AMN=90°,可得基本形图5,易得Rt△ABM∽Rt△MCN.
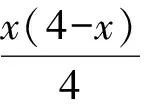
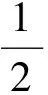

当x=2时,y取到最大值,即当点M为BC的中点时,ABCN的面积最大,最大值为10.
(3)要使Rt△ABM∽Rt△AMN,只要AB∶AM=BM∶MN成立即可.由第(1)小题知Rt△ABM∽Rt△MCN,显然AB∶AM=MC∶MN,因此
BM∶MN=MC∶MN,
即BM=MC,故M为BC的中点,此时x=2.
评析这是一道关于点运动型的综合性较强的试题.本题把相似三角形的内容与二次函数内容巧妙地融合,对于第(1)小题,利用基本图形5,易证得2个三角形相似,这对相似三角形是解决后2个问题的必要条件;利用这对相似三角形中的成比例线段,第(2)小题顺利得解;尤其是第(3)小题,由逆向思考,再结合原相似三角形中的成比例线段,从而巧解该小题.
4.2 逆向应用
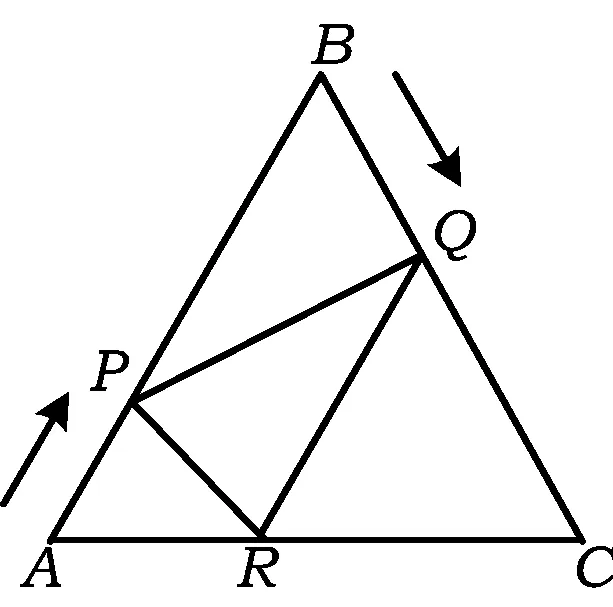
图8
例5如图8,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从点A,B出发,分别沿AB,BC匀速运动,其中点P运动的速度是1 cm/s,当点Q到达点C时,点P,Q都停止运动.设运动时间为t(s),解答下列问题:
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
(2008年福建省福州市数学中考试题)
分析(1)易证△BPQ为等边三角形.
(2)易得

(3)由QR∥BA可得,∠APR=∠QRP及BQ=AR.要使△APR∽△PRQ,只需∠A=∠QPR=60°即可.当∠QPR=60°时,有
∠A=∠B=∠QPR=60°,
可得基本图形3,易知△BQP∽△APR,所以
BQ∶BP=AP∶AR,
即
2t∶(6-t)=t∶2t,
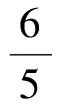
评注本题是一个关于点运动型的问题.前2个小题学生容易解答.对于第(3)小题,难度较大.若考虑到将其转化为基本图形3,巧妙地构造出2个三角形相似,利用比例线段,易求得t值.本小题运用逆向思维,把问题转化为基本图形来解决,这一转化使问题变得简单、易解,学生的逆向思维能力得到提高,也渗透了转化思想.
4.3 构造应用
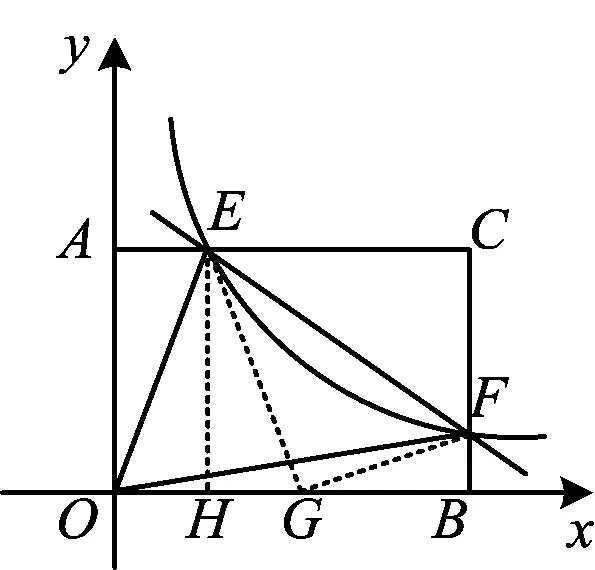
图9
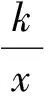
(1)求证:△AOE与△BOF的面积相等.
(2)记S=S△OEF-S△ECF,当k为何值时,S有最大值,最大值为多少?
(3)请探索:是否存在这样的点F,使得将△CEF沿EF对折后,点C恰好落在OB上?若存在,求出点F的坐标;若不存在,请说明理由.
(2008年浙江省湖州市数学中考试题)
分析(1)容易证得△AOE与△BOF的面积相等.
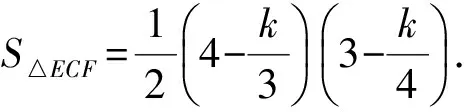
S△EOF=S矩形AOBC-S△BOF-S△AOE-S△ECF=
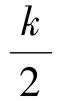
12-k-S△ECF,
因而
S=S△EOF-S△CEF=12-k-2S△ECF=
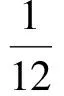
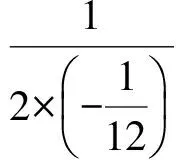
(3)假设存在点F,使得将△CEF沿EF对折后,点C恰好与边OB上的点G重合.作EH⊥OB于点H,则
∠EHG=∠GBF=∠EGF=90°.
可得基本图形5,显然△EGH∽△GFB,因此
EH∶GB=EG∶GF.
代入解得
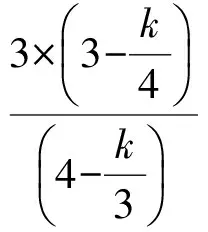
在Rt△GBF中,GF2=GB2+BF2,即
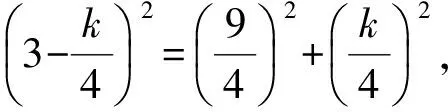
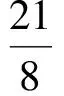
评析前2个小题考查的是反比例函数图像上点的几何意义,不难解决;第(3)小题是一个折叠型问题,又是一个关于“点是否存在型说理题”,难度较大.但在假定点F存在的情况下,巧妙地构造出基本图形5,这是解决问题的突破口,题目难度也因此大大降低.由“相似三角形对应边成比例”的性质,可求出GB,再结合勾股定理,建立方程解得k值,从而说明点F是存在的.
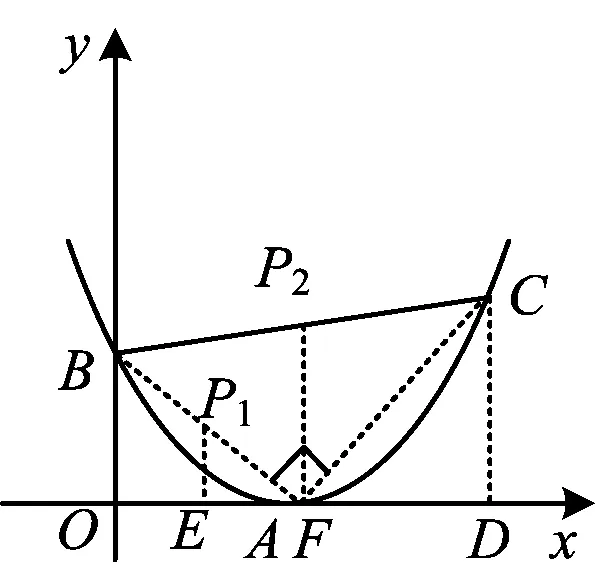
图10
例7如图10,已知抛物线y=ax2+bx+c的顶点A在x轴上,与y轴的交点为B(0,1),且b=-4ac.
(1)求抛物线的解析式.
(2)在抛物线上是否存在一点C,使得以BC为直径的圆经过抛物线的顶点A?若不存在,说明理由;若存在,求出点C的坐标,并求出此时圆心点P的坐标.
(3)根据第(2)小题的结论,你发现B,P,C这3个点的横坐标之间、纵坐标之间分别有何关系?
(2008年湖北省荆门市数学中考试题)
分析(1)易知c=1,由b2-4ac=0与b=-4ac,可得b=-1,从而
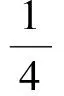
因此
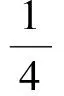
(2)假设存在满足题设条件的点C.设C(x,y),则
∠AOB=∠ADC=∠BAC=90°,
可得基本图形5,易得
△AOB∽△CDA,
于是
AO∶OB=CD∶DA,
即
2∶1=y∶(x-2),
解得
y=2x-4.
由
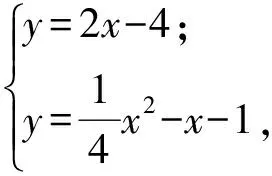
解得
x1=10,y2=16或x2=2,y2=0.
因此点C存在,且坐标为(10,16)或(2,0).
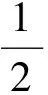
当C(10,16)时,P2为BC的中点,过点P2作P2F⊥OD于点F,可得点F为OD的中点.由梯形中位线定理,易知

所以
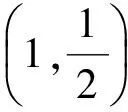
(3)设B(x1,y1),P(x2,y2),C(x3,y3),由第(2)小题的分析可知
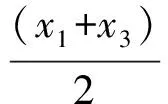
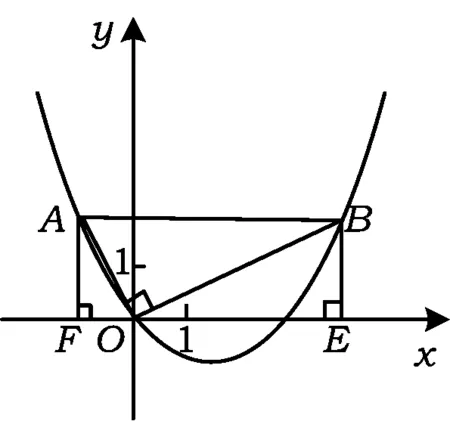
图11
评析第(1)小题利用方程思想,易得所求函数的解析式;求解第(2)小题的关键在于利用“直径所对的圆周角为直角”,巧妙地构造出基本图形5,这一转化可以说是化陌生为熟悉,大大缩短了思考时间.在假定点C存在的情况下,利用2个三角形相似及原函数的关系式,联立方程组求出点C的坐标,易判断点C存在,也由此探究出第(3)小题的结论.
例8如图11,在平面直角坐标系中,OB⊥OA,且OB=2OA,点A的坐标是(-1,2).
(1)求点B的坐标;
(2)求过点A,O,B的抛物线的表达式;
(3)连结AB,在第(2)小题中的抛物线上求出点P,使得S△ABP=S△ABO.
(2009年陕西省数学中考试题)
分析(1)过点A作AF⊥x轴,垂足为点F,过点B作BE⊥x轴,垂足为点E.由
∠AFO=∠AOB=∠OEB=90°
可得基本图形5,显然
Rt△AFO∽Rt△OEB,
所以
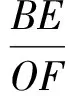
即BE=2,OE=4,故点B的坐标为B(4,2).
(2)易求得抛物线的表达式为

(3)由题意知AB∥x轴.设抛物线上符合条件的点P到AB的距离为d,则

易得d=2,显然点P的纵坐标只能是0或4.
当y=0,即

时,解得x=0或x=3,因此符合条件的点为P1(0,0),P2(3,0);
同理可得:当y=4,即

时,解得
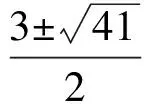
评析本题是一道融几何与代数为一体的综合性试题,此题中的3个小题的设计有梯度,后1个小题的解决都是建立在前几个小题的基础上,因此第(1)小题解答的正确与否直接关系到后2个小题.显然,巧妙地构造出基本图形5是解决本题的关键,这一构造把求点的坐标转化为相似问题来解决,体现了转化和数形结合的思想.
