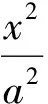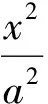圆锥曲线中三直线斜率成等差数列的3个命题

● (周庄高级中学 江苏兴化 225711) ● (戴窑高级中学 江苏兴化 225741)

圆锥曲线中三直线斜率成等差数列的3个命题

●张乃贵(周庄高级中学 江苏兴化 225711) ●邢友宝(戴窑高级中学 江苏兴化 225741)

最近笔者在研究圆锥曲线的性质时，发现了圆锥曲线中三直线斜率成等差数列的3个命题，现将之整理成文，与大家交流．希望对大家的学习和研究有所启发与帮助．

命题1过抛物线y2=2px(p>0)的对称轴上的定点M(m,0)(m≠0)的直线AB与抛物线相交于A,B两点，N是定直线l:x=-m上的任一点，则直线NA,NM,NB的斜率成等差数列．

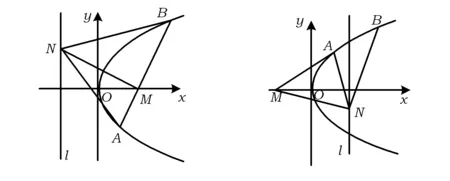
图1 图2

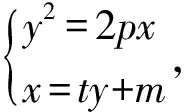
y2-2pty-2pm=0，

从而

y1y2=-pm.

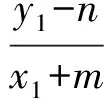
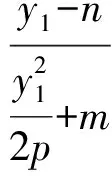
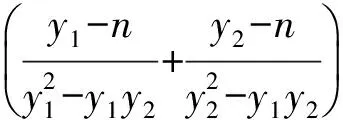
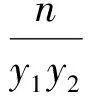
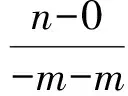
推论1M(m,0),N(-m,0)(m≠0)为抛物线y2=2px(p>0)对称轴上的2个定点，过点M的直线AB与抛物线相交于A,B两点，则∠BNM=∠ANM或∠BNM+∠ANM=180°．

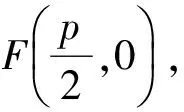
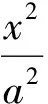
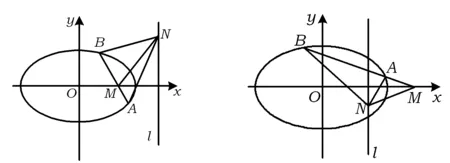
图3 图4

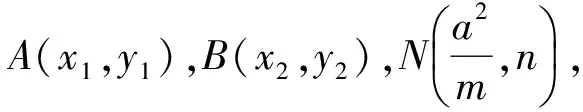
x1=ty1+m,x2=ty2+m.

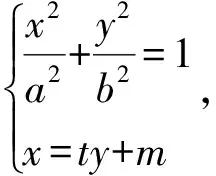
(a2+b2t2)y2+2b2mty+b2(m2-a2)=0，

从而

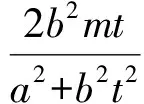
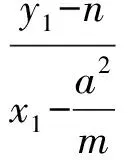
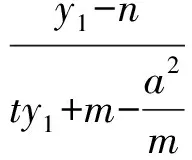
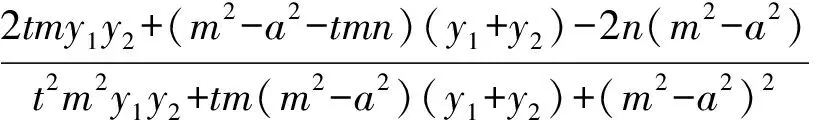
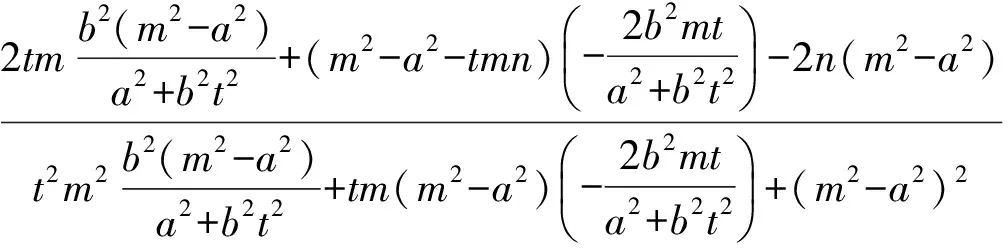
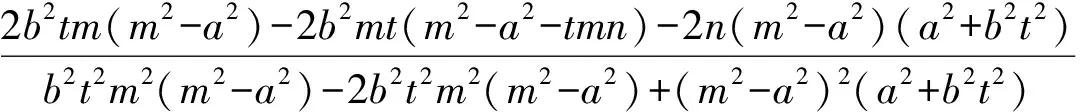
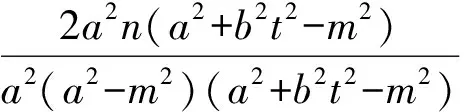
当直线AB与x轴重合时，A(-a,0)，B(a,0)，得

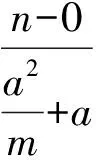
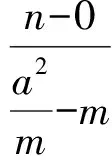
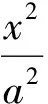
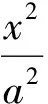
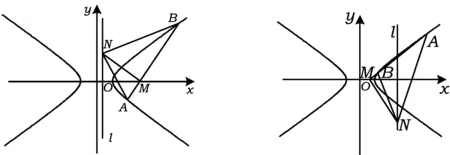
图5 图6

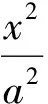
只要将命题2证明过程中的b2换成-b2，即可得命题3的证明．