以选修系列3为背景的数学高考试题赏析
2010-12-01
●
(内江师范学院数学与信息科学学院 四川内江 641112)
以选修系列3为背景的数学高考试题赏析
●赵思林
(内江师范学院数学与信息科学学院 四川内江 641112)
2003年4月,教育部颁布了《普通高中数学课程标准(实验)》(以下简称《标准》),从而使高中数学新课程改革稳步、有序地推进.高考数学命题受此影响,出现了以新课程理念为背景的命题新视角,涌现出了越来越多的体现新课程理念的好题目.《标准》中选修系列3由6个专题组成:数学史选讲、信息安全与密码、球面上的几何、对称与群、欧拉公式与闭曲面分类、三等分角与数域扩充.由此可以看出,选修系列3涉及较多的高等数学知识.这些课程过去在中学里没有出现过,这对提高学生的学习兴趣和开阔学生的数学视野是很有益的.虽然《标准》明确说明“系列3不作为高校选拔考试的内容”,但在近几年的高考试题中出现了一些涉及选修系列3内容的优秀试题,这些试题背景新颖、设计独特,有较高的思维价值和良好的检测功能.它们对引导高中数学教学、推动高中数学课程改革起到了正面的导向作用.
1 以数学史为背景
数学史是数学文化的重要组成部分,加强数学史教育是培养学生人文素养的重要举措.了解数学发展过程中的重要事件、重要人物与重要成果,对体会数学对人类文明发展的作用,提高学习数学的兴趣,感受数学家的严谨态度和锲而不舍的探索精神具有重要的意义.
例1古希腊人常用小石子在沙滩上摆成各种形状来研究数.譬如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
( )
A.289 B.1 024 C.1 225 D.1 378
(2009年湖北省数学高考理科试题)
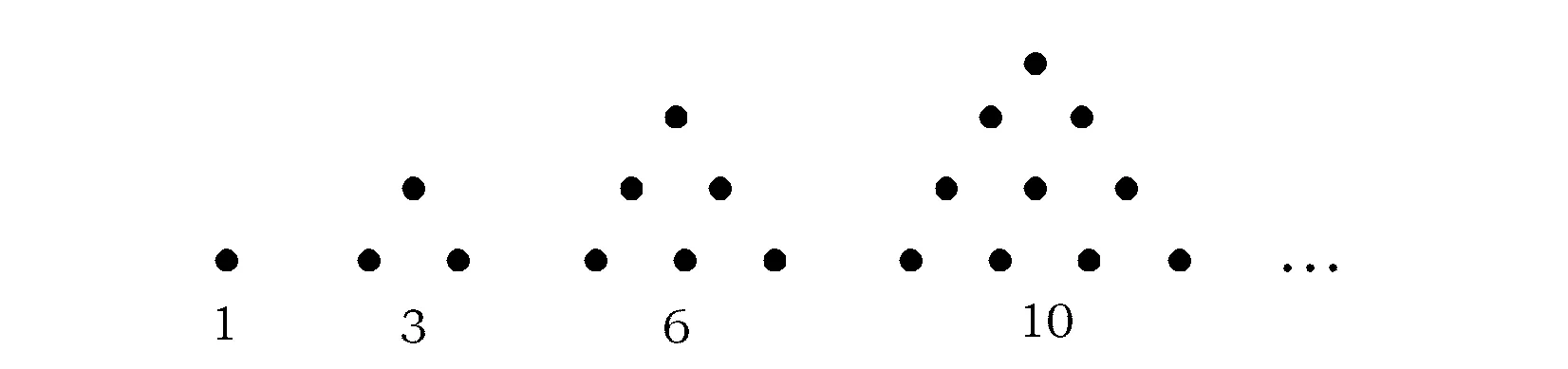
图1
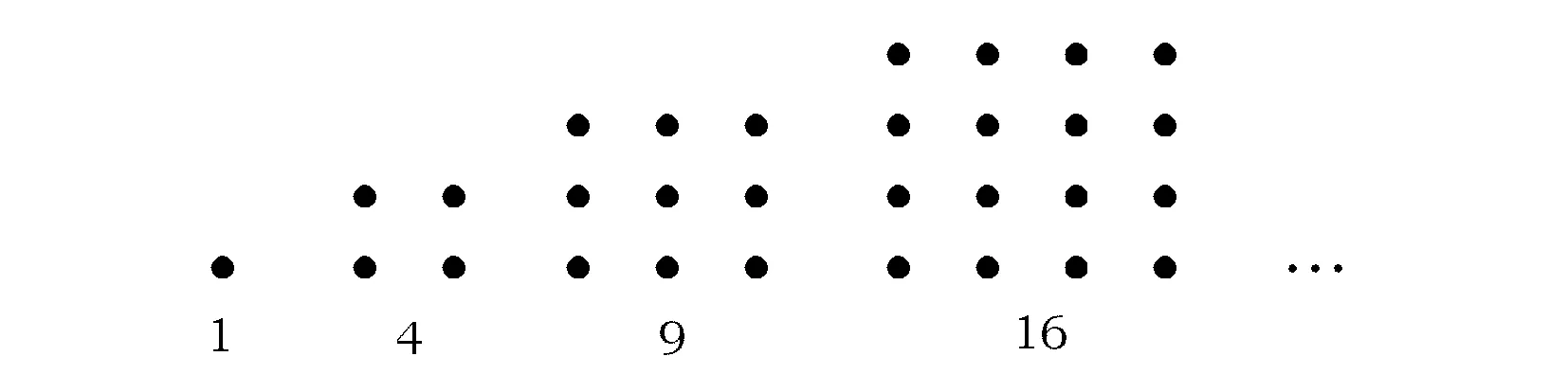
图2

例22002年在北京召开的国际数学家大会的会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由4个全等直角三角形与1个小正方形拼成的1个大正方形(如图3).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于________.
(2007年北京市数学高考文、理科试题)
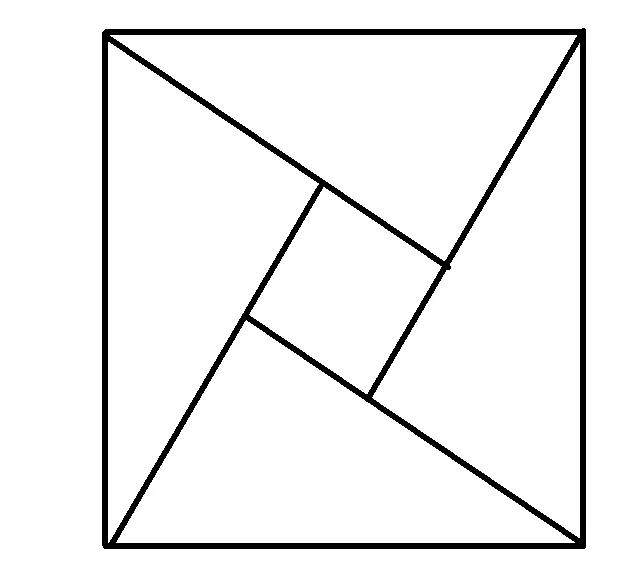
图3
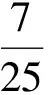
2 以信息安全与密码为背景
数论是信息安全与密码十分必要的数学基础,它在现代信息理论、信息安全、保密通信中有着非常广泛的应用.
例3为提高信息在传输中的抗干扰能力,通常在原信息中按照一定规则加入相关数据组成传输信息.设定原信息为a0a1a2,ai∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1,其中h0=a0⊕a1,h1=h0⊕a2,⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是
( )
A.11010 B.01100 C.10111 D.00011
(2008年陕西省数学高考文、理科试题)
赏析本题涉及到选修3-2中的信息安全与密码.由题意知,选择支A的原信息为101,选择支B的原信息为001,选择支C的原信息若为011,则传输信息为10110,而不应该是10111,所以C是错误的.故选C.
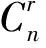
(2006年湖北省数学高考理科试题)
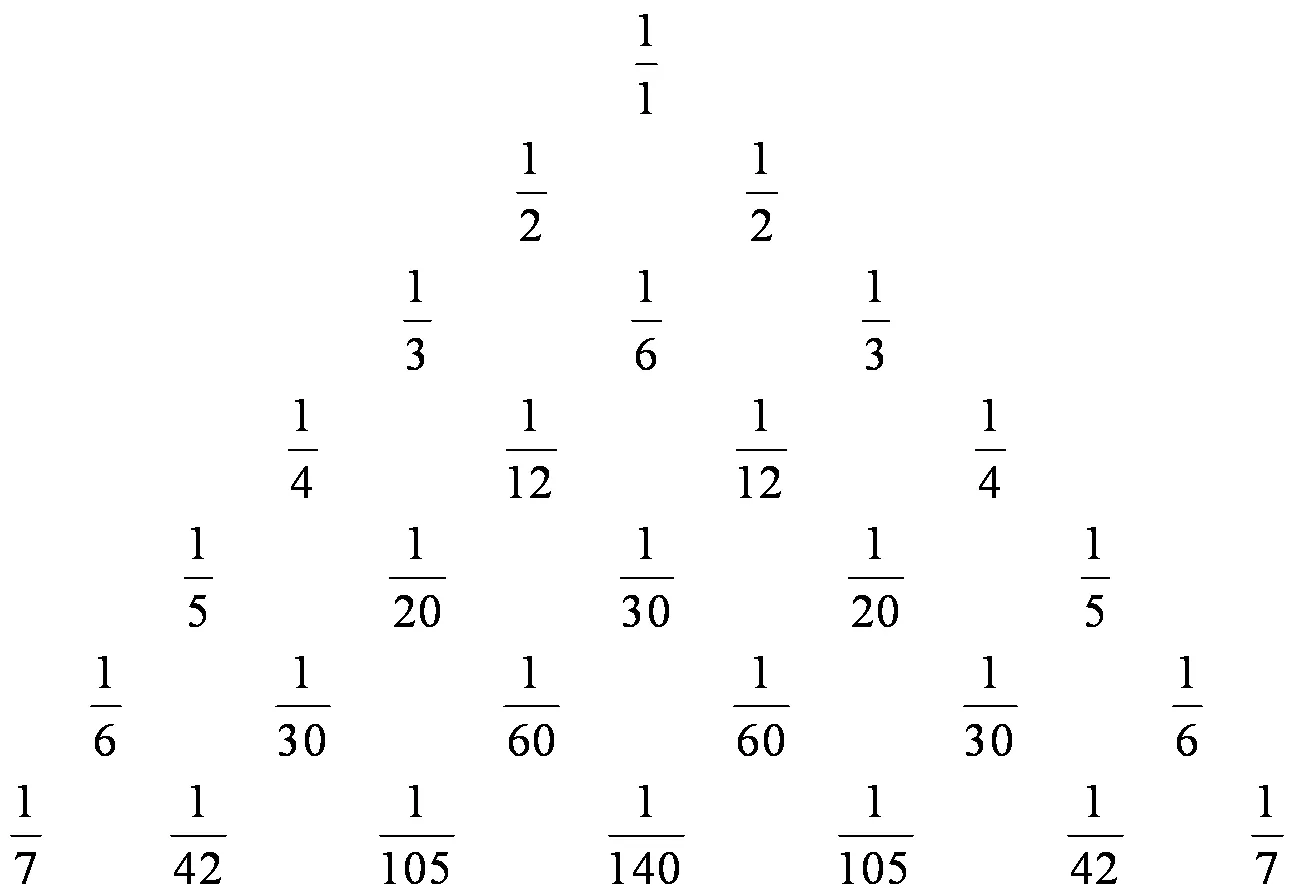
图4
赏析联想杨辉三角可以发现:在莱布尼茨三角形中,每个数都等于它脚下的2个数字之和,即
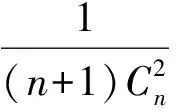
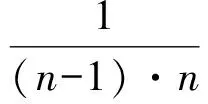
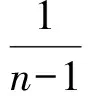
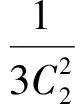
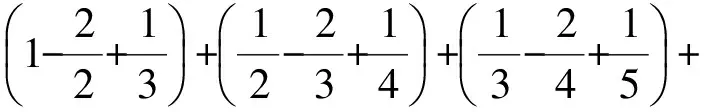

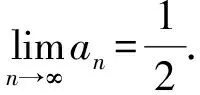
点评此题涉及到选修3-2的信息安全与密码中的初等数论,是数论中的单位分数.本题中的莱布尼茨三角形选自柯召院士、孙琦教授合著的《单位分数》第39页.
例5为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为
( )
A.4,6,1,7 B.7,6,1,4
C.6,4,1,7 D.1,6,4,7
(2007年陕西省数学高考文、理科试题)
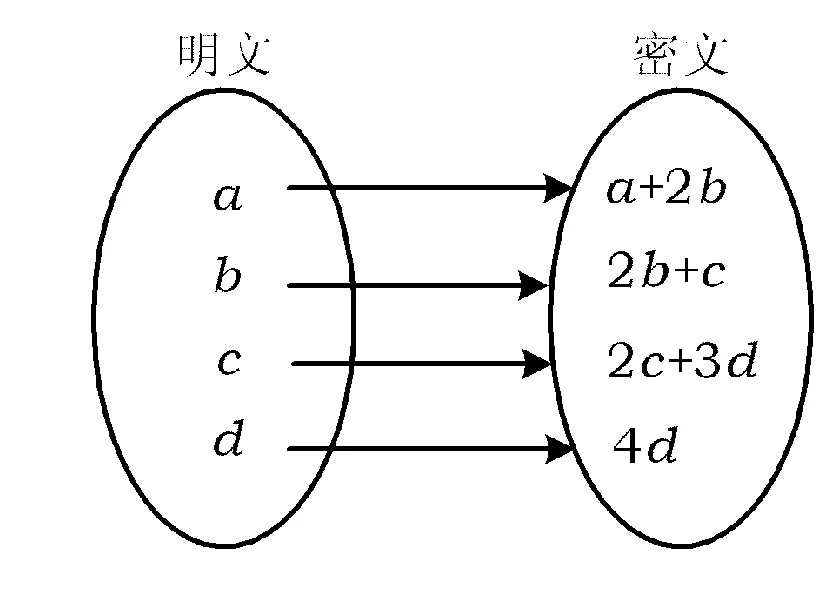
图5
赏析本题涉及到选修3-2中的信息安全与密码.当考生读懂题意后,运用方程思想列出4个线性方程,即可获解.题目中定义了一个新映射(如图5),即知道了象,求原象.由条件得
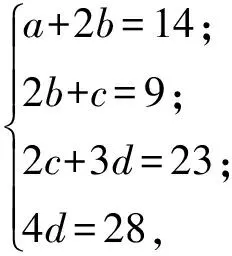
a=6,b=4,c=1,d=7.
故选C.
点评学生通过此题可初步了解情报或重要信息传输的原理和方法,体会信息安全与密码的重要作用.
3 以球面几何为背景
球面几何是一个重要的非欧几何的数学模型,它在大地测量、天体分析、航天航空、全球定位等方面有着广泛的应用.
( )
(2006年四川省数学高考理科试题)
赏析本题以球面几何中的余弦定理为背景.球面三角形ABC的3条边分别为
由球面三角形的余弦定理
cosa=cosbcosc+sinbsinccosA,
得
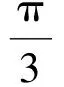
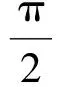
4 以“群”为背景
高等代数和近世代数是信息安全与密码的重要基础,它们在信息安全和网络技术中有着非常广泛的应用.
例7非空集合G关于运算⊕满足:(1)对任意a,b∈G,都有a⊕b∈G;(2)存在e∈G,使得对一切a∈G,都有a⊕e=e⊕a=a,则称G关于运算⊕为“融恰集”.现给出下列集合和运算:
①G={非负整数},⊕为整数的加法;
②G={偶数},⊕为整数的乘法;
③G={平面向量},⊕为平面向量的加法;
④G={二次三项式},⊕为多项式的加法;
⑤G={虚数},⊕为复数的乘法.
其中G关于运算⊕为“融恰集”的是________(写出所有“融恰集”的序号).
(2006年四川省数学高考理科试题)
赏析由定义知,“融洽集”满足2个条件:(1)G中任意2个元素经过运算⊕后结果还在G中,即非空集合G对运算⊕“封闭”;(2)集合G中存在一个“特殊元素”e.用方程的观点来看,条件(2)实质上是一个方程组,任意给出的a是否能解出e.下面分别判断这2个条件是否都成立.
①因为任意2个非负整数相加仍是非负整数,所以集合G对运算⊕“封闭”;又因为存在单位元e=0,使得对—切a∈G,都有a⊕e=e⊕a=a,所以G关于运算⊕为“融洽集”.
②因为集合G中不存在单位元,所以G关于运算⊕不是“融洽集”.
③因为集合G对运算⊕“封闭”,且存在一个单位元e=0满足条件,所以G关于运算⊕为“融洽集”.
④因为集合G对运算⊕“封闭”,但G中不存在单位元e,所以G关于运算⊕不是“融洽集”.
⑤因为2个虚数相乘可能为实数,所以集合G对运算⊕不“封闭”,故G关于运算⊕不是“融洽集”.
综上所述,G关于运算⊕为“融洽集”的是①,③.
点评本题以近世代数中群的定义为背景,主要考查学生的阅读理解能力、抽象与具体转化能力、方程思想、反例思想方法,是一道能有效地考查学生创新意识的好题目.
5 以“数域”为背景
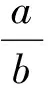
①整数集是数域;
②若有理数集Q⊆M,则数集M必为数域;
③数域必为无限集;
④存在无穷多个数域.
其中正确的命题序号是________(把你认为正确的命题序号填上).
(2008年福建省数学高考理科试题)
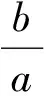
点评本题设计独特、背景深刻,具有很强的抽象性、发散性和创新性.这类以高等数学知识为背景的问题,能有效地考查学生进一步学习的潜质,已成为高考试题的一大亮点和热点,应予注意.
以选修系列3为背景的高考数学试题,具有立意鲜明、背景深刻、情境新颖、设计巧妙等特点,这些试题充分体现了《标准》的精神,它们对高中数学教师认真学习《标准》和实施高中数学课程改革具有良好的引领作用.
