圆锥曲线的又一个统一定值性质
2010-12-01
中学教研(数学) 2010年1期
●
(常德市第六中学 湖南常德 415003)
圆锥曲线的又一个统一定值性质
●彭世金
(常德市第六中学 湖南常德 415003)
文献[1]介绍了圆锥曲线的一个统一定值性质.笔者通过研究,又得到了圆锥曲线的另一个统一定值性质.
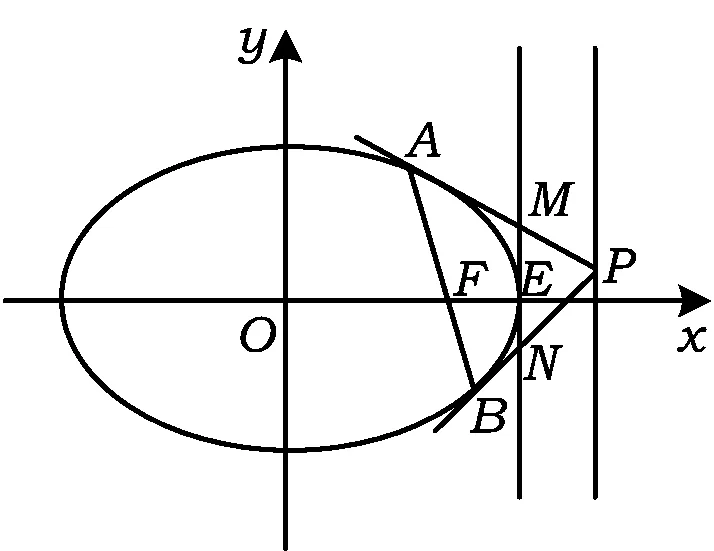
图1

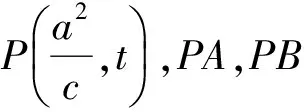
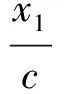
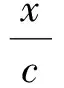
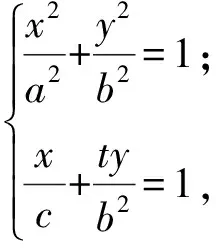
消去x得
(a2b2+t2c2)y2-2b2c2ty-b6=0.
由根与系数的关系得

于是
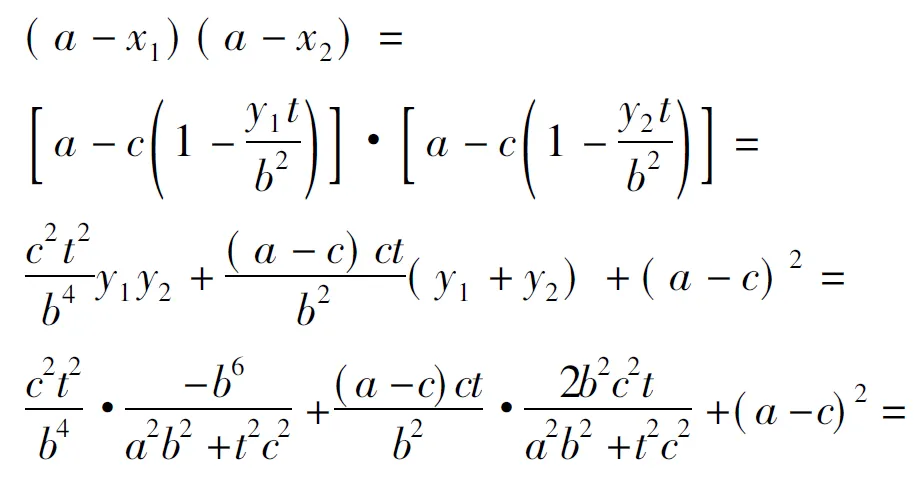
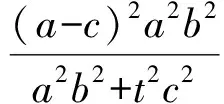
将椭圆在顶点E处的切线方程x=a与切线PA,PB的方程联立,可得点M,N的纵坐标分别为
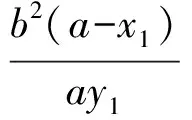
从而

类似地,双曲线与抛物线亦有如下定值性质.
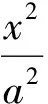
性质3如图3,已知抛物线y2=2px(p>0),F是抛物线的焦点,点E是抛物线的顶点,P是抛物线l的准线上任一点,抛物线的2条切线PA,PB与抛物线在顶点E处的切线分别相交于点M,N.记焦点F与顶点E的距离为d,则点M,N的纵坐标之积为定值-d2.
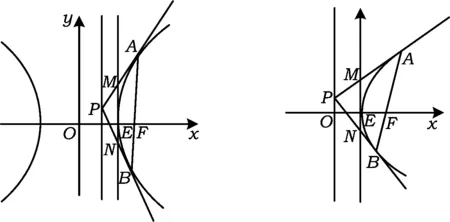
图2 图3
[1] 彭世金.圆锥曲线的一个统一定值性质[J].数学通讯:教师版,2009(7):24-25.
