如何用SAS软件正确分析生物医学科研资料VII.用SAS软件实现析因设计定量资料的统计分析

郭晋，胡良平，高辉，李长平

析因设计是生物医学科研资料中常见的一种定量资料实验设计类型，本文使用国际上著名的统计分析系统 SAS（statistical analysis system）软件对析因设计定量资料进行统计分析，分析实例均来自于生物学、医学领域，SAS 程序编写简明扼要，旨在迅速提高科研工作者使用 SAS 分析、处理生物医学科研资料的能力。

析因设计又称全因子实验设计，是在实验因素的个数≥ 2，各因素在实验中同时实施且所处的地位基本平等，因素之间存在一级、二级甚至更复杂的交互作用，且需要加以全面考察时所采用的一种多因素实验设计类型。这种设计要求将全部实验因素的水平进行全面组合，每种组合叫做一个实验点（或实验条件），在各实验点上要求至少做 2 次以上独立的重复实验。通常应将全部受试对象完全随机地均分入各实验条件所对应的组中。显然，该实验设计的实验次数很多，但可以对各因素之间各级交互作用的效应估计得比较准确。

当实验因素的个数不少于2个且各因素之间的各级交互作用不可忽视时，在研究者的时间、人力、经费等条件允许的情况下，应选用此设计。而当实验中所涉及的实验因素及其水平数非常多（实验因素个数大于6）、每次实验时间较长或花费较多时，不适宜选用此设计。

1 析因设计定量资料一元方差分析的SAS 实现

当实验按照析因设计安排，只有一个定量观测指标时，所得到的实验结果就称作析因设计一元定量资料。若资料满足独立性、正态性和方差齐性，则可以采用析因设计定量资料一元方差分析进行处理。例1 研究铜（Cu）和维生素 E（VE）对四氯化碳（CCl4）所致肝损伤的联合保护作用。实验动物为健康雄性 Wistar大鼠，共 60只，体重（190.2±25.3）g，随机均分为10组。VE组，VE 150 mg/kg 灌胃；Cu组，分 4个剂量组，即0.05、0.10、0.20、0.40 mg/kg（以 Cu 计）CuSO4·3H2O 灌胃；VE和Cu 联合组，分 4个剂量组，即 0.05、0.10、0.20、0.40 mg/kg（以 Cu 计）CuSO4·3H2O 分别与150 mg/kg VE共同灌胃；CCl4组，生理盐水灌胃。以上各组每天定时灌胃 1 次，连续 7 d，于第 8 天各组腹腔注射玉米油溶解的CCl4230 mg/kg，6 h 后断头处死，立即取血和肝脏，测定血清酶学指标 GPT和GOT、组织酶学指标 SOD。测得的SOD 数据如表1 所示，并假定资料满足参数检验的前提条件，试对资料进行统计分析[1]。

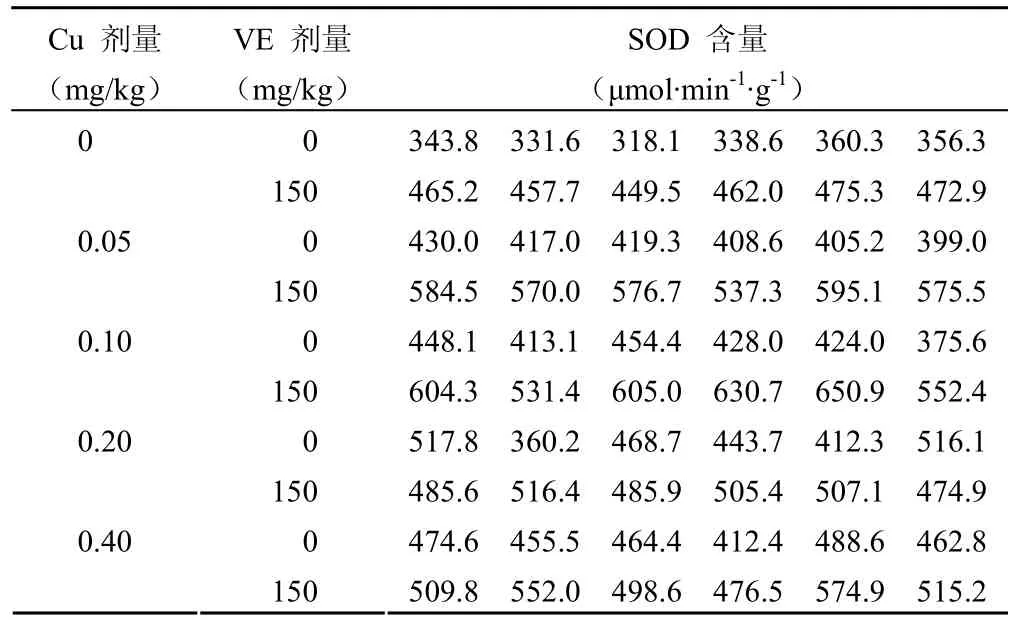
表1 Cu和VE 对 CCl4染毒大鼠肝脏 SOD的影响

分析与SAS：实现本研究确实涉及到 2个实验因素，即“Cu 剂量”和“VE 剂量”。“Cu 剂量”有 5个水平，即 0、0.05、0.10、0.20、0.40 mg/kg，“VE 剂量”有 2个水平，即 0、150 mg/kg，2个因素的各水平全面组合正好形成 10个组。又由于没有专业依据表明“Cu 剂量”和“VE剂量”对指标 SOD的影响哪一个是主要因素，且 2个因素同时作用于受试对象，因此本研究所对应的实验设计类型为两因素（或 5×2）析因设计。本研究观测指标只有一个，即“组织酶学指标 SOD”，假定数据满足各种参数检验所需要的前提条件，故可选用两因素（或 5×2）析因设计定量资料的一元方差分析对资料进行处理。

具体 SAS 程序：

DATA A1;DO Cu=0.00,0.05,0.10,0.20,0.40;DO VE=0,150;DO i=1 to 6;INPUT SOD @@; OUTPUT;END;END;END;CARDS;485.6516.4485.9505.4507.1474.9474.6455.5464.4412.4488.6462.8509.8552.0498.6476.5574.9515.2;RUN;Ods html;PROC GLM DATA=A1;

343.8331.6318.1338.6360.3356.3465.2457.7449.5462.0475.3472.9430.0417.0419.3408.6405.2399.0584.5570.0576.7537.3595.1575.5448.1413.1454.4428.0424.0375.6604.3531.4605.0630.7650.9552.4517.8360.2468.7443.7412.3516.1 CLASS CU VE;MODEL SOD=CU VE CU*VE / SS3;LSMEANS CU*VE / TDIFF PDIFF;RUN; QUIT;Ods html close;

SAS 输出结果与结果解释：

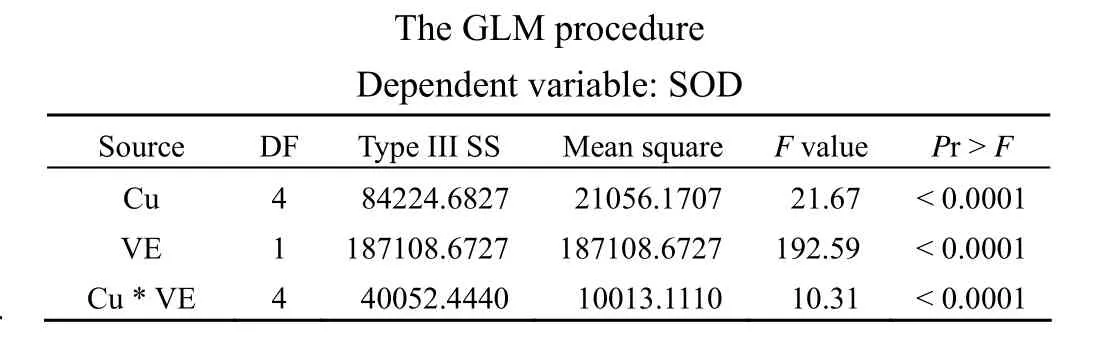
SAS 系统

以上是两因素析因设计定量资料的方差分析结果，可知Cu 剂量和VE 剂量对指标 SOD的影响都有统计学意义（F=21.67、P＜0.0001；F=192.59、P＜0.0001）；两因素之间的交互作用（Cu * VE）也有统计学意义（F=10.31、P＜0.0001）。

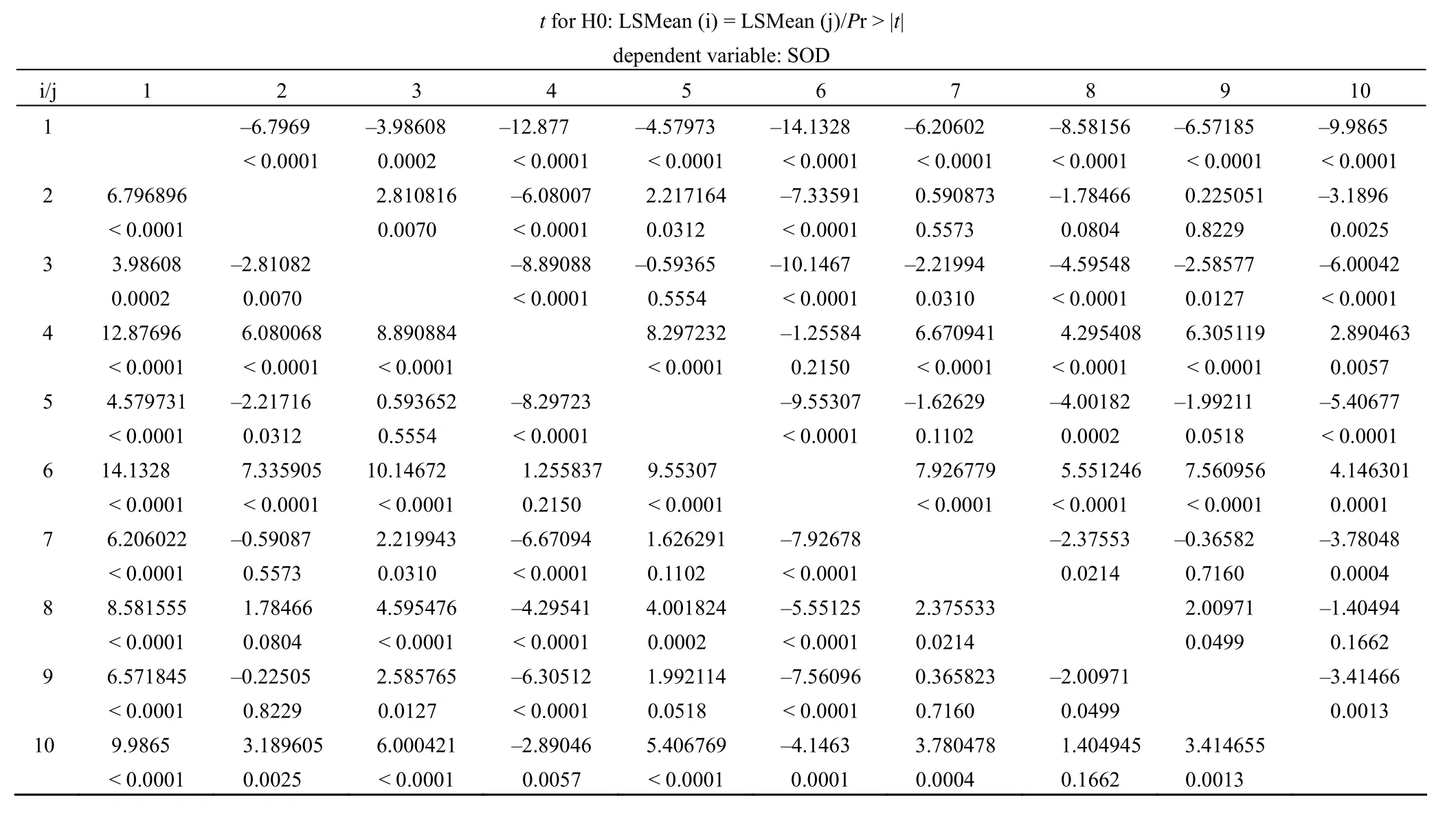
Least squares means for effect Cu * VE

以上是 10个均值之间两两比较的结果，横向与纵向的编号都是 1 ∼ 10号，横向与纵向交叉处就是相应的2个均值比较的结果，上行数值代表 t 统计量的数值，下行数值代表相应的概率 P 值。注意：此处“t 检验”的实质仍是方差分析，t 值平方就是方差分析中的F 值。

专业结论：Cu和VE 对 CCl4所致肝损伤大鼠肝脏的SOD 含量均有影响，且两者的影响具有相互联系。根据具体数据可以发现，在Cu 所取的5个水平上，VE 使用与否对 SOD 值影响较大，且均是使用 VE 各组的SOD 均值较高；在不用 VE 时，SOD 均值随 Cu 剂量的增加而增大，但在用 VE的情况下，Cu 剂量取 0.1 mg/kg 时 SOD均值最高。

分析表明：Cu和VE 对 CCl4所致肝损伤大鼠的肝脏具有联合保护作用，从本例的实验数据来看，当 Cu 剂量取 0.1 mg/kg、VE 剂量取 150 mg/kg 时 SOD 均值最高，保护效果最好。

2 析因设计定量资料多元方差分析的SAS 实现

对于析因设计定量资料，如果有 2个或以上观测指标在专业上存在相互联系或影响，对资料进行统计分析时需要同时予以考虑，则此时的统计分析方法就叫做析因设计定量资料的多元方差分析。

例2 调查某地 1981 — 1988年出生的近百名正常与肥胖儿童，按性别分别从两类儿童中各随机抽取 5 名，测定他们的5 项血脂指标，即 Y1（甘油三脂）、Y2（胆固醇）、Y3（低密度脂蛋白）、Y4（极低密度脂蛋白）、Y5（高密度脂蛋白），数据如下。假定数据满足参数检验的前提条件，试分析肥胖与否、性别及其交互作用对这 5 项观测指标的影响是否具有统计学意义[2]。

Y1 Y2 Y3 Y4 Y5正常男童： 32.04 169.86 144.53 24.78 31.6455.92 175.87 136.62 11.18 28.0755.15 138.02 101.04 11.03 25.9681.83 162.08 121.73 16.37 23.9865.43 155.00 112.42 13.09 29.88正常女童： 21.84 173.85 144.95 4.37 24.5350.16 192.68 156.19 10.03 26.46140.67 135.19 77.98 28.14 29.0837.35 172.46 143.80 6.33 22.33176.37 133.30 80.99 35.27 17.03肥胖男童： 28.57 170.75 146.62 5.71 18.4131.63 190.80 159.55 6.33 24.9241.43 148.48 110.89 8.27 29.3160.41 179.61 138.83 12.08 28.6970.05 174.80 127.45 14.01 32.54肥胖女童： 107.64 144.87 95.49 21.35 27.8571.83 121.26 53.37 14.37 53.5273.47 176.47 142.01 14.69 19.7676.59 142.30 70.73 15.32 56.2532.86 153.60 122.17 6.57 24.86

分析与SAS 实现：该资料涉及到 2个因素，一个为“儿童是否肥胖”，另一个为“儿童性别”。由于没有专业依据来判断“儿童是否肥胖”和“儿童性别”哪一个因素对结果变量的影响更为重要，所以认为两个因素对结果变量的影响同等重要，即认为两个因素的地位平等。因此本例资料所对应的实验设计类型为两因素（或 2×2）析因设计。

由于该资料涉及到 Y1（甘油三脂）、Y2（胆固醇）、Y3（低密度脂蛋白）、Y4（极低密度脂蛋白）、Y5（高密度脂蛋白）5个定量的结果变量，而且 5个结果变量在专业上明显存在着相互联系或影响，因此对资料进行统计分析时宜将这 5个结果变量同时予以考虑，进行多元统计分析。由于假定资料满足参数检验的前提条件，故对本例资料可采用两因素（或 2×2）析因设计五元定量资料的方差分析处理。

具体 SAS 程序：

DATA A2;DO FAT=1 TO 2;DO SEX=1 TO 2;DO REP=1 TO 5;INPUT Y1-Y5; OUTPUT;END; END; END;CARDS;32.04 169.86 144.53 24.78 31.6455.92 175.87 136.62 11.18 28.0755.15 138.02 101.04 11.03 25.9681.83 162.08 121.73 16.37 23.9865.43 155.00 112.42 13.09 29.8821.84 173.85 144.95 4.37 24.5350.16 192.68 156.19 10.03 26.46140.67 135.19 77.98 28.14 29.0837.35 172.46 143.80 6.33 22.33176.37 133.30 80.99 35.27 17.0328.57 170.75 146.62 5.71 18.4131.63 190.80 159.55 6.33 24.9241.43 148.48 110.89 8.27 29.3160.41 179.61 138.83 12.08 28.6970.05 174.80 127.45 14.01 32.54107.64 144.87 95.49 21.35 27.8571.83 121.26 53.37 14.37 53.5273.47 176.47 142.01 14.69 19.7676.59 142.30 70.73 15.32 56.2532.86 153.60 122.17 6.57 24.86;RUN;Ods html;PROC GLM DATA=A2;CLASS FAT SEX;MODEL Y1-Y5=FAT SEX FAT*SEX / SS3;MANOVA H=FAT SEX FAT*SEX;LSMEANS FAT*SEX / SLICE=FAT;LSMEANS FAT*SEX / SLICE=SEX;LSMEANS FAT*SEX / TDIFF PDIFF;RUN; QUIT;Ods html close;

SAS 输出结果与结果解释：

The GLM procedure Dependent variable: Y1

Dependent variable: Y2

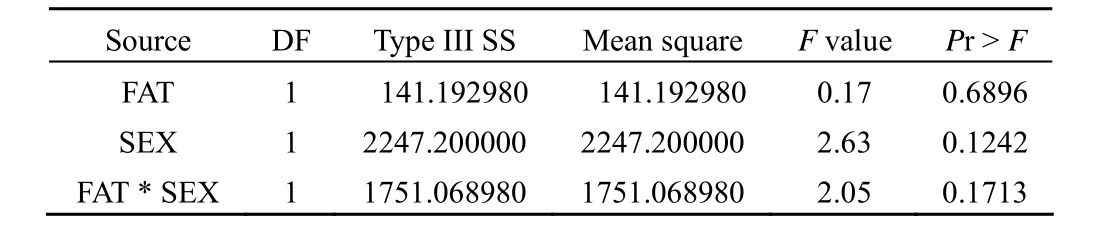
Dependent variable: Y3

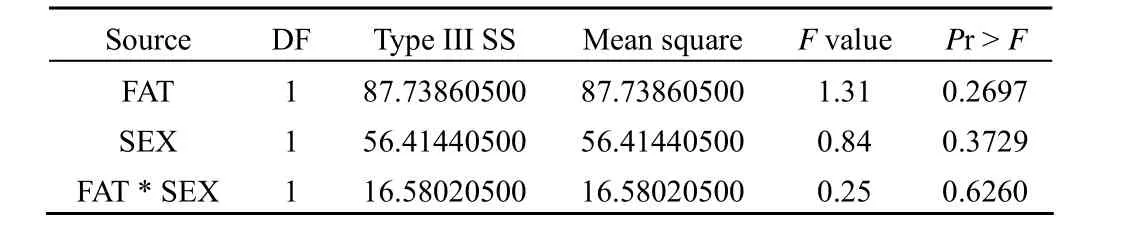
Dependent variable: Y4

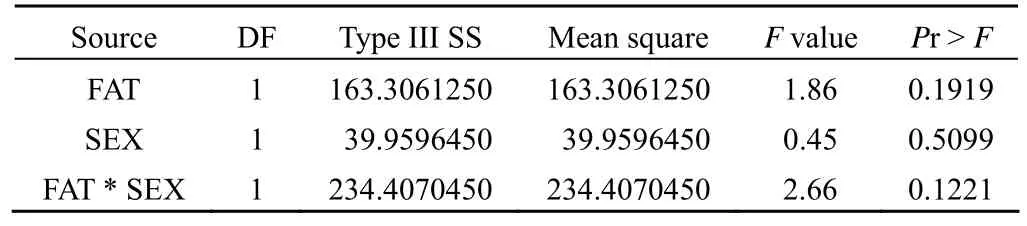
Dependent variable: Y5

以上是一元方差分析的结果，两实验因素及其交互作用对 5 项指标的影响均无统计学意义。

Multivariate analysis of variance

以上是多元方差分析的结果，两个因素及其交互作用对5 项指标整体的影响无统计学意义。

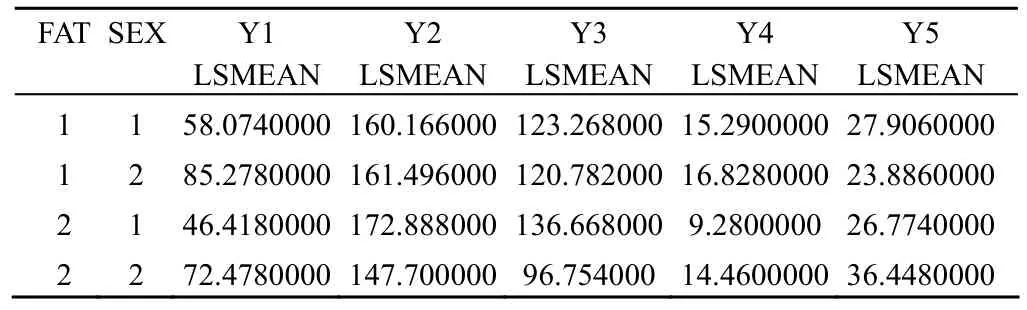
Least squares means

以上是两因素各水平组合下 5 项指标的校正均数。

专业结论：正常与肥胖儿童以及不同性别儿童的甘油三脂、胆固醇、低密度脂蛋白、极低密度脂蛋白、高密度脂蛋白指标检测结果差别不明显，需要注意的一个问题是，本例每个实验点下仅随机抽取了 5 例儿童进行各项指标的测量，所取的样本较小，加之个体之间这些指标的变异度较大，因此结论还需进一步实验验证。

[1]Hu LP.Medical statistics quantitative and qualitative data analysis using triple-type theory.Beijing: People's Military Medical Press,2009:131-135.(in Chinese)胡良平.医学统计学-运用三型理论分析定量与定性资料.北京:人民军医出版社, 2009:131-135.

[2]Hu LP.The practical course in the statistical analysis for windows SAS, version 6.12 & 8.0.Beijing: Press of Military Medical Sciences,2001:270-274.(in Chinese)胡良平.Windows SAS 6.12&8.0实用统计分析教程.北京: 军事医学科学出版社, 2001:270-274.